线性规划算法

news2024/9/22 19:43:30

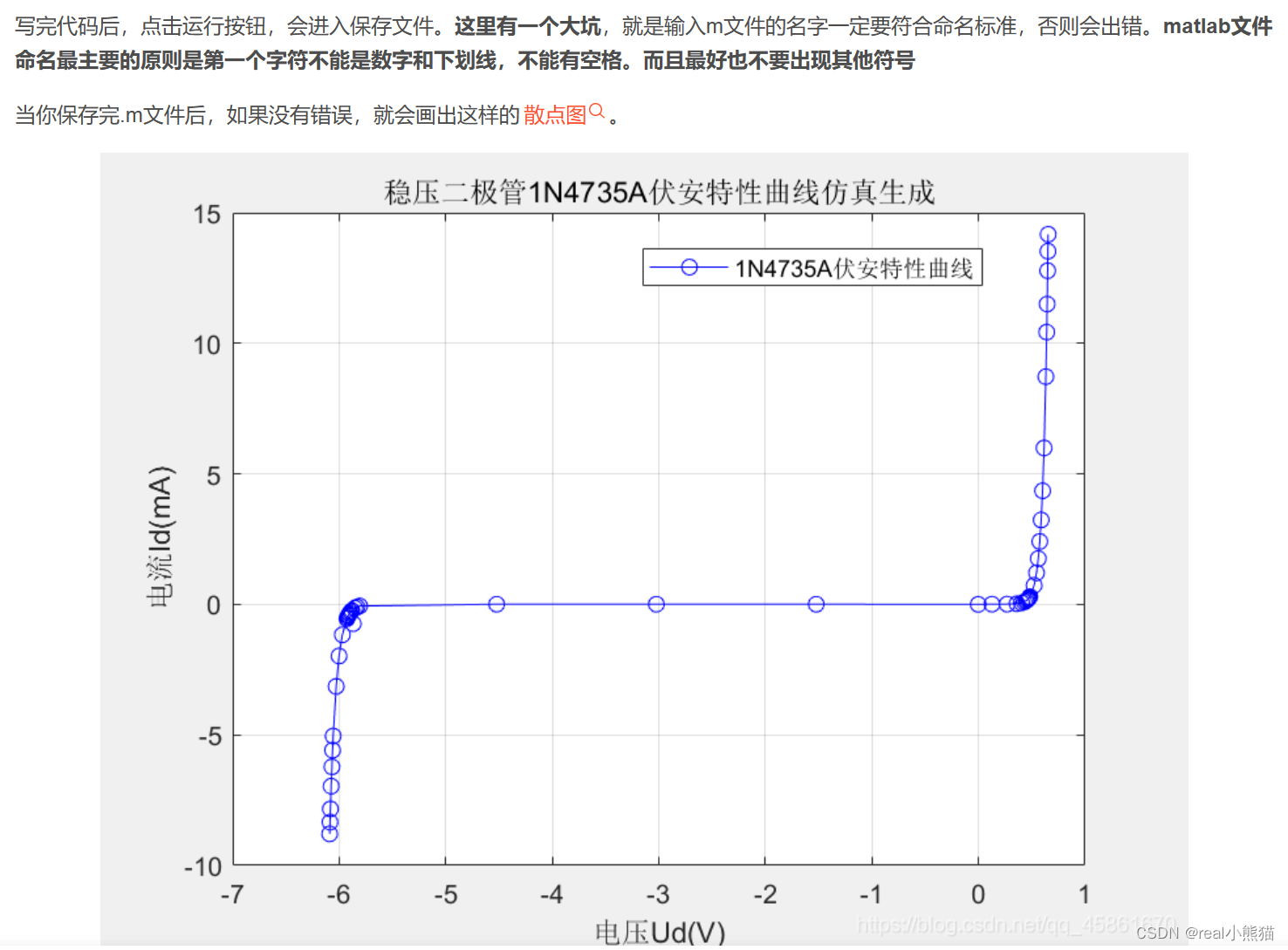
前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家：点击跳转

本文部分内容来自网友博客

一，线性规划

例如，一个企业“生产计划”的线性规划模型如下：

$max \, z = 50x_1+80x_2 \\ s.t. \, 0.5x_1 + 2x_2 \leq 40 \\ x_1+1.5x_2 \leq 45\\ x_1,x_2 \geq0$

$s.t.$ 是subject to的缩写，表示受限制于，其后跟约束条件。

线性规划问题三要素：

决策变量
目标函数
约束条件

线性规划问题的特点：

决策变量相互独立且连续变化
目标函数是线性函数
约束条件是线性不等式组

线性规划问题的解法：单纯形法、内点法

二，单纯形法

单纯形算法遵循“初始点——判优——改进”的优化模式。

1，基本概念

（1）线性规划的标准形式

满足如下四个条件的线性规划模型：

所有决策变量的取值是非负的；
除决策变量非负约束外的其他约束是等式约束；
模型中目标函数需要极大化（也可以要求极小化）；
等式约束中常数项位于等号的右端（称为右端项，right hand side）

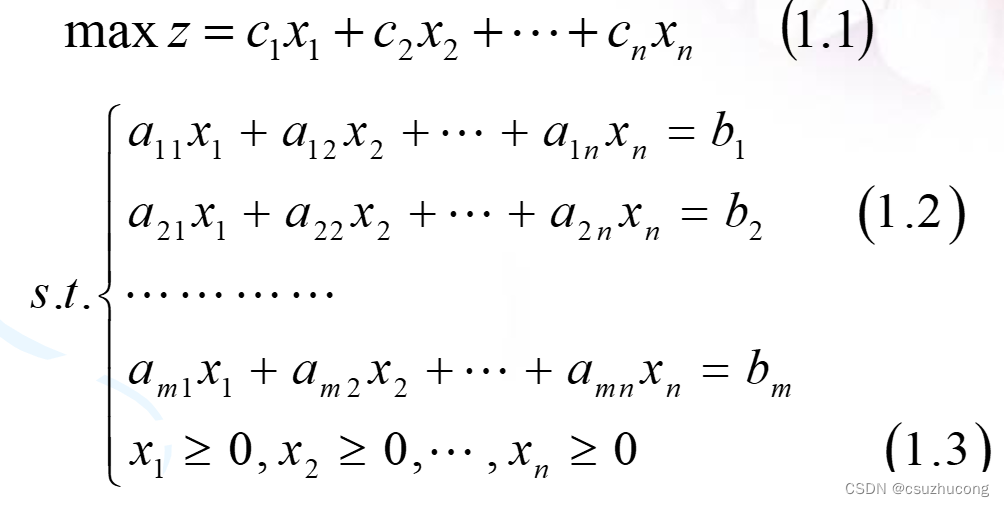
（2）线性规划的典范形式

典范形式是标准形式的基础上，额外满足：

右端项是非负的；
在等式约束中存在一组与等式约束个数相等的决策变量，它们的系数构成系数矩阵的一个单位子矩阵。

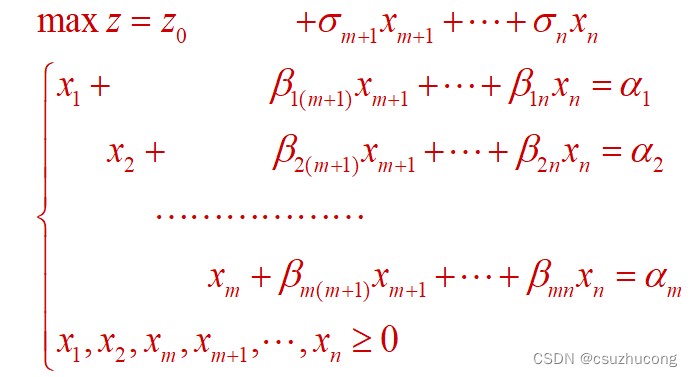
其中Z0是可行解（常数），因为有等式，所以max z的式子里面可以把x1 - xm都替换掉。

（3）线性规划的可行域

线性规划的可行域是一个多面体，但可能是无界的。

若多面体S={x|Ax=b,x≥0}是非空的，则必存在极点。

（4）线性规划基本定理、问题转化

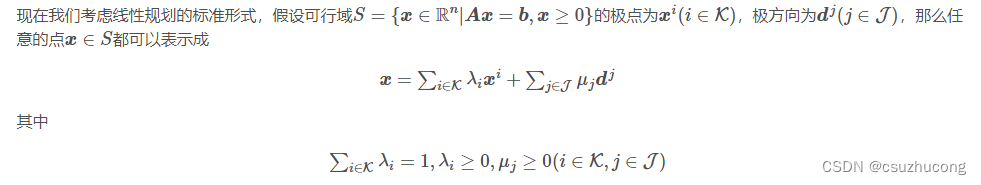
极点、极向量参考凸优化

于是线性规划可以表示成只有一个等式约束和若干个非负变量约束的线性规划问题：

${\rm min} \sum_{i \in \mathcal{K}}(\boldsymbol{c}^{\rm T} \boldsymbol{x}^i) \lambda_i + \sum_{j \in \mathcal{J}}(\boldsymbol{c}^{\rm T} \boldsymbol{d}^j) \mu_j , \\ {\rm s.t.} \sum_{i \in \mathcal{K}} \lambda_i = 1, \\ \lambda_i \geq 0, \mu_j \geq 0, i \in \mathcal{K} , j \in \mathcal{J}.$

这又分为2种情形：

于是极小化问题可转化为：

${\rm min} \sum_{i \in \mathcal{K}}(\boldsymbol{c}^{\rm T} \boldsymbol{x}^i) \lambda_i, \\ {\rm s.t.} \sum_{i \in \mathcal{K}} \lambda_i =1, \lambda_i \geq 0, i \in \mathcal{K}.$

转化后的问题，可行域是一个有限多面体，最优值一定在某个λi=1时取到。

2，寻找初始点

确定单纯形算法初始点的策略：两阶段法、大M法

3，判优规则

线性规划典范形式的矩阵表达式:

${\rm min} z=\boldsymbol{c}_{\boldsymbol{B}}^{\rm T}\boldsymbol{B}^{-1}\boldsymbol{b} + (\boldsymbol{c}_{\boldsymbol{N}}^{\rm T}-\boldsymbol{c}_{\boldsymbol{B}}^{\rm T}\boldsymbol{B}^{-1}\boldsymbol{N}) \boldsymbol{x}_{\boldsymbol{N}} \\ {\rm s.t.} \boldsymbol{x}_{\boldsymbol{B}}+\boldsymbol{B}^{-1}\boldsymbol{N}\boldsymbol{x}_{\boldsymbol{N}}=\boldsymbol{B}^{-1}\boldsymbol{b}, \boldsymbol{x}_{\boldsymbol{B}} \geq 0, \boldsymbol{x}_{\boldsymbol{N}} \geq 0.$

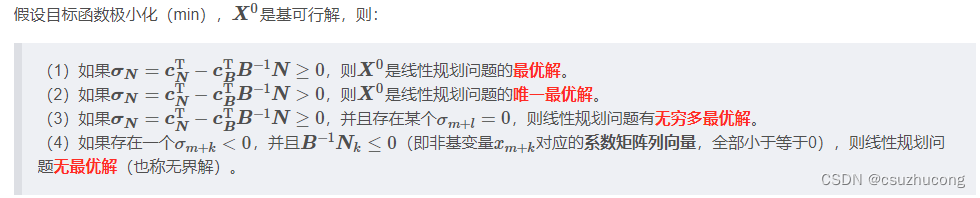
4，改进规则

一个转轴过程可以分成三个部分：

（1）确定进入可行基的非基变量（称为转入规则（pivoting in））;

（2）确定离开可行基的基变量（称为转出规则（pivoting out））;

（3）进行可行基转换的线性方程组Gauss消去操作（称为转轴操作）。

三，对偶单纯形法

待补充

四，原始对偶算法

待补充

五，内点法

单纯形算法虽然在实际应用中非常有效，至今占有绝对优势，但在理论上它还不是多项式算法。
1979年，前苏联数学家第一个给出了求解线性规划的多项式算法，这就是所谓的椭球算法。这个算法在理论上是重要的，但是计算结果很不理想，远不及单纯形方法有效。
人们提出进一步的问题：能否找到实用上也确实有效的多项式时间算法？正是在这样的背景下，产生了内点法。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/713864.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！