小时候有时间就很喜欢趁着下课放学的时间去抓蝴蝶玩,五彩多样的蝴蝶让人应接不暇,现在早就过了那个天真玩耍的年纪了,如今看到蝴蝶的第一反应就是这是什么蝴蝶,没有专业的知识支撑很难识别出来具体的种类,本文的主要目的就是想要基于深度学习目标检测模型来尝试开发构建蝴蝶细粒度目标检测识别模型,首先看小效果图,如下所示:
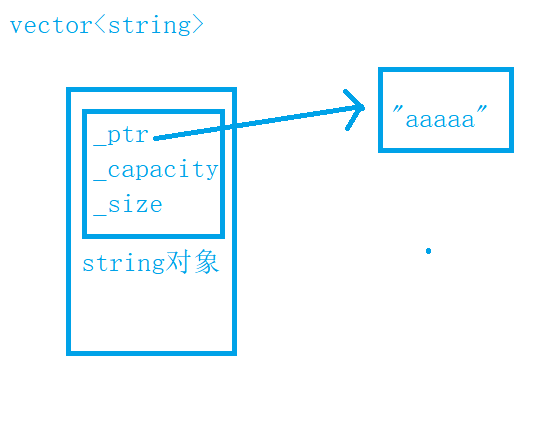
接下来看下我准备的数据集,一共收集到了20种不同类别的蝴蝶图像数据集,之后人工标注数据得到所需要的数据集。

以下是20种蝴蝶的信息解释:
-
Atrophaneura_horishanus: 科学名称为Atrophaneura horishanus,属于阿特罗法尼乌拉亚属(Atrophaneura),可能是一种热带地区的蝴蝶。
-
Atrophaneura_varuna: 科学名称为Atrophaneura varuna,同样属于阿特罗法尼乌拉亚属(Atrophaneura),可能是另一种热带地区的蝴蝶。
-
Byasa_alcinous: 科学名称为Byasa alcinous,属于拟鳞蛱蝶属(Byasa),可能是一种大型的蛱蝶,分布在某些地区。
-
Byasa_dasarada: 科学名称为Byasa dasarada,同样属于拟鳞蛱蝶属(Byasa),可能是另一种大型的蛱蝶,具有特定的地理分布。
-
Byasa_polyeuctes: 科学名称为Byasa polyeuctes,仍然属于拟鳞蛱蝶属(Byasa),可能是另一种大型的蛱蝶,具有不同的特征和分布。
-
Graphium_agamemnon: 科学名称为Graphium agamemnon,属于凤蝶属(Graphium),可能是一种美丽的凤蝶,具有独特的花纹和颜色。
-
Graphium_cloanthus: 科学名称为Graphium cloanthus,同样属于凤蝶属(Graphium),可能是另一种引人注目的凤蝶,分布在某些地区。
-
Graphium_sarpedon: 科学名称为Graphium sarpedon,仍然属于凤蝶属(Graphium),可能是另一种迷人的凤蝶,栖息于特定的地理区域。
-
Iphiclides_podalirius: 科学名称为Iphiclides podalirius,属于斑蝶属(Iphiclides),可能是一种优雅的斑蝶,具有独特的外观和分布。
-
Lamproptera_curius: 科学名称为Lamproptera curius,属于亮蛱蝶属(Lamproptera),可能是一种光彩夺目的蛱蝶,展示出令人惊叹的色彩。
-
Lamproptera_meges: 科学名称为Lamproptera meges,同样属于亮蛱蝶属(Lamproptera),可能是另一种华丽的蛱蝶,有着不同的特点和分布。
-
Losaria_coon: 科学名称为Losaria coon,属于斑尺蛾属(Losaria),可能是一种斑尺蛾,具有独特的形态和分布。
-
Meandrusa_payeni: 科学名称为Meandrusa payeni,属于猫眼蝶属(Meandrusa),可能是一种稀有的猫眼蝶,栖息在某些特定的地区。
-
Meandrusa_sciron: 科学名称为Meandrusa sciron,同样属于猫眼蝶属(Meandrusa),可能是另一种美丽的猫眼蝶,具有不同的特征和分布。
-
Pachliopta_aristolochiae: 科学名称为Pachliopta aristolochiae,属于斗羽蝶属(Pachliopta),可能是一种特殊的斗羽蝶,以其对防御性植物毒素的耐受能力而闻名。
-
Papilio_alcmenor: 科学名称为Papilio alcmenor,属于大鳞尾属(Papilio),可能是一种大型的鳞尾蝶,具有独特的翅膀形态和花纹。
-
Papilio_arcturus: 科学名称为Papilio arcturus,同样属于大鳞尾属(Papilio),可能是另一种引人注目的鳞尾蝶,栖息于特定的地理区域。
-
Papilio_bianor: 科学名称为Papilio bianor,仍然属于大鳞尾属(Papilio),可能是另一种迷人的鳞尾蝶,具有不同的特征和分布。
-
Papilio_dialis: 科学名称为Papilio dialis,属于大鳞尾属(Papilio),可能是一种华丽的鳞尾蝶,展示出令人惊叹的色彩以及翅膀上的花纹。
-
Papilio_hermosanus: 科学名称为Papilio hermosanus,同样属于大鳞尾属(Papilio),可能是一种壮丽的鳞尾蝶,有着不同的特点和分布。
详细对应信息如下所示:
{
"0": "Atrophaneura_horishanus",
"1": "Atrophaneura_varuna",
"2": "Byasa_alcinous",
"3": "Byasa_dasarada",
"4": "Byasa_polyeuctes",
"5": "Graphium_agamemnon",
"6": "Graphium_cloanthus",
"7": "Graphium_sarpedon",
"8": "Iphiclides_podalirius",
"9": "Lamproptera_curius",
"10": "Lamproptera_meges",
"11": "Losaria_coon",
"12": "Meandrusa_payeni",
"13": "Meandrusa_sciron",
"14": "Pachliopta_aristolochiae",
"15": "Papilio_alcmenor",
"16": "Papilio_arcturus",
"17": "Papilio_bianor",
"18": "Papilio_dialis",
"19": "Papilio_hermosanus"
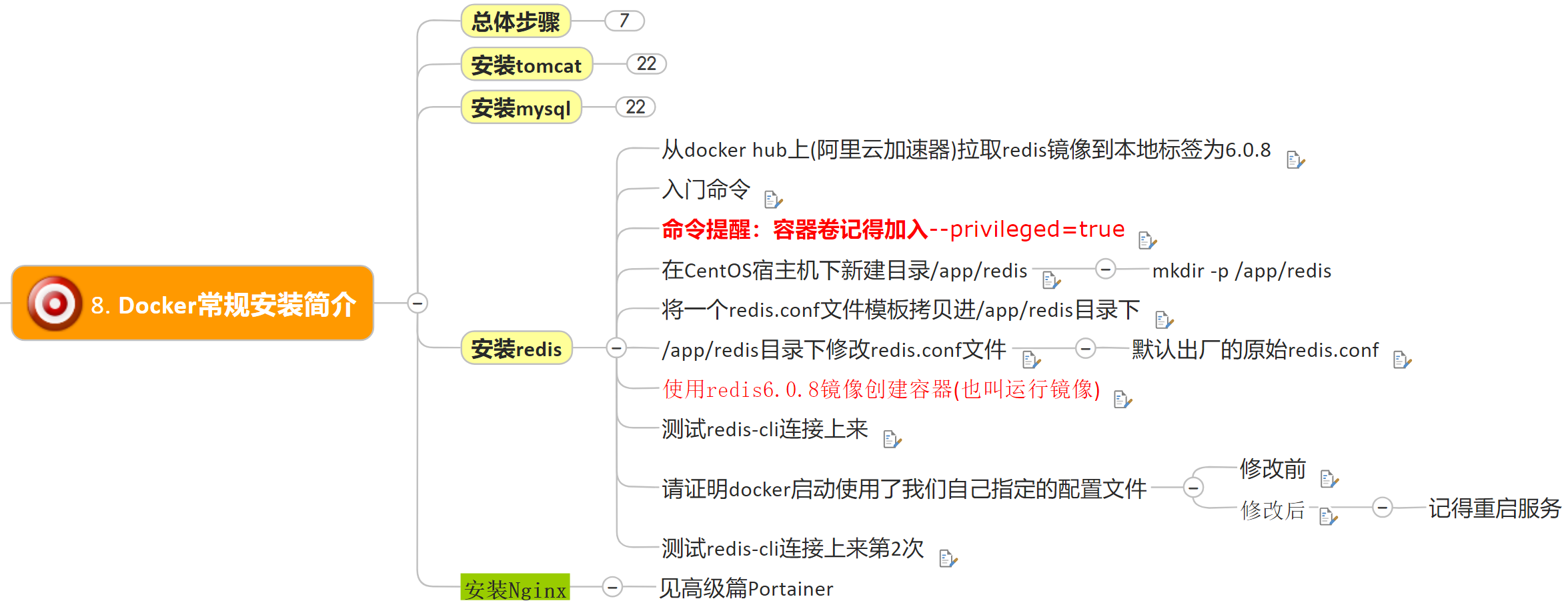
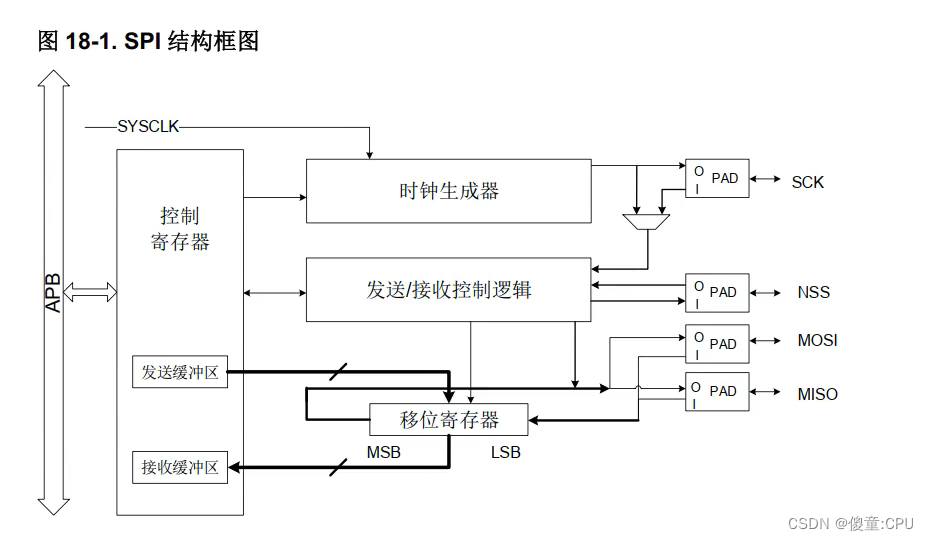
}这里我选用的模型是yolov5s系列的模型,如下所示:
# YOLOv5 🚀 by Ultralytics, GPL-3.0 license
# Parameters
nc: 20 # number of classes
depth_multiple: 0.33 # model depth multiple
width_multiple: 0.50 # layer channel multiple
anchors:
- [10,13, 16,30, 33,23] # P3/8
- [30,61, 62,45, 59,119] # P4/16
- [116,90, 156,198, 373,326] # P5/32
#Backbone
backbone:
# [from, number, module, args]
[[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2
[-1, 1, Conv, [128, 3, 2]], # 1-P2/4
[-1, 3, C3, [128]],
[-1, 1, Conv, [256, 3, 2]], # 3-P3/8
[-1, 6, C3, [256]],
[-1, 1, Conv, [512, 3, 2]], # 5-P4/16
[-1, 9, C3, [512]],
[-1, 1, Conv, [1024, 3, 2]], # 7-P5/32
[-1, 3, C3, [1024]],
[-1, 1, SPPF, [1024, 5]], # 9
]
#Head
head:
[[-1, 1, Conv, [512, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 6], 1, Concat, [1]], # cat backbone P4
[-1, 3, C3, [512, False]], # 13
[-1, 1, Conv, [256, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 4], 1, Concat, [1]], # cat backbone P3
[-1, 3, C3, [256, False]], # 17 (P3/8-small)
[-1, 1, Conv, [256, 3, 2]],
[[-1, 14], 1, Concat, [1]], # cat head P4
[-1, 3, C3, [512, False]], # 20 (P4/16-medium)
[-1, 1, Conv, [512, 3, 2]],
[[-1, 10], 1, Concat, [1]], # cat head P5
[-1, 3, C3, [1024, False]], # 23 (P5/32-large)
[[17, 20, 23], 1, Detect, [nc, anchors]], # Detect(P3, P4, P5)
]
默认100次epoch的迭代计算,计算日志输出如下所示:
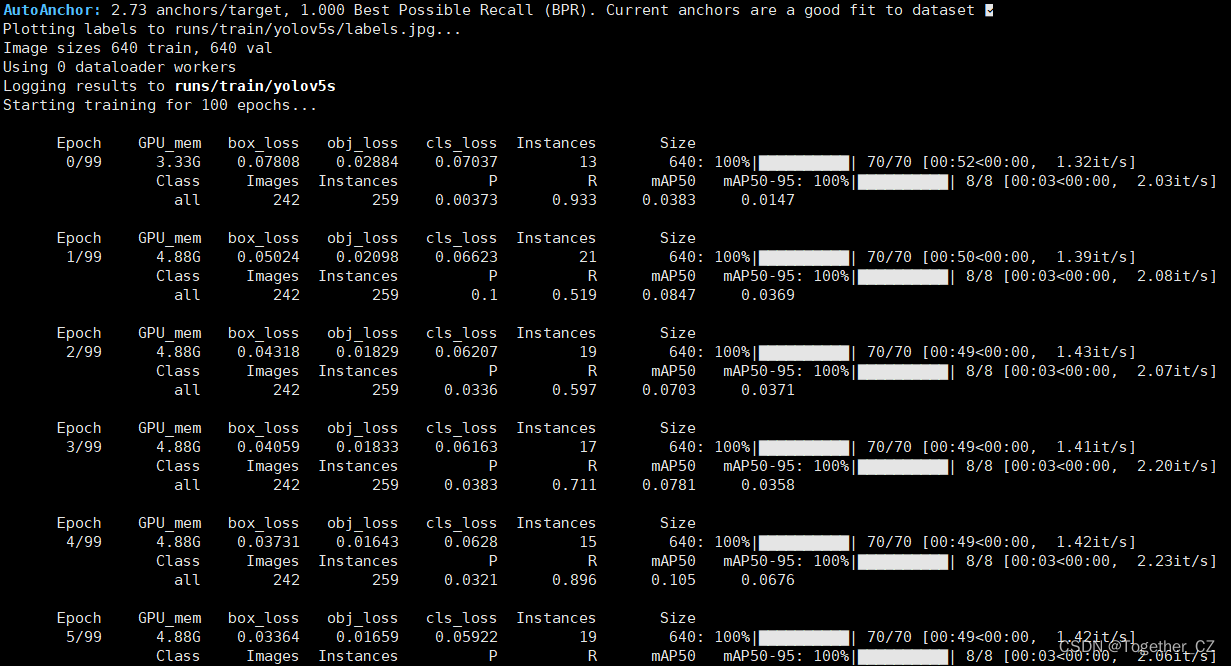
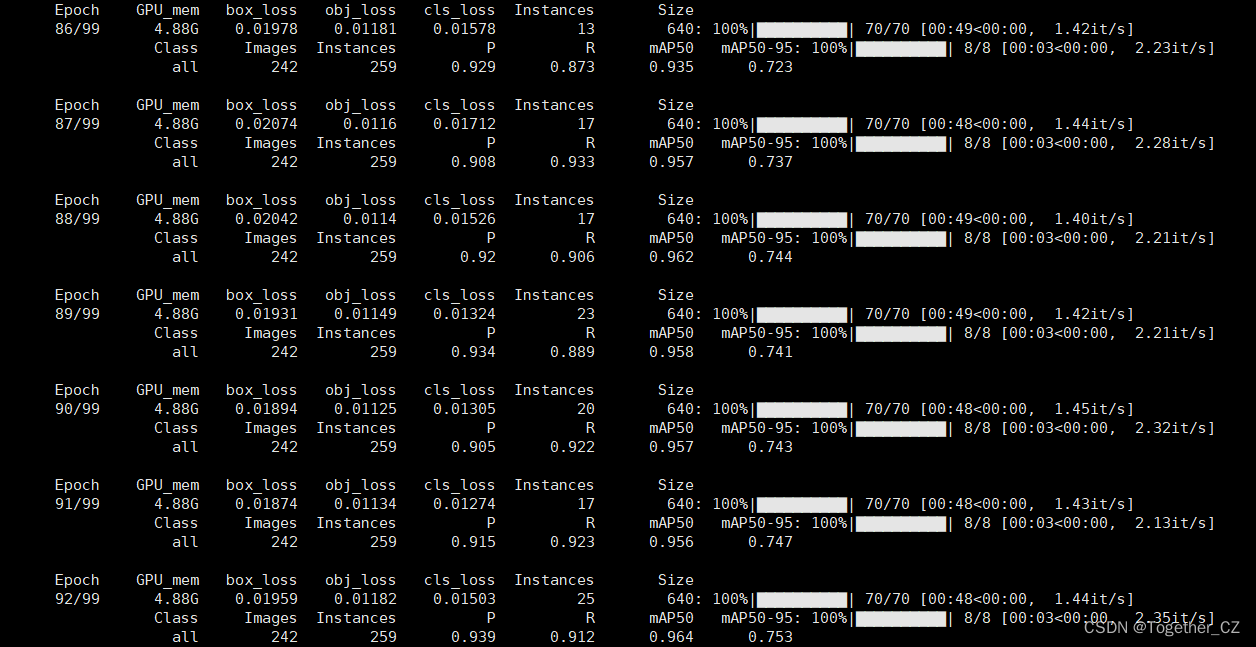
模型训练完成后对模型进行评估计算,如下所示:
Validating runs/train/yolov5s/weights/best.pt...
Fusing layers...
YOLOv5s summary: 157 layers, 7064065 parameters, 0 gradients, 15.9 GFLOPs
Class Images Instances P R mAP50 mAP50-95: 100%|??????????| 8/8 [00:04<00:00, 1.64it/s]
all 242 259 0.942 0.904 0.965 0.756
Atrophaneura_horishanus 242 8 0.964 1 0.995 0.762
Atrophaneura_varuna 242 7 1 0.89 0.995 0.839
Byasa_alcinous 242 18 0.888 1 0.989 0.767
Byasa_dasarada 242 15 0.822 0.733 0.887 0.707
Byasa_polyeuctes 242 16 0.924 0.762 0.902 0.722
Graphium_agamemnon 242 10 0.929 1 0.995 0.849
Graphium_cloanthus 242 20 1 0.919 0.971 0.731
Graphium_sarpedon 242 6 0.811 1 0.901 0.726
Iphiclides_podalirius 242 16 0.986 1 0.995 0.764
Lamproptera_curius 242 13 0.976 0.769 0.876 0.612
Lamproptera_meges 242 20 1 0.809 0.981 0.62
Losaria_coon 242 11 1 0.842 0.995 0.795
Meandrusa_payeni 242 8 0.987 1 0.995 0.738
Meandrusa_sciron 242 9 1 0.938 0.995 0.759
Pachliopta_aristolochiae 242 19 1 0.767 0.96 0.732
Papilio_alcmenor 242 11 0.899 1 0.995 0.861
Papilio_arcturus 242 14 0.988 0.857 0.966 0.856
Papilio_bianor 242 11 0.885 1 0.98 0.84
Papilio_dialis 242 16 0.877 0.892 0.949 0.748
Papilio_hermosanus 242 11 0.895 0.909 0.973 0.698
Results saved to runs/train/yolov5s
接下来看下具体的指标详情,如下所示:
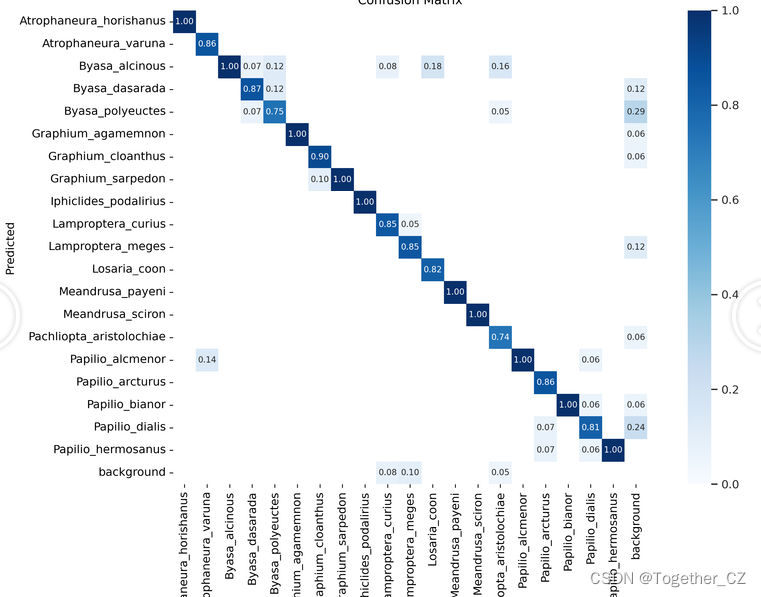
【混淆矩阵】
混淆矩阵(Confusion Matrix)是在机器学习领域中常用的评估分类模型性能的工具。它以矩阵的形式展示了分类模型预测结果与实际标签之间的差异。
混淆矩阵包括四个关键术语:
- 真正例(True Positive, TP):模型正确地将正例预测为正例。
- 假正例(False Positive, FP):模型错误地将负例预测为正例。
- 假反例(False Negative, FN):模型错误地将正例预测为负例。
- 真反例(True Negative, TN):模型正确地将负例预测为负例。
混淆矩阵的一般形式如下:
预测正例 预测负例
实际正例 TP FN
实际负例 FP TN
可以根据混淆矩阵的内容计算许多有用的评估指标,例如:
- 准确率(Accuracy):分类正确的样本占总样本数的比例,计算公式为
(TP + TN) / (TP + TN + FP + FN)。 - 精确率(Precision):预测为正例的样本中真实为正例的比例,计算公式为
TP / (TP + FP)。 - 召回率(Recall):真实为正例的样本中被正确预测为正例的比例,计算公式为
TP / (TP + FN)。 - F1分数(F1 Score):精确率和召回率的综合评估指标,计算公式为
2 * (Precision * Recall) / (Precision + Recall)。
混淆矩阵可用于直观地理解分类模型在不同类别上的性能,并帮助确定是否存在误分类的情况。根据具体应用场景,可以选择适当的评估指标来衡量分类模型的效果。
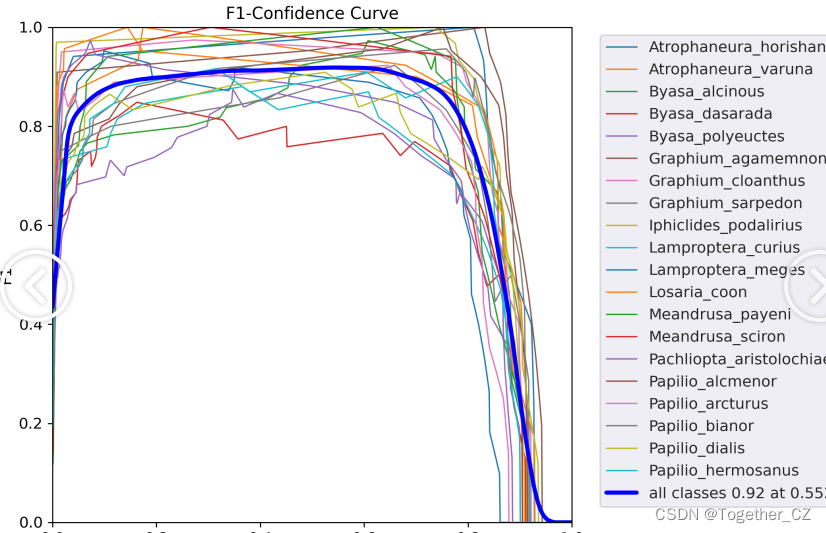
【F1值曲线】
F1值曲线是一种用于评估二分类模型在不同阈值下的性能的可视化工具。它通过绘制不同阈值下的精确率(Precision)、召回率(Recall)和F1分数的关系图来帮助我们理解模型的整体性能。
F1分数是精确率和召回率的调和平均值,它综合考虑了两者的性能指标。F1值曲线可以帮助我们确定在不同精确率和召回率之间找到一个平衡点,以选择最佳的阈值。
绘制F1值曲线的步骤如下:
- 使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
- 对于每个阈值,计算相应的精确率、召回率和F1分数。
- 将每个阈值下的精确率、召回率和F1分数绘制在同一个图表上,形成F1值曲线。
- 根据F1值曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
F1值曲线通常与接收者操作特征曲线(ROC曲线)一起使用,以帮助评估和比较不同模型的性能。它们提供了更全面的分类器性能分析,可以根据具体应用场景来选择合适的模型和阈值设置。
【Precision曲线】
精确率曲线(Precision-Recall Curve)是一种用于评估二分类模型在不同阈值下的精确率性能的可视化工具。它通过绘制不同阈值下的精确率和召回率之间的关系图来帮助我们了解模型在不同阈值下的表现。
精确率(Precision)是指被正确预测为正例的样本数占所有预测为正例的样本数的比例。召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。
绘制精确率曲线的步骤如下:
- 使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
- 对于每个阈值,计算相应的精确率和召回率。
- 将每个阈值下的精确率和召回率绘制在同一个图表上,形成精确率曲线。
- 根据精确率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察精确率曲线,我们可以根据需求确定最佳的阈值,以平衡精确率和召回率。较高的精确率意味着较少的误报,而较高的召回率则表示较少的漏报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
精确率曲线通常与召回率曲线(Recall Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。

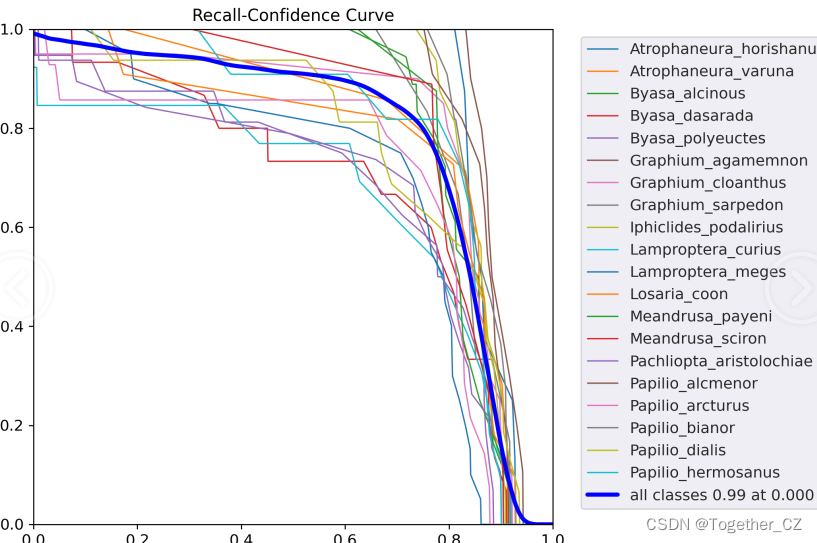
【召回率曲线】
召回率曲线(Recall Curve)是一种用于评估二分类模型在不同阈值下的召回率性能的可视化工具。它通过绘制不同阈值下的召回率和对应的精确率之间的关系图来帮助我们了解模型在不同阈值下的表现。
召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。召回率也被称为灵敏度(Sensitivity)或真正例率(True Positive Rate)。
绘制召回率曲线的步骤如下:
- 使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
- 对于每个阈值,计算相应的召回率和对应的精确率。
- 将每个阈值下的召回率和精确率绘制在同一个图表上,形成召回率曲线。
- 根据召回率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察召回率曲线,我们可以根据需求确定最佳的阈值,以平衡召回率和精确率。较高的召回率表示较少的漏报,而较高的精确率意味着较少的误报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
召回率曲线通常与精确率曲线(Precision Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
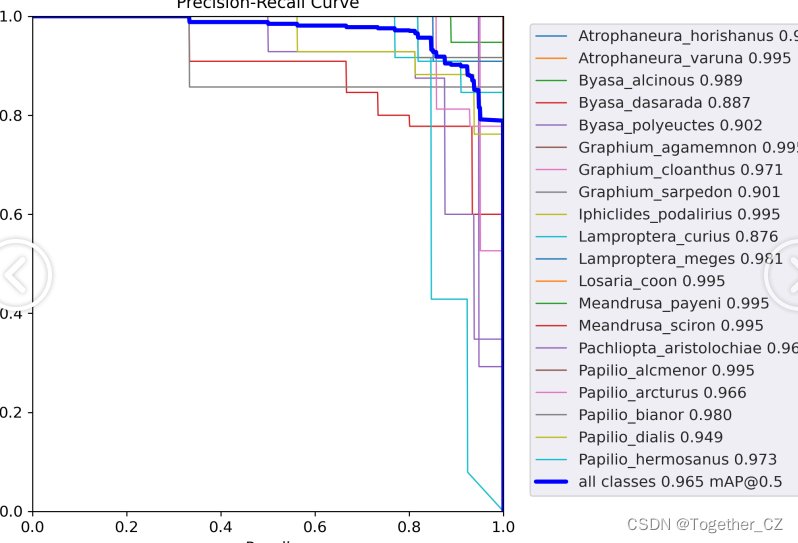
【PR曲线】
精确率-召回率曲线(Precision-Recall Curve)是一种用于评估二分类模型性能的可视化工具。它通过绘制不同阈值下的精确率(Precision)和召回率(Recall)之间的关系图来帮助我们了解模型在不同阈值下的表现。
精确率是指被正确预测为正例的样本数占所有预测为正例的样本数的比例。召回率是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。
绘制精确率-召回率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率和召回率。
将每个阈值下的精确率和召回率绘制在同一个图表上,形成精确率-召回率曲线。
根据曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
精确率-召回率曲线提供了更全面的模型性能分析,特别适用于处理不平衡数据集和关注正例预测的场景。曲线下面积(Area Under the Curve, AUC)可以作为评估模型性能的指标,AUC值越高表示模型的性能越好。
通过观察精确率-召回率曲线,我们可以根据需求选择合适的阈值来权衡精确率和召回率之间的平衡点。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
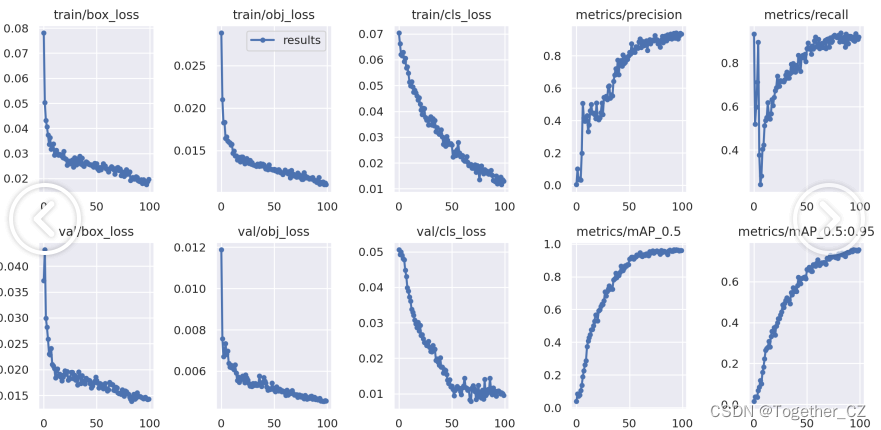
模型训练过程可视化如下所示:
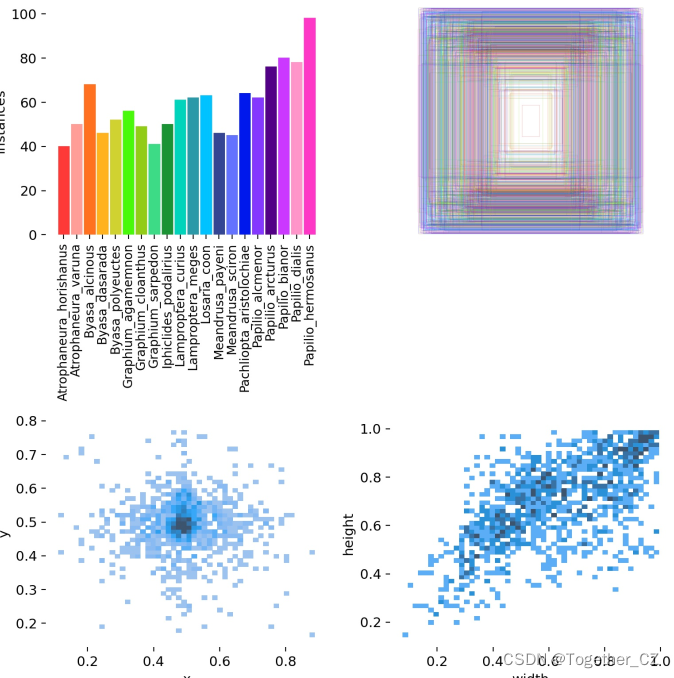
【数据类别标签可视化】如下所示:
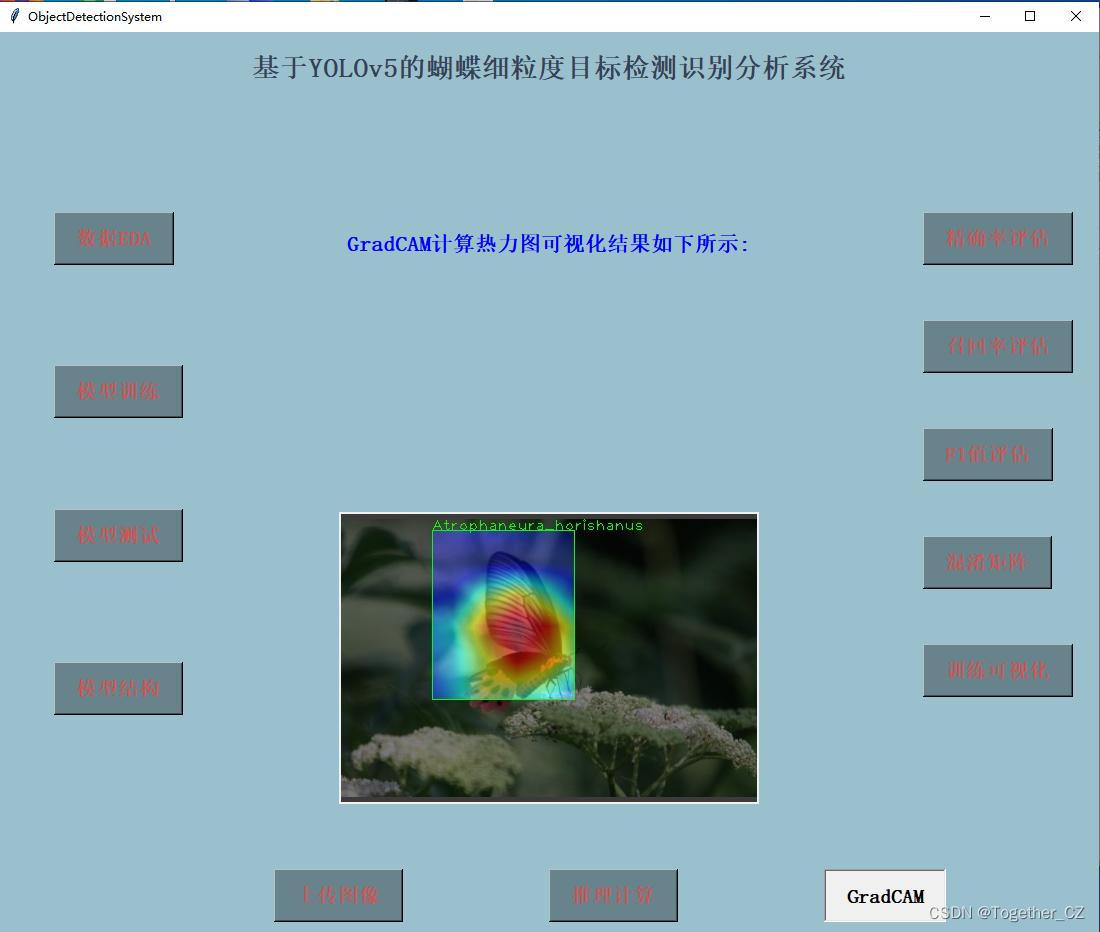
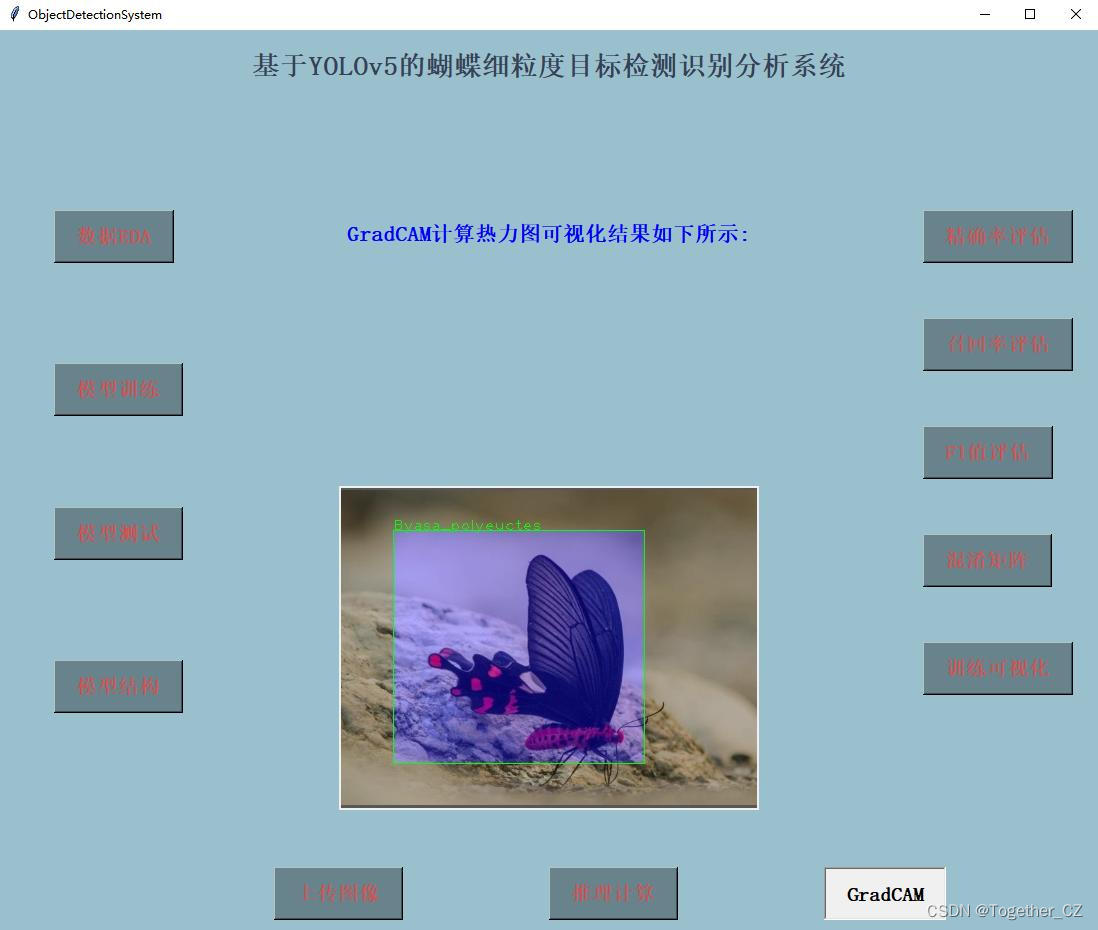
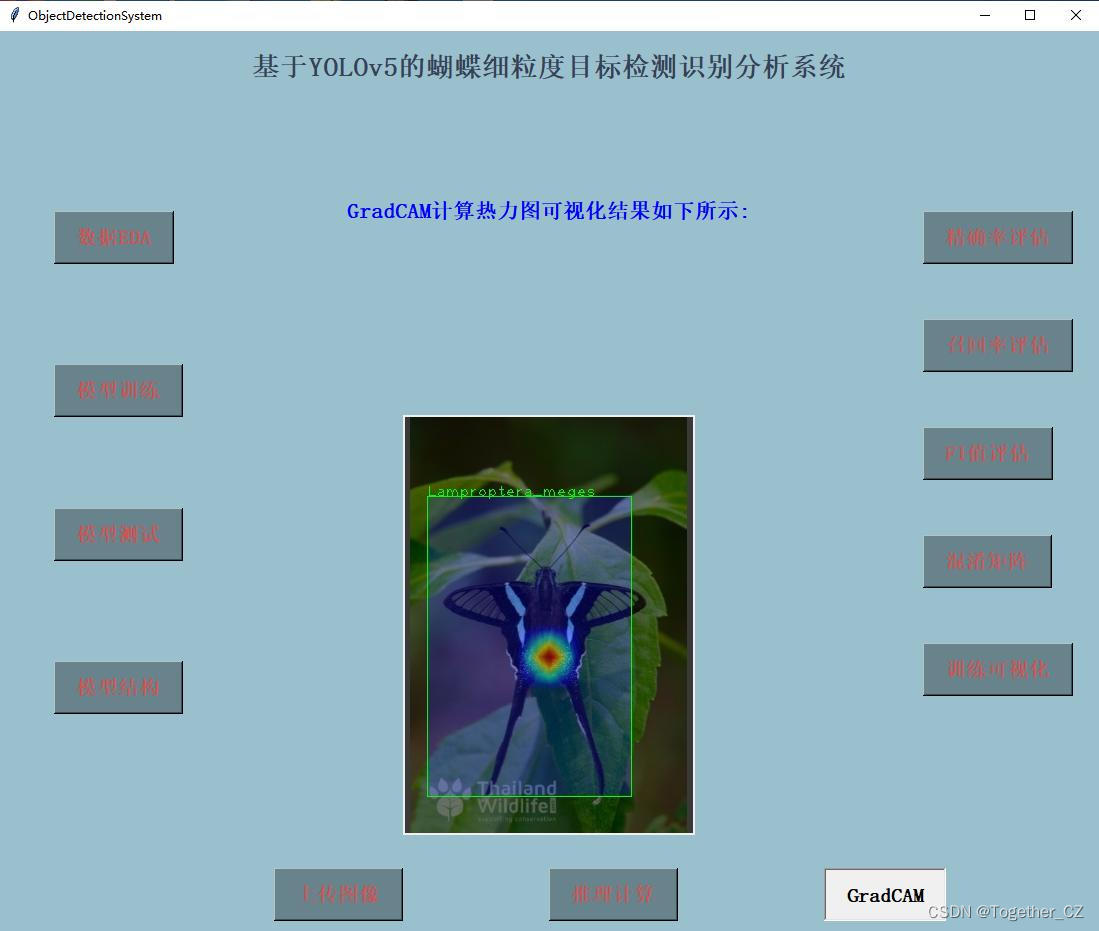
为了进一步分析计算模型检测识别的原理,这里集成了GradCAM进行热力图计算与可视化,实例效果如下所示:
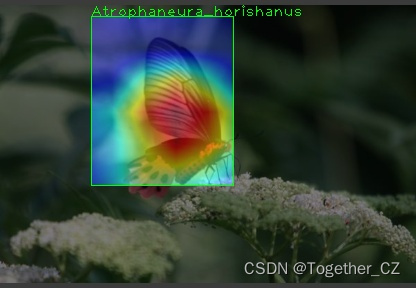

GradCAM核心代码实现如下所示:
import time
import torch
import torch.nn.functional as F
def find_yolo_layer(model, layer_name):
"""Find yolov5 layer to calculate GradCAM and GradCAM++
Args:
model: yolov5 model.
layer_name (str): the name of layer with its hierarchical information.
Return:
target_layer: found layer
"""
hierarchy = layer_name.split('_')
target_layer = model.model._modules[hierarchy[0]]
for h in hierarchy[1:]:
target_layer = target_layer._modules[h]
return target_layer
class YOLOV5GradCAM:
def __init__(self, model, layer_name, img_size=(640, 640)):
self.model = model
self.gradients = dict()
self.activations = dict()
def backward_hook(module, grad_input, grad_output):
self.gradients['value'] = grad_output[0]
return None
def forward_hook(module, input, output):
self.activations['value'] = output
return None
target_layer = find_yolo_layer(self.model, layer_name)
target_layer.register_forward_hook(forward_hook)
target_layer.register_backward_hook(backward_hook)
device = 'cuda' if next(self.model.model.parameters()).is_cuda else 'cpu'
self.model(torch.zeros(1, 3, *img_size, device=device))
print('[INFO] saliency_map size :', self.activations['value'].shape[2:])
def forward(self, input_img, class_idx=True):
"""
Args:
input_img: input image with shape of (1, 3, H, W)
Return:
mask: saliency map of the same spatial dimension with input
logit: model output
preds: The object predictions
"""
saliency_maps = []
b, c, h, w = input_img.size()
tic = time.time()
preds, logits = self.model(input_img)
print("[INFO] model-forward took: ", round(time.time() - tic, 4), 'seconds')
for logit, cls, cls_name in zip(logits[0], preds[1][0], preds[2][0]):
if class_idx:
score = logit[cls]
else:
score = logit.max()
self.model.zero_grad()
tic = time.time()
score.backward(retain_graph=True)
print(f"[INFO] {cls_name}, model-backward took: ", round(time.time() - tic, 4), 'seconds')
gradients = self.gradients['value']
print("gradients_shape: ", gradients.shape)
activations = self.activations['value']
print("activations_shape: ", activations.shape)
b, k, u, v = gradients.size()
k = 512
alpha = gradients.view(b, k, -1).mean(2)
print("alpha_shape: ", alpha.shape)
weights = alpha.view(b, k, 1, 1)
print("weights_shape: ", weights.shape)
print("activations_shape: ", activations.shape)
a,b,c,d=activations.shape
#activations = torch.reshape(activations, (1,32,c*4,d*4))
print("activations_shape: ", activations.shape)
saliency_map = (weights * activations).sum(1, keepdim=True)
saliency_map = F.relu(saliency_map)
saliency_map = F.upsample(saliency_map, size=(h, w), mode='bilinear', align_corners=False)
saliency_map_min, saliency_map_max = saliency_map.min(), saliency_map.max()
saliency_map = (saliency_map - saliency_map_min).div(saliency_map_max - saliency_map_min).data
saliency_maps.append(saliency_map)
return saliency_maps, logits, preds
def __call__(self, input_img):
return self.forward(input_img)
可视化界面实例推理如下所示: