💖作者：小树苗渴望变成参天大树
🎉作者宣言：认真写好每一篇博客
🎊作者gitee:gitee

如 果 你 喜 欢 作 者 的 文 章 ，就 给 作 者 点 点 关 注 吧！

---

前言

今天我们开始讲解动态规划的第二个题目，和第一个题目类似，但是按照动态规划的步骤却是不同的理解方式，所以我们来看看这个第二题是什么样的吧

---

第二题是三步问题

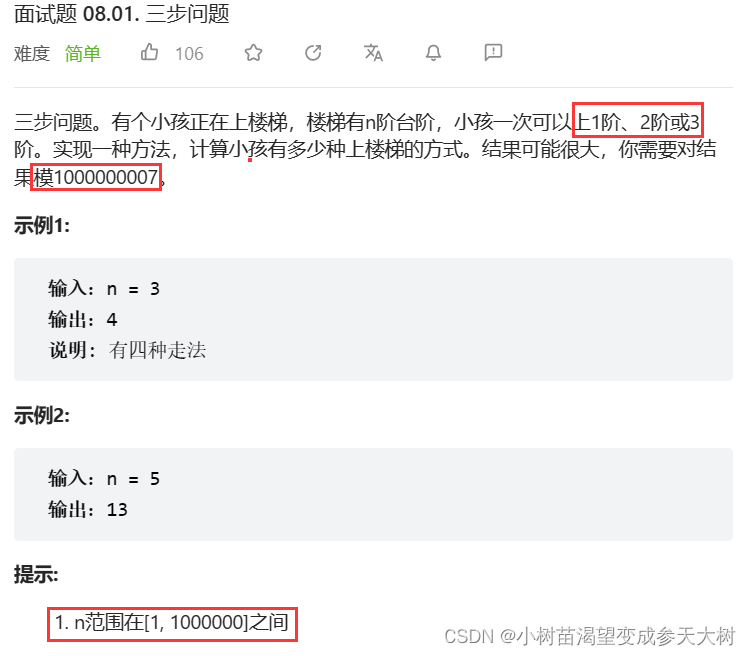
**题目解析：**看图解

通过图解，我们知道了怎么解决这个题目，我们开始走 动态规划的五个步骤：

1. 状态表示
   就是dp[i]表示，当台阶数到达i位置的时候，小孩有几种上台阶的方式

2. 状态转移方程
   以i位置的状态，找离此状态最近的状态和此状态的关系
   
   因为只有走一阶，二阶，三阶，所以离此状态最近也就是三种状态，随意状态转移方程为：dp[i]=dp[i-1]+dp[i-2]+dp[i-3]

3. 初始化
   保证数组不越界，和第一题一样，不能出现负数下标，所以献给前三个dp表数据初始化 dp[1]=1 dp[2]=2 dp[3]=4

4. 填表顺序
   从左往右按照顺序进行填写

5. 返回值
   根据条目要求，dp[i]就是对应多少种，所以第n个台阶的状态就是返回值为dp[n]

代码实现：

class Solution {
public:
    int waysToStep(int n) {
        const int MOD=1000000007;
        //越界处理
        if(n==1)return 1;
        if(n==2)return 2;
        if(n==3)return 4;
    //1.创建dp表
     int*dp =new int[n+1];
    //2.初始化
    dp[1]=1; dp[2]=2; dp[3]=4;
    //3.根据状态转移方程些代码
    for(int i=4;i<=n;i++)
    {
        dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;//这个相加之后可能超出int的范围
    }
    //4.返回值
    return dp[n];
    }
};

按照此题也可以用滚动数组来进行空间优化，因为和钱买你一样的，我就不做介绍，大家可以自己下来去实现一下
运行结果：

到这里我就讲解完动态规划的第二道题目，希望大家下来好好理解一下，我们下道题目再见