稀疏向量通常包含许多维度，而创建 特征交叉 则会产生更多维度。考虑到如此高维的特征向量，模型可能会变得巨大且需要大量的 RAM 资源。

在高维稀疏向量中，最好将权重精确地下降到 0。权重恰好为 0 本质上意味着从模型中删除相应的特征，即该特征不再作为模型的输入。此外，将特征归零可节省 RAM，并减少模型中的噪声。

例如，考虑一个不仅涵盖加利福尼亚州而且涵盖整个全球的住房数据集。以分（角分）级别（每度 60 分）存储全球纬度，在稀疏编码中提供大约 10,000 个维度；分级别的全球经度给出了大约 20,000 个维度。这两个特征的特征交叉将产生大约 200,000,000 个维度。这 200,000,000 个维度中的许多维度代表的居住区域非常有限（例如海洋中的位置），因此很难使用这些数据进行有效概括。存储这些不需要的维度，不仅 RAM 成本高昂，而且是愚蠢的。因此，最好将无意义维度的权重恰好降至 0，这样我们就可以避免在推理时支付这些模型系数的存储成本。

通过添加适当选择的正则化项，我们也许能够将这个想法编码到训练时完成的优化问题中。那么，在【机器学习10】中介绍的 L2 正则化能完成这项任务吗？显然是不能的。L2 正则化鼓励权重变小，但不会强制它们恰好为 0.0。

另一种想法是尝试创建一个正则化项来惩罚模型中非零系数值的计数。仅当模型拟合数据的能力有足够的增益时，增加此计数才是合理的。不幸的是，虽然这种基于计数的方法直观上很有吸引力，但它会将我们的凸优化问题变成非凸优化问题。所以这个被称为 L0 正则化的想法并不是我们可以在实践中有效使用的。

然而，有一个称为 L1 正则化的正则项，作为 L0 的近似值，它具有凸性的优点，因此计算效率高。因此，我们可以使用 L1 正则化来将模型中的那些无信息系数恰好降低为 0，从而在推理时节省 RAM。

2.L1 与 L2 正则化。

L2 和 L1 对权重的惩罚不同：

• L2 惩罚 。
• L1 惩罚 。

因此，L2 和 L1 具有不同的导数：

• L2 的导数是 2 *权重。
• L1 的导数是 k（常数，其值与权重无关）。

为了便于理解，我们可以将 L2 的导数视为每次移除 “x%*权重” 的力。根据  Zeno  理论，即使你删除某个数字的百分之 x 数十亿次，减少的数字永远不会完全达到零（如“割圆术”所言，每次减少1/2，万世不竭）。无论如何，L2 通常不会将权重降低到零。

同样的，可以将 L1 的导数视为每次从重量中减去某个常数的力。然而，由于绝对值的原因，L1 在 0 处具有不连续性，这导致与 0 交叉的减法结果被清零。例如，如果减法将权重从 +0.1 强制到 -0.2，则 L1 会将权重设置为恰好 0。显然，L1 可将权重归零。

L1 正则化（惩罚所有权重的绝对值）对于宽模型来说非常有效。需要注意的是，此描述对于一维模型来说是正确的。

相同情况下，相较于 L2 正则化，L1 正则化具有以下特点：

• 从 L2 正则化切换到 L1 正则化会极大地减少测试损失和训练损失之间的增量
• 从 L2 正则化切换到 L1 正则化会抑制所有学习到的权重
• 增加 L1 正则化率通常会抑制学习权重；然而，如果正则化率太高，模型无法收敛并且损失非常高。

3.L1 正则化的数学内涵

L1 正则化的策略是在原始的目标函数后面加上一个 L1 范数，也就是惩罚项为：

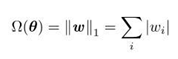
添加惩罚项后的正则化目标函数数学形式为：

对应的梯度为：

其中 sign(w) 只是简单地取 w 各个元素的正负号：

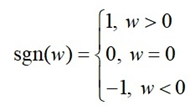
则权重的更新公式为：

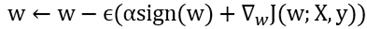
展开后公式为：

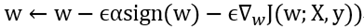
从权重更新公式可以看出，因为 sign(w) 的存在，当 w>0 时，梯度下降时更新后的 w 变小，当w<0 时，梯度下降时更新后的 w 变大，换言之，L1 正则化使得权重 w 往 0 靠，使网络中的权重尽可能为 0，也就相当于减小了网络复杂度，防止过拟合。

这也是 L1 正则化会产生更稀疏的解的原因。此处稀疏性指的是最优值中的一些参数为 0。特征稀疏的好处有以下两点：

• 特征选择。现实世界中，问题的特征的数量往往是很大的，而起决定性作用的往往是一小部分，稀疏规则化算子的引入会学习去掉这些没有信息的特征，也就是把这些特征对应的权重置为 0。
• 可解释性。例如对于某种疾病的预测问题，可能有上千个特征，如果主要特征只有 5 个，那么我们有理由相信，患不患病只和这 5 个特征有关，其它特征暂不考虑也不会有太大影响。

4.参考文献

1-深度学习基础算法系列（3）-正则化之L1/L2正则化 - 知乎

2-稀疏性正则化：L1 正则化  |  Machine Learning  |  Google for Developers