题目来源：https://leetcode.cn/problems/trim-a-binary-search-tree/description/

 

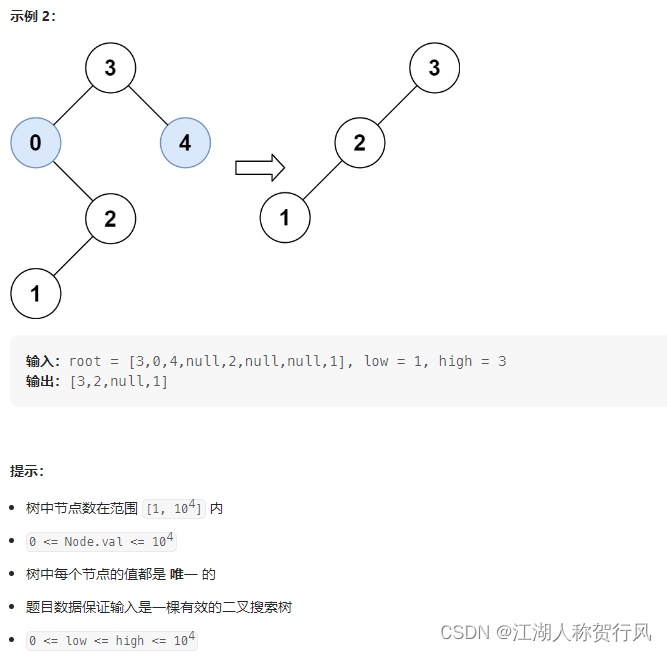
 C++题解1：递归法。当前节点为空时返回空，不为空时对其值进行分类讨论。以low为例，当前节点值等于low时，意味着其左子树都要丢弃，可指向空；大于low时，说明其左子树也可能满足条件，因此对其左子树进一步递归；小于low时，说明当前节点及其左子树都不满足条件，将当前节点更新为其右子节点。

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(!root) return nullptr;
        if(root->val == low) root->left = nullptr; 
        else if(root->val > low) {
            root->left = trimBST(root->left, low, high);
        }
        else {
            root = root->right;
            return trimBST(root, low, high);
        }
        if(root->val == high) root->right = nullptr;
        else if(root->val < high) {
            root->right = trimBST(root->right, low, high);
        }
        else {
            root = root->left;
            return trimBST(root, low, high);
        }
        return root;
    }
};

C++题解2：递归法。大致思路同上，较为精简，来源代码随想录。

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == nullptr) return nullptr;
        if (root->val < low) return trimBST(root->right, low, high);
        if (root->val > high) return trimBST(root->left, low, high);
        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        return root;
    }
};

C++题解3：迭代法。见注释，来源代码随想录。

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int L, int R) {
        if (!root) return nullptr;

        // 处理头结点，让root移动到[L, R] 范围内，注意是左闭右闭
        while (root != nullptr && (root->val < L || root->val > R)) {
            if (root->val < L) root = root->right; // 小于L往右走
            else root = root->left; // 大于R往左走
        }
        TreeNode *cur = root;
        // 此时root已经在[L, R] 范围内，处理左孩子元素小于L的情况
        while (cur != nullptr) {
            while (cur->left && cur->left->val < L) {
                cur->left = cur->left->right;
            }
            cur = cur->left;
        }
        cur = root;

        // 此时root已经在[L, R] 范围内，处理右孩子大于R的情况
        while (cur != nullptr) {
            while (cur->right && cur->right->val > R) {
                cur->right = cur->right->left;
            }
            cur = cur->right;
        }
        return root;
    }
};