2023年华中杯数学建模
C题 空气质量预测与预警
原题再现
空气污染对人类健康、生态环境、社会经济造成危害,其污染水平受诸多因素的影响,如 PM2.5、PM10、CO、气温、风速、降水量等,探究 PM2.5 等污染物浓度的因素,更精准的预测 PM2.5 浓度和 AQI 指数等是科学界和决策者共同关心的问题,对于解析污染影响因素和有效制订控制策略具有重要意义。
为了健全和针对完善重污染天气的应对处置机制,提高重污染天气预防预警、应急响应能力和环境精细化管理水平,消除重度及以上污染天气,作为突发环境事件应急预案体系的重要组成部分,某地发布污染天气应急预案,该预案将加强监测预警和节能减排,最大程度降低污染天气的影响。其预警等级划分为四级应急响应:
蓝色预警:预测日 AQI>150 或日 AQI>100 持续 48 小时及以上。
黄色预警:预测日 AQI>200 或日 AQI>150 持续 48 小时及以上。
橙色预警:预测日 AQI>200 持续 48 小时或日 AQI>150 持续 72 小时及以上。
红色预警:预测日 AQI>200 持续 72 小时且日 AQI>300 持续 24 小时及以上。
请参赛团队根据问题要求,完成以下问题(任务):
问题一:根据附件 1 和附件 2,对数据进行分析和处理,筛选出与 PM2.5 浓度变化有关的因素,并说明筛选出的因素对 PM2.5 浓度影响的程度。
问题二:自行划分训练集和测试集,根据附件 1 和附件 2,基于问题一构建 PM2.5 浓度多步预测模型,分别使用均方根误差(RMSE)对 3 步、5 步、7 步、12 步预测效果进行评估,其结果请用表 1 格式在正文中具体给出,并对测试集及其预测结果进行可视化。同时,用该模型预测附件 3 所给定时间的 PM2.5 浓度,其结果请用表 2 格式在正文中具体给出。


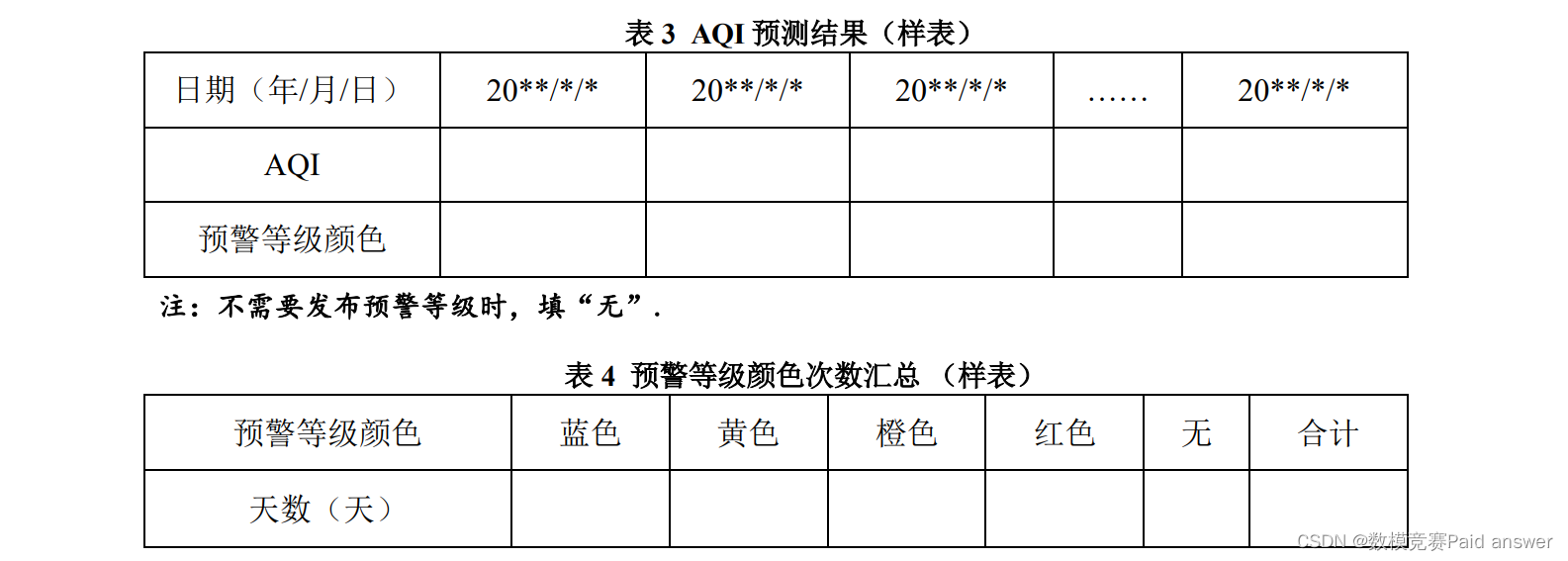
问题三:构建 AQI 多步预测模型,使用均方根误差(RMSE)对建模效果进行评估,并对测试集及其预测结果进行可视化。同时,用该模型预测附件 3 所给定时间的 AQI,并给出每天空气质量的预警等级,其结果请用表 3 和表 4 格式在正文中具体给出。
附件说明:
1. 附件 1 和附件 2 提供了该监测点近年来空气质量预报基础数据,包括污染物浓度数据(见附件 1)和气象数据(见附件 2)。
2. 附件 3 为待预测时间点。
整体求解过程概述(摘要)
空气污染是人类目前所面临的最严峻问题之一,其可对人体健康、生态环境等方面造成严重损害。伴随着城市化与工业化的不断深入,我国目前的污染现状愈发严重。故精确有效地对空气质量指标数据进行预测以及对未来空气状态作出预警,对生态健康、社会发展等均具有深远意义。
针对问题一,为分析得到与 PM2.5 浓度变化相关的指标因素及其对该浓度变化的影响程度,欲对所给数据进行预处理。首先对附件 1 中所给数据特点进行分析,利用多重插补对空缺值进行补全处理。再剔除附件 2 中的异常值,利用 Lagrange 插补法对其缺失值进行填充。将处理后的数据进行整合,其后,为克服数据间量纲差异过大的影响,对插补所得数据进行标准化处理。再对标准化后数据采用正态性检验,结合显著性水平与 Q-Q 图统计描述,可分析发现大部分指标数据未呈现正态分布,未在Pearson 相关系数适用范围之内,故选用 Spearman 相关系数对各指标间的相关性进行计算和分析。最终提取出与 PM2.5 浓度较强相关的五个变量分别为 SO2、NO2、CO、PM10 和平均气温,再对其进行显著性检验,其结果表明 PM10 与其呈现极强相关,NO2、CO 与其呈现强相关,SO2、平均气温与其呈现中等程度相关。
针对问题二,为预测所给定时间段的 PM2.5 浓度,结合其历史数据的散点图特点,首先建立 ARIMA 预测模型对其进行预测,得到未来 12 天的各空气质量指标相对应的预测数据,并对其预测效果进行评价,分析得出其预测效果不佳。综合考虑后选用LSTM 多步预测模型再对其进行预测。提取出问题一中相关性分析筛选出的五个指标作为 LSTM 模型中的输入因子,将 PM2.5 浓度设置为输出变量。将选取的指标数据导入 Python 并进行标准化处理,为防止过度拟合,选用前 80%的数据为训练集,后20%为测试集。通过设置 LSTM 层数、神经元数量、优化器等,建立得出 LSTM 神经网络预测模型,并对测试集及其预测结果进行可视化处理。其后,通过改变预测步长,得出 3 步、5 步、7 步和 12 步预测结果的均方根误差(RMSE),其值分别为 19.4574 、21.6210、21.4685 和 22.0202。将两模型进行对比分析,最终选用拟合度更优、预测精确度更高的 LSTM 多步预测模型对未来 12 天 PM2.5 浓度进行预测,所得出的预测数据见表 6-3。对 LSTM 多步预测模型的 MAE、R2、MAPE、残差与损失曲线进行分析,得出模型具有一定的准确性与稳健性。
针对问题三,为构建 AQI 多步预测模型,首先计算分析出 AQI 与其余各项检测指标间的 Spearman 相关系数,筛选得出 PM10、SO2、PM2.5、NO2和 CO 为其主要影响因子。其后分别运用 ARIMA 模型与 LSTM 模型对未来 12 天空气质量的的 AQI 指数进行预测,自主划分训练集与预测集并将预测结果可视化,其中,LSTM 模型的均方根误差(RMSE)为 32.2989,综合评估分析得出其预测效果较好。进而,基于所得到的未来 12 天的 AQI 指数大小,分析得出其相对应的空气质量等级及预警等级,并将预警等级颜色次数进行汇总处理,上述具体结果分别见表 7-2 和表 7-3。
模型假设:
1. 假设空气污染仅与所给检测指标相关,不考虑其他因素影响。
2. 假设所给数据除缺失值和异常值外均真实可靠且具有强代表性。
3. 假设缺失值和异常值处理后的数据是平滑的,可满足后续模型计算需求。
问题分析:
问题一的分析
针对附件中所给数据,发现其中部分指标所对应数据存在缺失值与异常值,结合各表所给数据的数据特点,考虑对附件 1 中缺失机制为 MAR 且出现连续缺失现象的空缺值采用多重插补法进行填充,故利用其对附件 1 中缺失值与部分指标中出现的异常值 0 值进行插补处理。而针对附件 2 中出现的样本较少的异常值,进行剔除处理后选用计算量较小的拉格朗日差值法进行填充补全。进而再对插补后数据进行标准化处理,并采用正态性检验。根据检验出的各空气质量检测指标结果,结合 Q-Q 图对其统计描述,判断出大部分所给数据不服从正态分布,与皮尔逊相关系数适用范围相违,故选用斯皮尔曼相关系数对其进行相关性分析和显著性检验。根据所得结果,筛选出与 PM2.5 浓度变化相关的因素,并分析其对 PM2.5 浓度变化的影响程度。其分析流程图如图 2-1 所示。
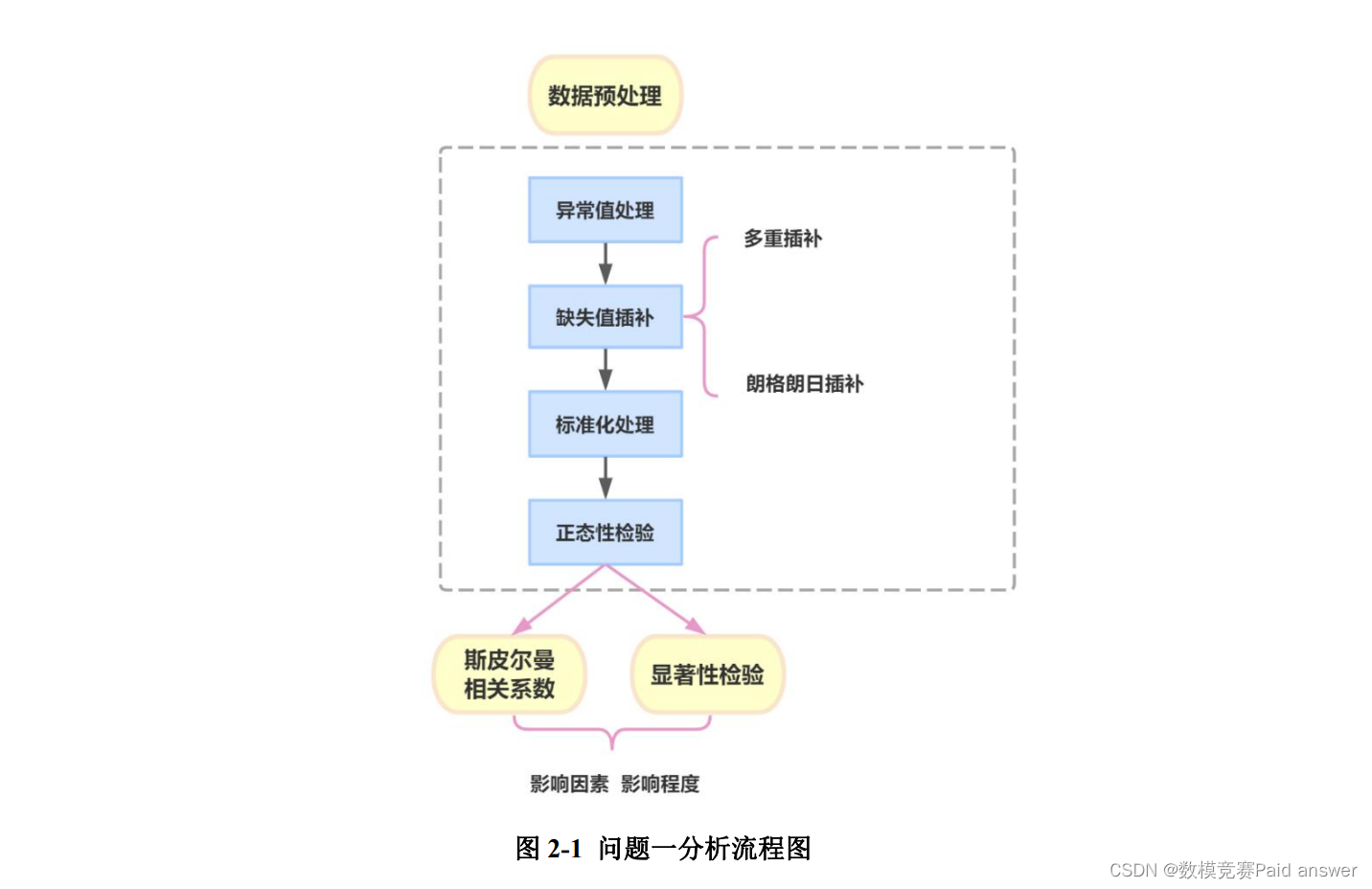
问题二的分析
为更好预测 PM2.5 的浓度,同时采用 ARIMA 模型与 LSTM 模型对其进行预测,并将预测结果相对比后得出最优预测模型。针对 ARIMA 模型,首先对 PM2.5 浓度序列进行平稳性检验,并通过差分处理将其转化为可使用与 ARIMA 模型的平稳序列。再对该序列进行残差白噪声检验分析,使数据满足模型拟合要求。最后对通过检测的数据选择合适的 ARIMA 模型进行拟合处理,并得出相关预测结果。基于 LSTM 神经网络模型对时间序列较好的预测效果,选择输入影响因子、输出变量、神经元数量,设置合理的超参数等来建立 LSTM 多步预测模型。通过改变预测步长来得到 3、5、7与 12 步预测模型的均方根误差(RMSE),并以已建立好的神经网络模型与已知的历史数据来预测未来 12 天的 PM2.5 浓度大小。
问题三的分析
考虑到问题二所建立的 LSTM 多步预测模型对数据的预测效果较好,用该模型来预测未来 12 天 AQI 的数据。首先利用 Spearman 相关系数分析得到影响 AQI 大小的五个相对重要指标,并与 AQI 的计算方式相结合,建立多输入、单输出的 LSTM 多步预测模型,通过计算模型的均方根误差(RMSE)来评估建模效果。同样,通过建立 ARIMA 预测模型来进行对比。综合考虑后得出未来 12 天 AQI 的数据大小、每天空气质量的预警等级以及预警等级颜色的汇总。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
%lagrange insert
function y=lagranges(x0,y0,x)
n=length(x0);m=length(x);
for i=1:m
z=x(i);
s=0.0;
for k=1:n
p=1.0;
for j=1:n
if j~=k
p=p*(z-x0(j))/(x0(k)-x0(j));
end
end
s=p*y0(k)+s;
end
y(i)=s;
end
%lagrange insert
function y=lagranges(x0,y0,x)
n=length(x0);m=length(x);
for i=1:m
z=x(i);
s=0.0;
for k=1:n
p=1.0;
for j=1:n
if j~=k
p=p*(z-x0(j))/(x0(k)-x0(j));
end
end
s=p*y0(k)+s;
end
y(i)=s;
end
end
end
LOGL = reshape(LOGL,16,1);
PQ = reshape(PQ,16,1);
[~,bic] = aicbic(LOGL,PQ+1,100);
a=reshape(bic,4,4)
%reshape 重构数组
a_max=max(a(:));
[x,y]=find(a==min(a(:)));
%找最佳 lags 值
Mdl = arima(x, 1, y); %第二个变量值为 1,即一阶差分
EstMdl = estimate(Mdl,Y);
[res,~,logL] = infer(EstMdl,Y); %res 即残差
stdr = res/sqrt(EstMdl.Variance);
figure('Name','残差检验')
subplot(2,3,1)
plot(stdr)
title('Standardized Residuals')
subplot(2,3,2)
histogram(stdr,10)
title('Standardized Residuals')
subplot(2,3,3)
autocorr(stdr)
subplot(2,3,4)
parcorr(stdr)
subplot(2,3,5)
qqplot(stdr)
%上图为残差检验的结果图。
% Standardized Residuals 是查看残差是否接近正态分布
% ACF 和 PACF 检验残差的自相关和偏自相关
% 最后一张 QQ 图是检验残差是否接近正太分布的
% Durbin-Watson 统计是计量经济学分析中最常用的自相关度量
diffRes0 = diff(res);
SSE0 = res'*res;
DW0 = (diffRes0'*diffRes0)/SSE0 % Durbin-Watson statistic,
step = 12; %预测步数为 12
[forData,YMSE] = forecast(EstMdl,step,'Y0',Y);
lower = forData - 1.96*sqrt(YMSE); %95 置信区间下限
upper = forData + 1.96*sqrt(YMSE); %95 置信区间上限
figure()
plot(Y,'Color',[.7,.7,.7]);
hold on
h1 = plot(length(Y):length(Y)+step,[Y(end);lower],'r:','LineWidth',2);
plot(length(Y):length(Y)+step,[Y(end);upper],'r:','LineWidth',2)
h2 = plot(length(Y):length(Y)+step,[Y(end);forData],'k','LineWidth',2);
legend([h1 h2],'95% 置信区间','预测值',...
'Location','NorthWest')
title('Forecast')
X=3030:1:3041;
plot(X,test,'color',[0.5 0.5 0.5])
hold off