作者在前面的两篇文章中介绍了标准粒子群及其变体,**由于PSO算法需要设定的参数(惯性因子w,学习因子 c1,c2)太多,不利于找到待优化模型的最优参数,而且粒子位置变化缺少随机性,容易陷入局部最优。**针对这些问题,本文提出一种性能更高的优化算法—量子粒子群优化算法(Quantum Particle Swarm Optimization,QPSO),下面将详细介绍其理论与实现。
00 文章目录
1 量子粒子群优化算法
2 代码目录
3 问题导入
4 仿真
5 源码获取
01 量子粒子群优化算法
量子粒子群优化算法取消了粒子的移动方向属性,相比较于粒子群算法,粒子位置的更新跟该粒子之前的运动没有任何关系,是量子编码与量子门计算进行更新,这样就增加了粒子位置的随机性,避免发生局部过早收敛。
1.1 量子粒子群优化算法原理
量子粒子群算法控制参数少,只有一个,且收敛度快,具有良好的性能。对于标准粒子群算法,粒子的位置和速度共同决定了粒子的运动轨迹,在牛顿力学中粒子沿着确定的轨迹运动。在量子力学中,轨迹项是没有意义的,因为粒子的位置和速度根据测不准原理无法同时确定。因此 QPSO 中粒子的运动行为与 PSO大相径庭。在量子粒子群算法中,粒子是由薛定谔方程描述 ψ( x, t),而不是标准粒子群算法的位置和速度。为保证算法的收敛需满足下式,每一粒子要收敛于各自的 p 点,对任意粒子i有p (pi1 , pi2 ,…, pid ),pid 是第i个粒子在第d维的值,其中φij(t)为0和1之间的随机函数。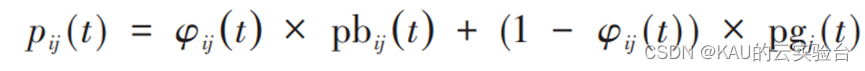
QPSO 算法引入的新名词 mb来达到优化粒子群全局最优的搜索过程,mb表示pbest的平均值,即平均粒子历史最优位置,公式为:
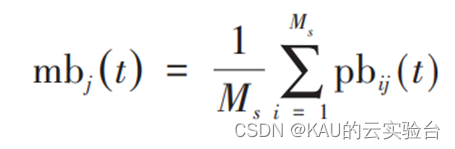
其中,Ms是粒子群的个数;j 为粒子的第 j 维其取值范围为j∈[1,d]。可得全局极值的平均值 La 的计算公式为: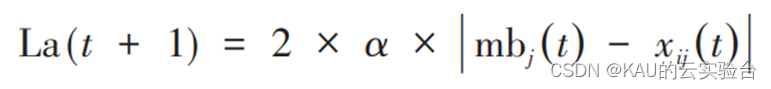
进而可得到粒子的进化方程为: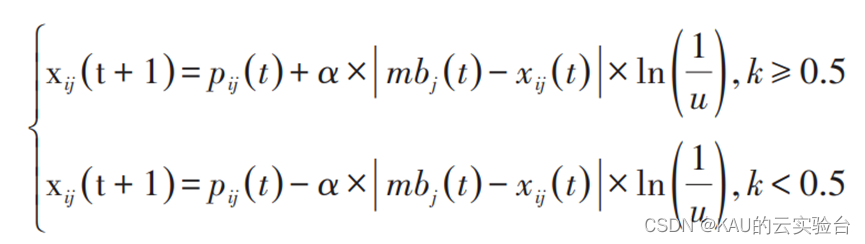
u和k是在[0,1]范围产生的均匀随机数,其中 α 是收缩-扩张因子,是量子粒子群唯一的参数,调节它的值能控制算法的收敛速度,但由于当α 固定时,算法对粒子群规模和最大迭代次数都是敏感的,如果采用时变的α,则算法性能将获得提高,故对于收缩-扩张因子的选择对于性能是有影响的。综上可以看出,量子粒子群算法具有调节参数少、收敛速度快的优点。
1.2 收缩-扩张因子
若采用固定的收缩-扩张因子,则算法的鲁棒性会降低. 通常采用自适应变化的收缩-扩张因子,可以 在迭代后期改善算法局部搜索的精度,本文选取线性递减策略自适应的修改收缩-扩张因子:
其中: Kmax为最大迭代次数; α0, α1为预设值,一般取 α0 = 0.5, α1 = 1。
当然,收缩-扩张因子还有许多可选变式,这篇作为量子粒子群的引入文章先介绍其中一种,后续会介绍其它变式。
收缩-扩张因子随着迭代次数的变化关系如图: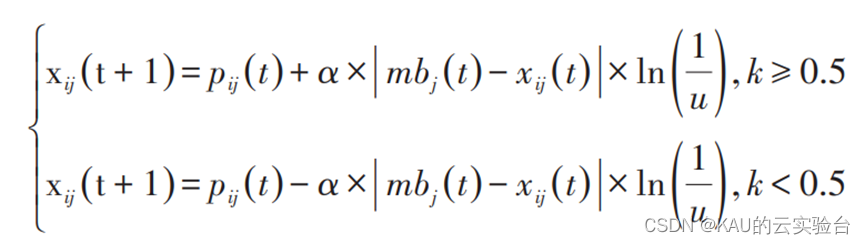
02 代码目录
首先运行main_pso.m与main_qpso.m,再运行compare.m即可看到迭代对比
03 问题导入
为验证算法的性能,采用Benchmark中的1个常用的测试函数Rastrigrin函数: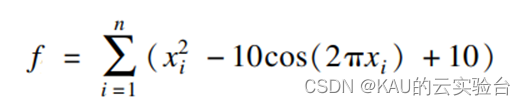
‘
将该函数取负,则适应度为越大越佳。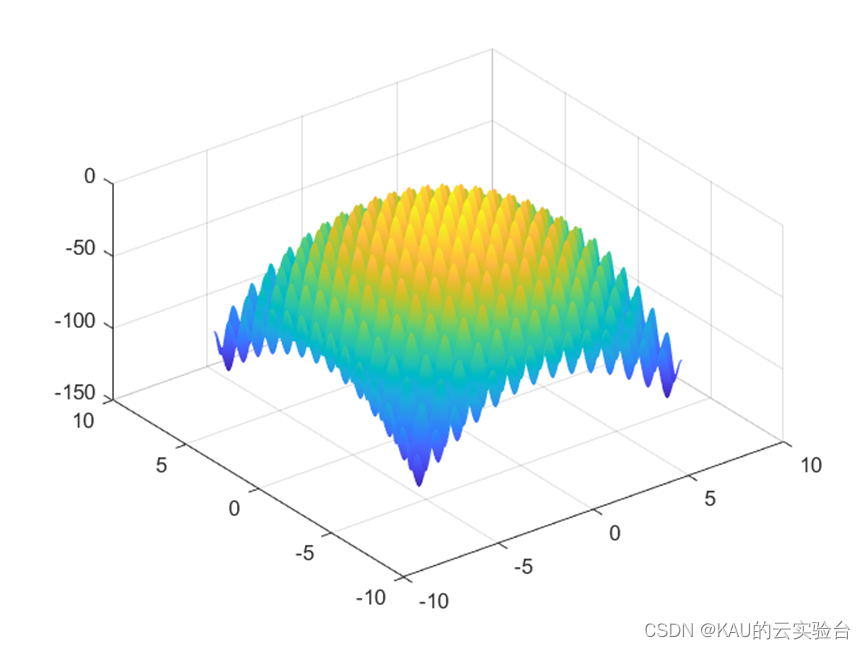
该函数为多峰函数,收敛于(0,0,…,0)。
04 仿真
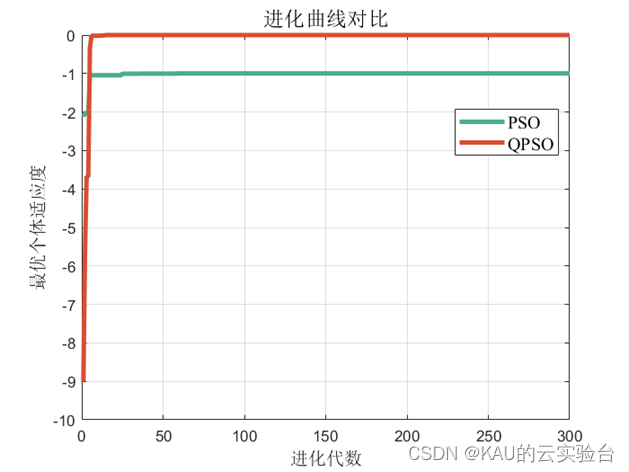
将量子粒子群与标准粒子群通过Rastrigrin函数进行对比,得到如下结果: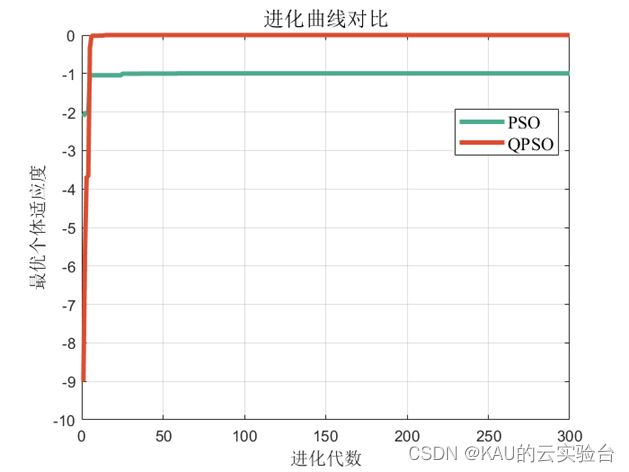
显然,量子粒子群的收敛速度和全局寻优能力都强于标准粒子群,而标准粒子群则陷入了局部最优解。
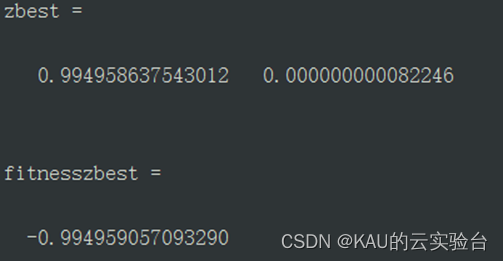
其中,QPSO的取值以及适应度为
:
PSO的取值以及适应度为:
05 源码获取
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 源码 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
https://mbd.pub/o/bread/ZJqclpxr
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 源码 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
部分源码:
%% 量子粒子群算法应用于函数寻优,适应度为越大越好
% QPSO算法取消了粒子的移动方向属性 即惯性因子w 学习因子c1,c2
%% 粒子群参数
popsize = 20;% 群体规模
MAXITER = 300;% 最大迭代次数
dimension = 2;%问题维数
irange_l = [-2,-2];%位置初始化下界
irange_r = [2,2];%位置初始化上界
xmax = 0.5;% 搜索范围上界
xmin = -0.5;%搜索范围下界
M = (xmax - xmin)/2;%搜索范围的中值
sum1 = 0;
st = 0;
runno= 1;%算法运行x轮
yy2 = zeros( runno,MAXITER);%记录每一轮中每一迭代步的最好适应值
%% 初始化
T= cputime;%记录CPU时间
x = ( irange_r- irange_l) .* rand( popsize,dimension,1) + irange_l; %初始化粒子当前位置
pbest = x;%将粒子个体最好位置初始化为当前最好位置
gbest = zeros( 1,dimension) ;%初始化全局最好位置变量
for i= 1 : popsize%计算当前位置和个体最好位置的适应值
f_x(i) = RA(x(i, : ));
f_pbest(i)= f_x(i);
end
如果这篇文章对你有帮助或启发,可以点击右下角的赞 (ง •̀_•́)ง(不点也行),若有定制需求,可私信作者。