✅作者简介：人工智能专业本科在读，喜欢计算机与编程，写博客记录自己的学习历程。
🍎个人主页：小嗷犬的个人主页
🍊个人网站：小嗷犬的技术小站
🥭个人信条：为天地立心，为生民立命，为往圣继绝学，为万世开太平。

---

---

层次分析法

层次分析法，简称 AHP，是指将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。该方法是美国运筹学家匹茨堡大学教授萨蒂于 20 世纪 70 年代初，在为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时，应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。

层次分析法一般包括以下几个步骤：

1. 建立层次结构模型
2. 构造判断矩阵
3. 层次单排序及其一致性检验
4. 层次总排序及其一致性检验

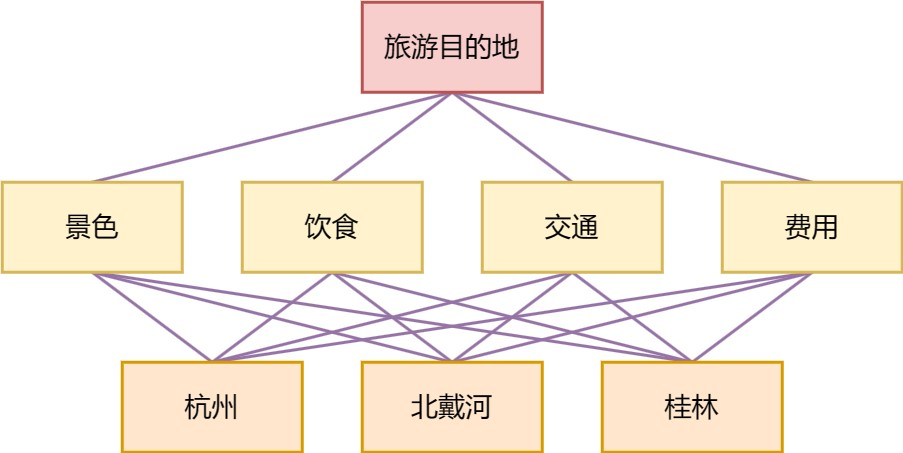
建立层次结构模型

将将决策的目标、考虑的因素(决策准则)和决策方案，按它们之间的相互关系分为最高层、中间层和最低层，画出层次结构图。

• 最高层：目标层。决策的目的、要解决的问题。
• 中间层：准则层。考虑的因素、决策的准则。
• 最低层：方案层。决策时可供选择的方案。

构造判断矩阵

在确定各层次各因素之间的权重时，如果只是定性的结果，则常常不容易被别人接受，因而 Saaty 等人提出一致矩阵法，即不把所有因素放在一起比较，而是两两相互比较，对此时采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。如对某一准则，对其下的各方案进行两两对比，并按其重要性程度评定等级。$a_{ij}$ 为要素 $i$ 与要素 $j$ 重要性比较结果，按两两比较结果构成的矩阵称作判断矩阵，判断矩阵具有如下性质：

$$a_{ij}>0,a_{ij}=\frac{1}{a_{ji}},a_{ii}=1$$

下表列出了 Saaty 给出的 9 个重要性等级及其赋值：

因素 $i$ 与因素 $j$ 的重要性比较结果	量化值
$i$ 与 $j$ 同等重要	1
$i$ 比 $j$ 稍微重要	3
$i$ 比 $j$ 较强重要	5
$i$ 比 $j$ 强烈重要	7
$i$ 比 $j$ 极端重要	9
两相邻判断的中间值	2, 4, 6, 8

层次单排序及其一致性检验

对应于判断矩阵最大特征根 ${\lambda }_{max}$ 的特征向量，经归一化（使向量中各元素之和等于 1）后记为 $W$。$W$ 的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值，这一过程称为层次单排序。得到的 $W$ 称为单层权向量。

计算得到的单层权向量 $W$ 是否合理，取决于判断矩阵是否一致，一个完全一致的判断矩阵 $A$ 应满足以下条件：

a i j a j k = a i k , ∀ i , j , k ∈ { 1 , 2 , ⋯   , n } a_{ij}a_{jk} = a_{ik}, \forall i, j, k \in \{1, 2, \cdots, n\} aij​ajk​=aik​,∀i,j,k∈{1,2,⋯,n}

但事实上，由于人们的主观性，构造出来的判断矩阵很难做到完全一致，因此人们引入了一致性指标 $CI$ 来衡量判断矩阵的一致性，$CI$ 的计算公式为：

$$CI=\frac{{\lambda }_{max}-n}{n-1}$$

• 当 $CI=0$ 时，判断矩阵 $A$ 完全一致。
• 当 $CI>0$ 时，判断矩阵 $A$ 不一致。
• 当 $CI$ 值越大，判断矩阵 $A$ 不一致程度越大。

为了衡量 $CI$ 的大小，引入了随机一致性指标 $RI$：

$$RI=\frac{1}{n}\sum _{i=1}^{n}C{I}_i$$

一般情况下，矩阵阶数越大，则出现一致性随机偏离的可能性也越大，即 $RI$ 的值会随着 $n$ 的增大而增大，$RI$ 的值与 $n$ 的关系如下表所示：

$n$	1	2	3	4	5	6	7	8	9	10
$RI$	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

考虑到一致性的偏离可能是由于随机原因造成的，因此在检验判断矩阵是否具有满意的一致性时，还需将 $CI$ 和随机一致性指标 $RI$ 进行比较，得出一致性比例 $CR$ ，公式如下：

$$CR=\frac{CI}{RI}$$

通常情况下，我们认为：

• 当 $CR<0.1$ 时，判断矩阵 $A$ 具有满意的一致性。
• 当 $CR>0.1$ 时，判断矩阵 $A$ 不具有满意的一致性。

层次总排序及其一致性检验

计算某一层次所有因素对于最高层(总目标)相对重要性的权值，称为层次总排序。这一过程是从最高层次到最低层次依次进行的。

对于第 $k$ 层次，设其一致性指标为 $C{I}_{(k)}$，随机一致性指标为 $R{I}_{(k)}$，则有：

$$\begin{gathered} C{I}_{(k)}=C{I}_{(k)}^T{W}_{(k-1)} \\ R{I}_{(k)}=R{I}_{(k)}^T{W}_{(k-1)} \end{gathered}$$

第 $k$ 层次的一致性比例为：

$$C{R}_{(k)}=\frac{C{I}_{(k)}}{R{I}_{(k)}}$$

评判标准与层次单排序相同。

---

层次分析法解志愿填报问题

问题描述

小李需要填报考研志愿，已经确定了 3 个方案，需要你从专业认可度、院校认可度、院校所在地、考研难易 4 个方面进行评估，最终确定最佳方案。

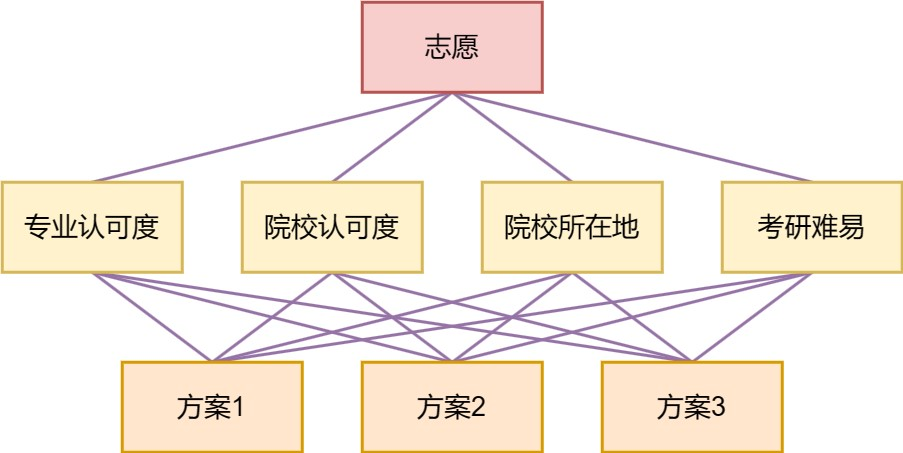
小李给出的准则层判断矩阵如下：

$$A=\left[\begin{array}{cccc}1& 2& 4& 2\\ 1/2& 1& 3& 2\\ 1/4& 1/3& 1& 1/3\\ 1/2& 1/2& 3& 1\end{array}\right]$$

小李对预选的 3 个方案进行了两两比较，得到的判断矩阵如下：

$$B_1=\left[\begin{array}{ccc}1& 4& 6\\ 1/4& 1& 2\\ 1/6& 1/2& 1\end{array}\right],B_2=\left[\begin{array}{ccc}1& 2& 3\\ 1/2& 1& 2\\ 1/3& 1/2& 1\end{array}\right],B_3=\left[\begin{array}{ccc}1& 8& 1\\ 1/8& 1& 1/9\\ 1& 9& 1\end{array}\right],B_4=\left[\begin{array}{ccc}1& 2& 4\\ 1/2& 1& 3\\ 1/4& 1/3& 1\end{array}\right]$$

MATLAB 求解

% 准则层判断矩阵
A = [1 2 4 2; 1/2 1 3 2; 1/4 1/3 1 1/3; 1/2 1/2 3 1];

% 方案层判断矩阵
B1 = [1 4 6; 1/4 1 2; 1/6 1/2 1];
B2 = [1 2 3; 1/2 1 2; 1/3 1/2 1];
B3 = [1 8 1; 1/8 1 1/9; 1 9 1];
B4 = [1 2 4; 1/2 1 3; 1/4 1/3 1];

% 计算准则层权向量
[V2, D2] = eig(A);
W2 = V2(:, 1) / sum(V2(:, 1));
lambda2 = D2(1, 1);

% 准则层一致性检验
CI2 = (lambda2 - size(A, 1)) / (size(A, 1) - 1);
RI = [0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49];
CR2 = CI2 ./ RI(size(A, 1));
if CR2 < 0.1
    disp('准则层一致性检验通过');
    CR2
else
    error('准则层一致性检验不通过');
end

% 计算方案层权向量
[V3_1, D3_1] = eig(B1);
[V3_2, D3_2] = eig(B2);
[V3_3, D3_3] = eig(B3);
[V3_4, D3_4] = eig(B4);
W3_1 = V3_1(:, 1) / sum(V3_1(:, 1));
W3_2 = V3_2(:, 1) / sum(V3_2(:, 1));
W3_3 = V3_3(:, 1) / sum(V3_3(:, 1)); 
W3_4 = V3_4(:, 1) / sum(V3_4(:, 1));
lambda3_1 = D3_1(1, 1);
lambda3_2 = D3_2(1, 1);
lambda3_3 = D3_3(1, 1);
lambda3_4 = D3_4(1, 1);

% 方案层一致性检验
lambda3 = [lambda3_1 lambda3_2 lambda3_3 lambda3_4];
CI3 = (lambda3 - size(B1, 1)) ./ (size(B1, 1) - 1);
CR3 = CI3 ./ RI(size(B1, 1));
if CR3 < 0.1
    disp('方案层一致性检验通过');
    CR3
else
    error('方案层一致性检验不通过');
end

% 组合一致性检验
CR = CR2 + CR3 * W2;
if CR < 0.1
    disp('组合一致性检验通过');
    CR
else
    error('组合一致性检验不通过');
end

% 计算最终权向量
W3 = [W3_1 W3_2 W3_3 W3_4];
W = W3 * W2;

% 输出结果
disp('最终权向量为：');
W

结果：

准则层一致性检验通过
CR2 =
    0.0301

方案层一致性检验通过
CR3 =
    0.0079    0.0079    0.0013    0.0158

组合一致性检验通过
CR =
    0.0390

最终权向量为：
W =
    0.6057
    0.2359
    0.1583

因此，最佳方案为方案 1。