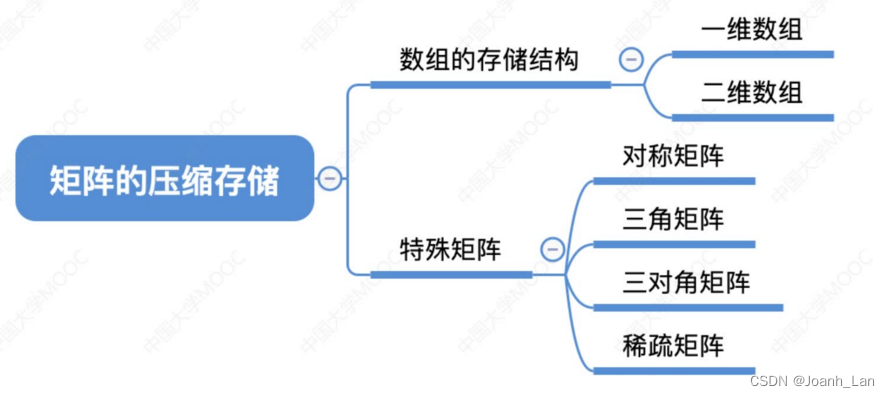
数据结构–特殊矩阵的压缩存储
一维数组的存储结构
ElemType a[10]; //ElemType型一维数组

各数组元素大小相同,且物理上连续存放。
数组元素a[i]的存放地址= LOC + i * sizeof(ElemType)
(
0
≤
i
<
10
)
(0\le i < 10)
(0≤i<10)
注:除非题目特别说明,否则数组
下标默认从
0
开始
\color{red}下标默认从0开始
下标默认从0开始
注意审题
!
易错
!
\color{purple}注意审题!易错!
注意审题!易错!
二维数组的存储结构
ElemType b[2][4];//2行4列的二维数组
逻辑视角 : 逻辑视角: 逻辑视角:
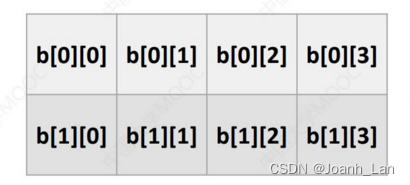
内存视角: 内存视角: 内存视角:
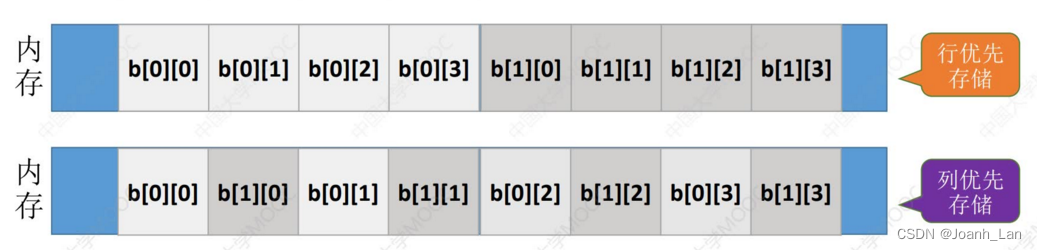
行优先存储

M行N列的二维数组b[M][N]中,若按行优先存储,则b[i][i]的存储地址= LOC+( i * N + j) * sizeof(ElemType)
列优先存储
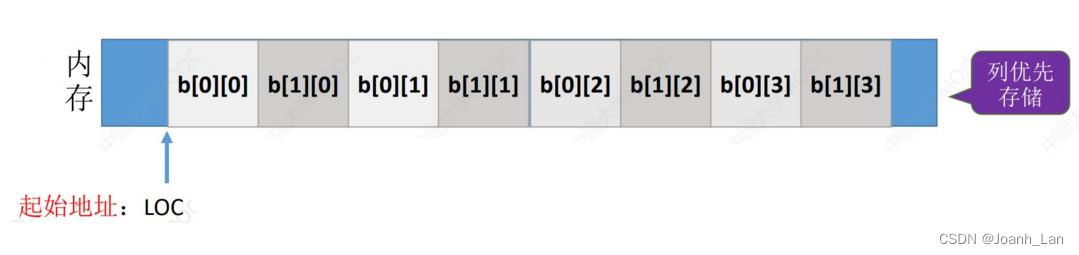
M行N列的二维数组b[M][N]中,若按列优先存储,则b[i][li]的存储地址= LOC+( j * M+ i ) * sizeof(ElemType)
普通矩阵的存储

可用二维数组存储 \color{red}可用二维数组存储 可用二维数组存储
注意:描述矩阵元素时,行、列号通常从1开始;而描述数组时通常下标从0开始
(具体看题目给的条件,注意审题!)
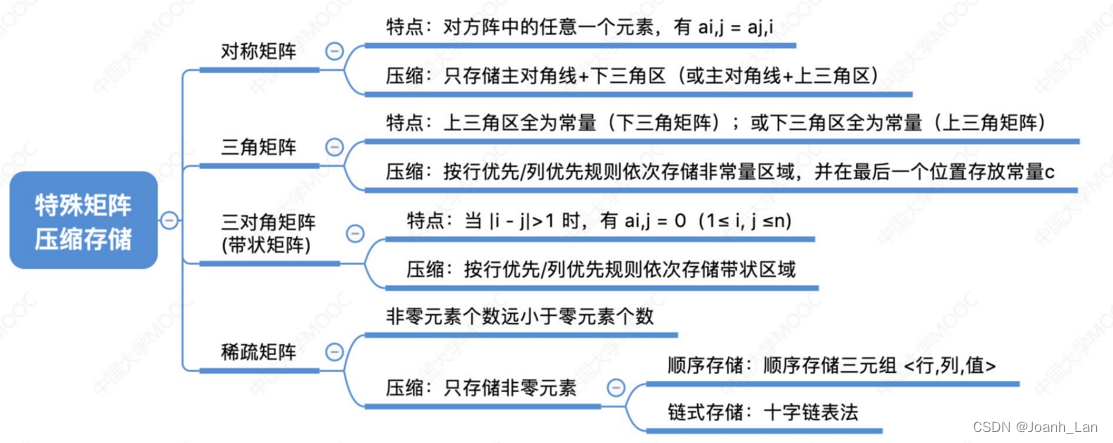
特殊矩阵的存储
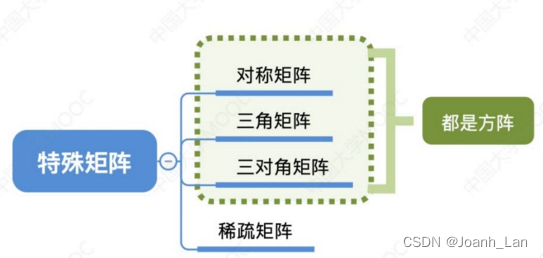
某些特殊矩阵可以压缩存储空间 \color{red}某些特殊矩阵可以压缩存储空间 某些特殊矩阵可以压缩存储空间
对称矩阵的压缩存储
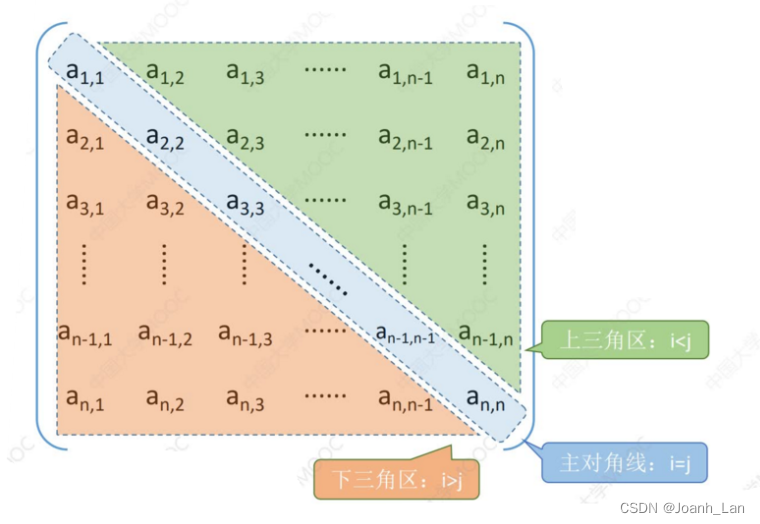
若
n
n
n 阶
方阵
\color{green}方阵
方阵中任意一个元素
a
i
,
j
\color{green}{a_{i,j}}
ai,j ,都有
a
i
,
j
=
a
j
,
i
\color{green}{a_{i,j} = a_{j,i}}
ai,j=aj,i 则该矩阵为对称矩阵
普通存储:
n
∗
n
n*n
n∗n 二维数组
压缩存储策略:只存储主对角线+下三角区(或主对角线+上三角区)
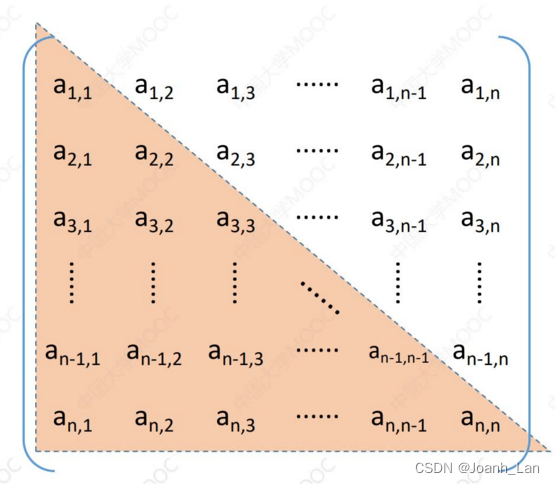
策略
\color{purple}策略
策略:只存储主对角线+下三角区
按
行优先
\color{red}行优先
行优先原则将各元素存入一维数组中。

思考:
①数组大小应为多少?
②站在程序员的角度,对称矩阵压缩存储后怎样才能方便使用?
回答:
①(1+n)*n/2
②可以实现一个“映射”函数:矩阵下标→一维数组下标
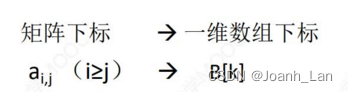
K e y \color{red}Key Key:按 行优先 \color{green}行优先 行优先的原则, a i , j a_{i,j} ai,j 是第几个元素?
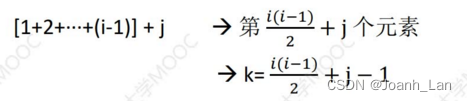

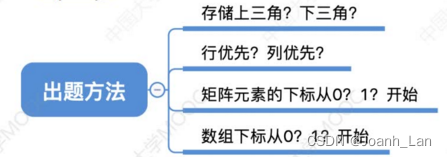
三角矩阵的压缩存储
下三角矩阵:除了主对角线和下三角区,其余的元素都相同

上三角矩阵:除了主对角线和上三角区,其余的元素都相同

下三角矩阵
压缩存储策略:按 行优先 \color{red}行优先 行优先原则将橙色区元素存入一维数组中。并 在最后一个位置存储常量 c \color{red}在最后一个位置存储常量c 在最后一个位置存储常量c

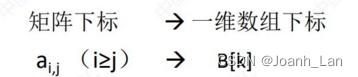
K e y \color{red}Key Key:按 行优先 \color{red}行优先 行优先的原则, a i , j a_{}i,j ai,j是第几个元素?

上三角矩阵
压缩存储策略:按 行优先 \color{red}行优先 行优先原则将绿色区元素存入一维数组中。并 在最后一个位置存储常量 c \color{red}在最后一个位置存储常量c 在最后一个位置存储常量c

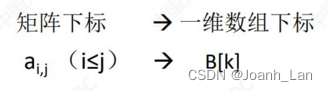
K e y \color{red}Key Key:按 行优先 \color{red}行优先 行优先的原则, a i , j a_{i,j} ai,j是第几个元素?
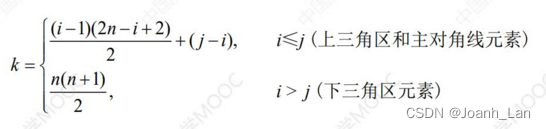
三对角矩阵的压缩存储
三对角矩阵
三对角矩阵
三对角矩阵,又称
带状矩阵
带状矩阵
带状矩阵:
当
∣
i
−
j
∣
>
1
|i-j|>1
∣i−j∣>1时,有
a
i
,
j
=
0
(
1
≤
i
,
j
≤
n
)
a_{i,j}=0 ( 1 \le i, j ≤ n)
ai,j=0(1≤i,j≤n)
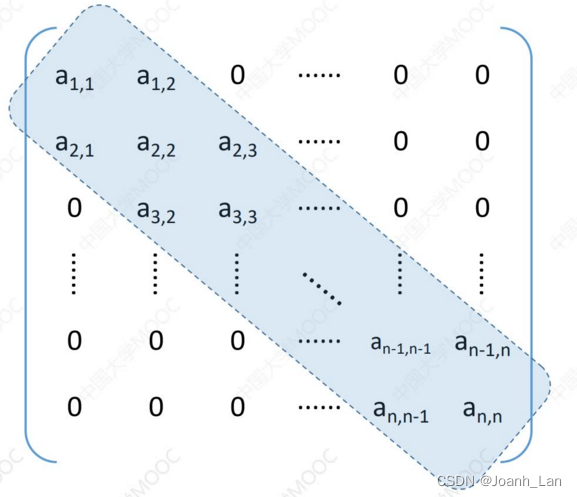
压缩存储策略
:
\color{black}压缩存储策略:
压缩存储策略:
按
行优先
\color{red}行优先
行优先(或列优先)原则,只存储带状部分


K e y \color{red}Key Key:按 行优先 \color{red}行优先 行优先的原则, a i , j a_{i,j} ai,j是第几个元素?

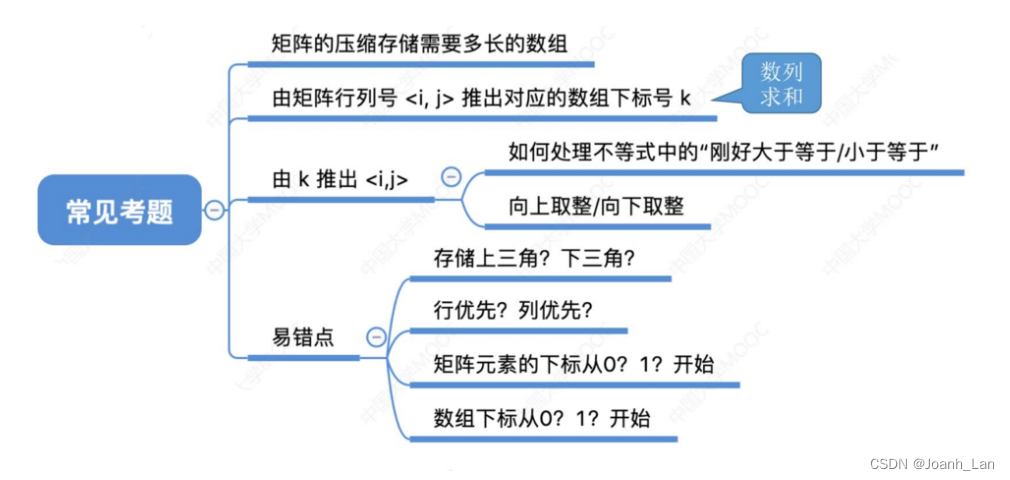
若已知数组下标k,如何得到i, j?
B
[
k
]
→
a
i
,
j
B[k] \to a_{i,j}
B[k]→ai,j
第k+1个元素,在第几行?第几列?
前
i
−
1
i-1
i−1 行共
3
(
i
−
1
)
−
1
3(i-1)-1
3(i−1)−1 个元素
前
i
i
i 行共
3
i
−
1
3i-1
3i−1 个元素
显然,
3
(
i
−
1
)
−
1
<
k
+
1
≤
3
i
−
1
3(i-1)-1<k+1 ≤ 3i-1
3(i−1)−1<k+1≤3i−1
i
≥
(
k
+
2
)
/
3
i ≥ (k+2)/3
i≥(k+2)/3
可以理解为“刚好”大于等于
$i =
⌈
k
+
2
3
⌉
\left\lceil\dfrac{k+2}{3}\right\rceil
⌈3k+2⌉
向上取整即可满足“刚好”大于等于

第k+1个元素,在第几行?第几列?
i =
⌈
(
k
+
2
)
/
3
⌉
\left\lceil(k+2)/3\right\rceil
⌈(k+2)/3⌉
或
i =
⌊
(
k
+
1
)
/
3
+
1
⌋
\left\lfloor(k+1)/3+1\right\rfloor
⌊(k+1)/3+1⌋
由 k = 2 i + j − 3 k = 2i+j-3 k=2i+j−3,得 j = k − 2 i + 3 j = k- 2i+ 3 j=k−2i+3
稀疏矩阵的压缩存储
稀疏矩阵 \color{red}稀疏矩阵 稀疏矩阵:非零元素远远少于矩阵元素的个数
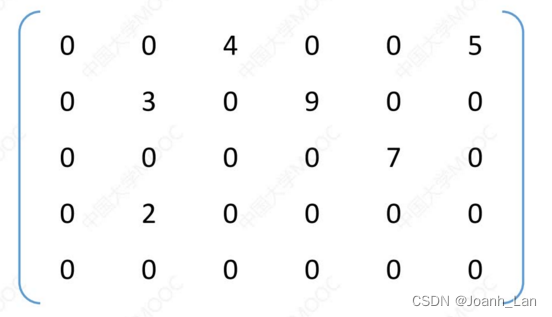
压缩存储策略:
顺序存储 ―― 三元组<行,列,值>
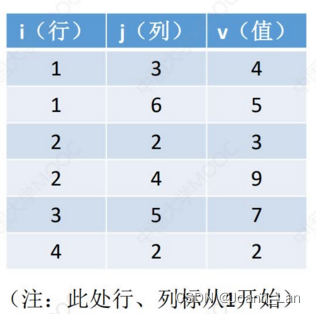
压缩存储策略二:
链式存储――
十字链表法
\color{red}十字链表法
十字链表法

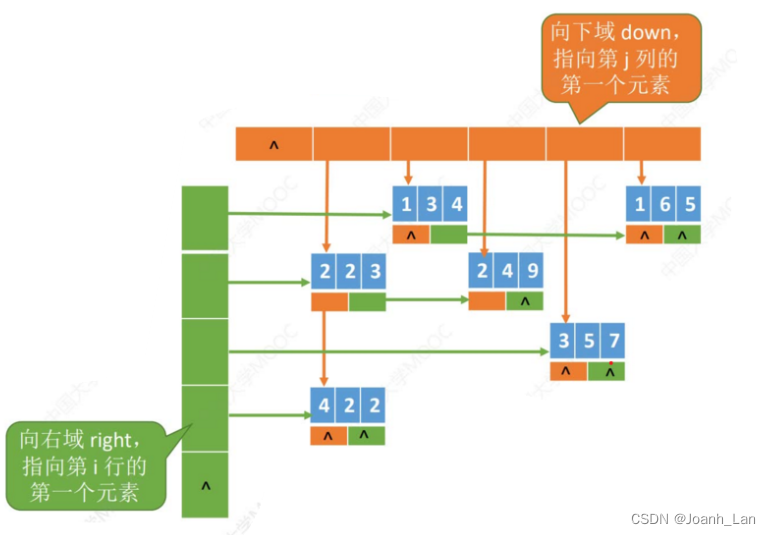
知识点回顾与重要考点