这应该算是很套路的题，照理说是要做出来的

E - MEX (atcoder.jp)

题意：

思路：

首先，三元组很容易让我们联想到枚举中间那个元素，但是在这道题中不是这么搞的

可以注意到，题目是要我们统计所有子序列"MEX"对应的贡献

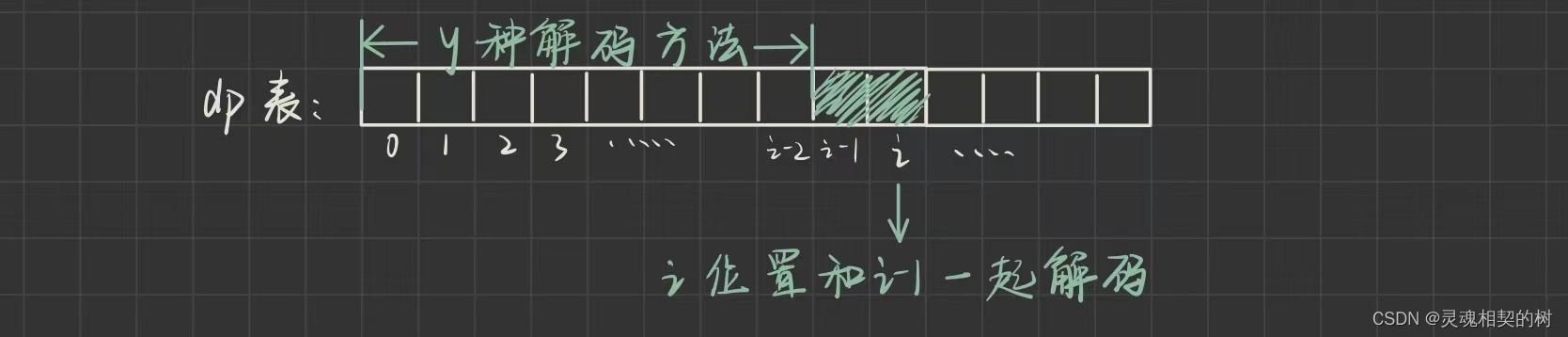
因此我们可以考虑子序列DP

第一维可以表示前M，前ME，前MEX的状态

但是随着每个位置的ai值不同，每个"MEX"子序列的mex贡献也是不一样的，所以我们可以考虑记录所有012排列的mex值，这个可以状压处理一下

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int mxn=2e5+10;
const int Inf=0x3f3f3f3f;

string s;

int N;
int a[mxn],v[10]=
{0,1,0,2,0,1,0,3,0,0};
int dp[4][10];

void solve(){
    cin>>N;
    for(int i=1;i<=N;i++) cin>>a[i];
    cin>>s;
    s=" "+s;
    dp[0][0]=1;
    for(int i=1;i<=N;i++){
        if(s[i]=='M'){
            for(int j=0;j<8;j++){
                dp[1][j|(1<<a[i])]+=dp[0][j];
            }
        }else if(s[i]=='E'){
            for(int j=0;j<8;j++){
                dp[2][j|(1<<a[i])]+=dp[1][j];
            }
        }else{
            for(int j=0;j<8;j++){
                dp[3][j|(1<<a[i])]+=dp[2][j];
            }
        }
    }
    int ans=0;
    for(int j=0;j<8;j++) ans+=dp[3][j]*v[j];
    cout<<ans<<'\n';
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;//cin>>__;
    while(__--)solve();return 0;
}