参考安装

原理：

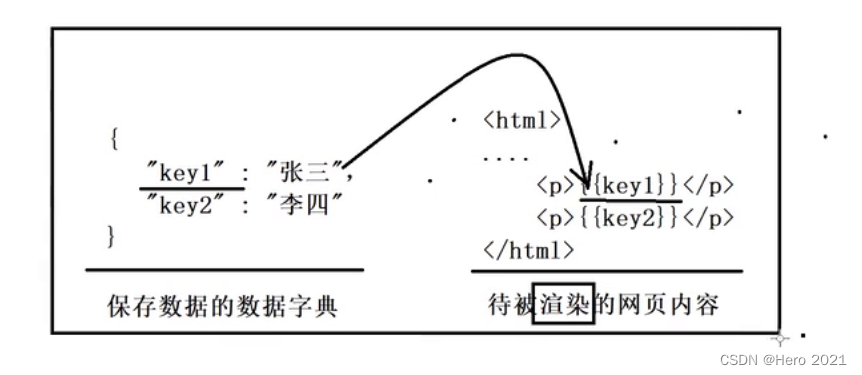
如何使用？

// test_ctemplate.cc
#include <iostream>
#include <string>
#include <ctemplate/template.h>

int main()
{
    std::string in_html = "./test.html";
    std::string value = "一行白鹭上青天";

    // 形成数据字典
    ctemplate::TemplateDictionary root("test"); // 类比定义了一个 unordered_map<> test;
    root.SetValue("key", value);                // 类比 test.insert({key,value});

    // 获取被渲染网页对象
    ctemplate::Template *tpl = ctemplate::Template::GetTemplate(in_html, ctemplate::DO_NOT_STRIP);

    // 添加数据到网页中
    std::string out_html;
    tpl->Expand(&out_html, &root);

    std::cout << out_html << std::endl;
    return 0;
}

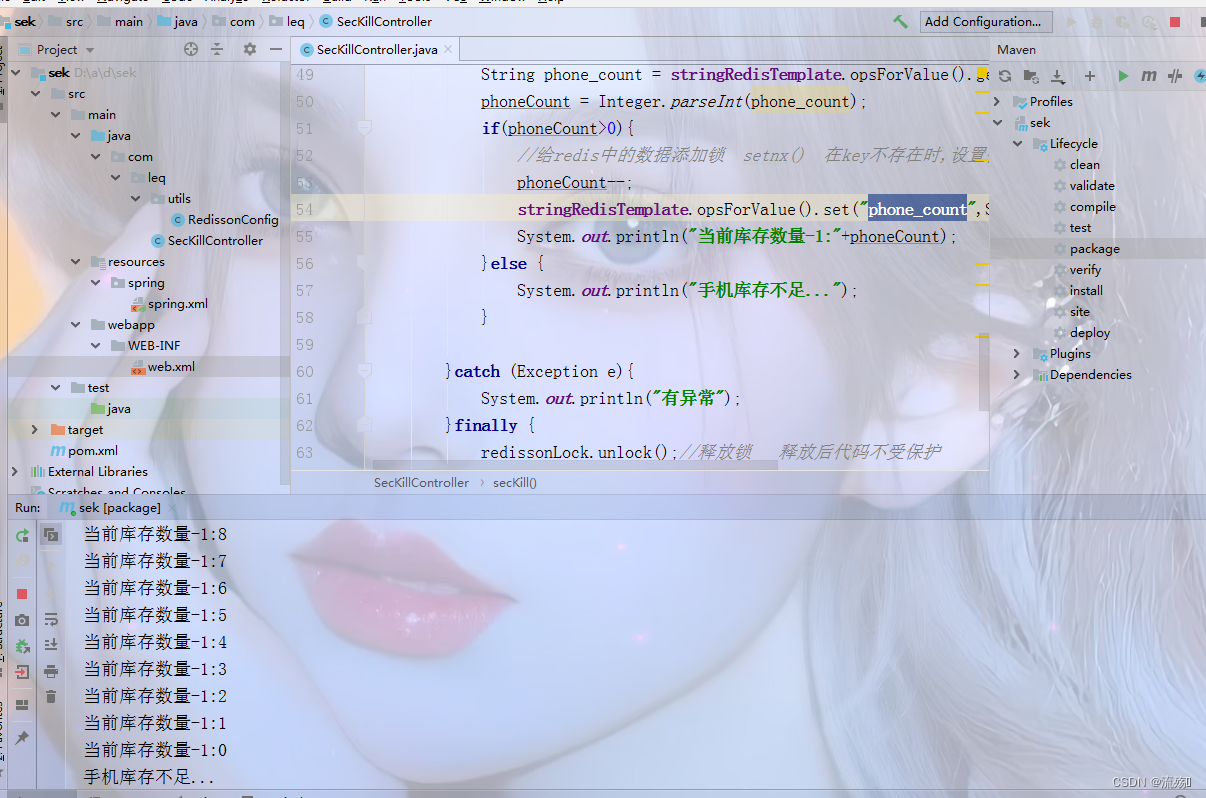
可能会遇到这个问题：

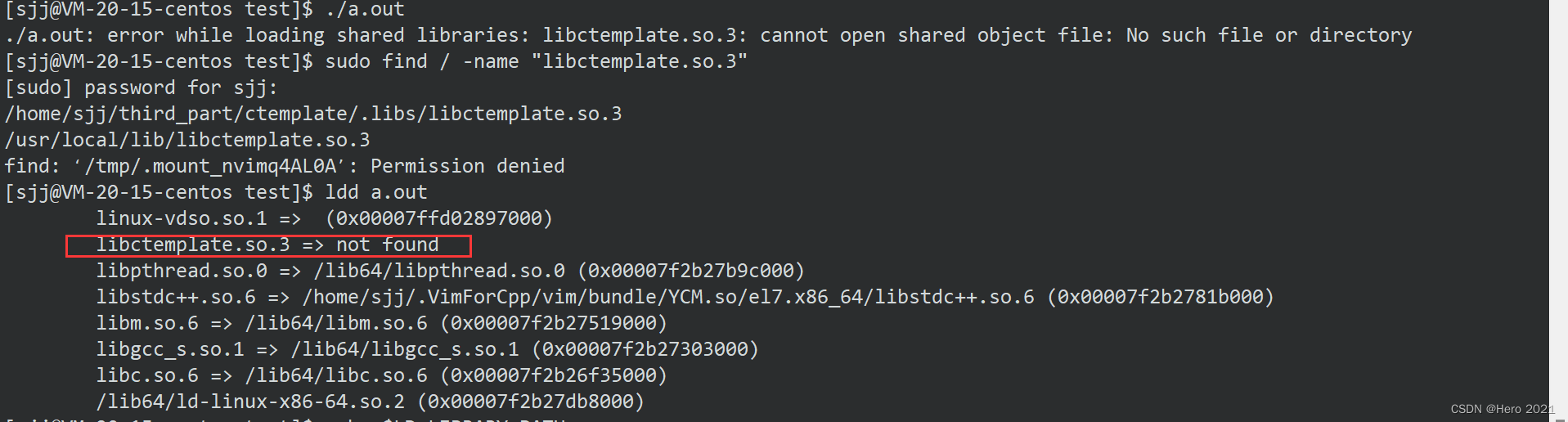
点击这里，这样解决

运行结果：

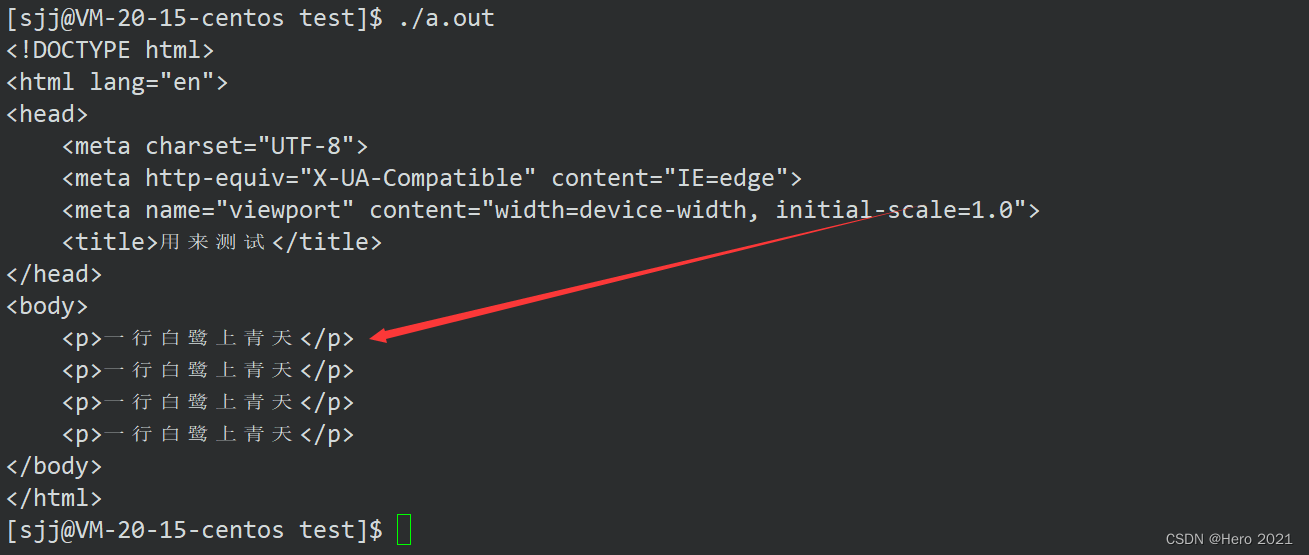
将所有的 {{}} 中的key 替换成了value显示在html中。