本篇总结动态规划中的斐波那契数列模型的解法和思路

按照以下流程进行分析题目和代码编写

思路分析步骤	代码编写步骤
1, 状态表示	1, 构造 dp 表
2, 状态转移方程	2, 初始化+边界处理
3, 初始化	3, 填表(抄状态转移方程)
4, 填表顺序	4, 返回结果
5, 返回值	/

---

一、第 N 个泰波那契数

1, 题目

OJ链接

题目分析: 第 N 个数 = 第 N-1 个数 + 第 N-2 个数 + 第 N-3 个数

---

2, 思路分析

2.1, 状态表示

根据题目要求, 要我们算出第 N 个数是多少, 我们要构造一个dp表(数组), 表中的值就是第 N 个数的值

所以对于整个数列来说, 对于 i(任意数) 位置, 都可以表示成 dp[i]

状态表示 : dp[i] 就是第 i 个泰波那契数

---

2.2, 状态转移方程

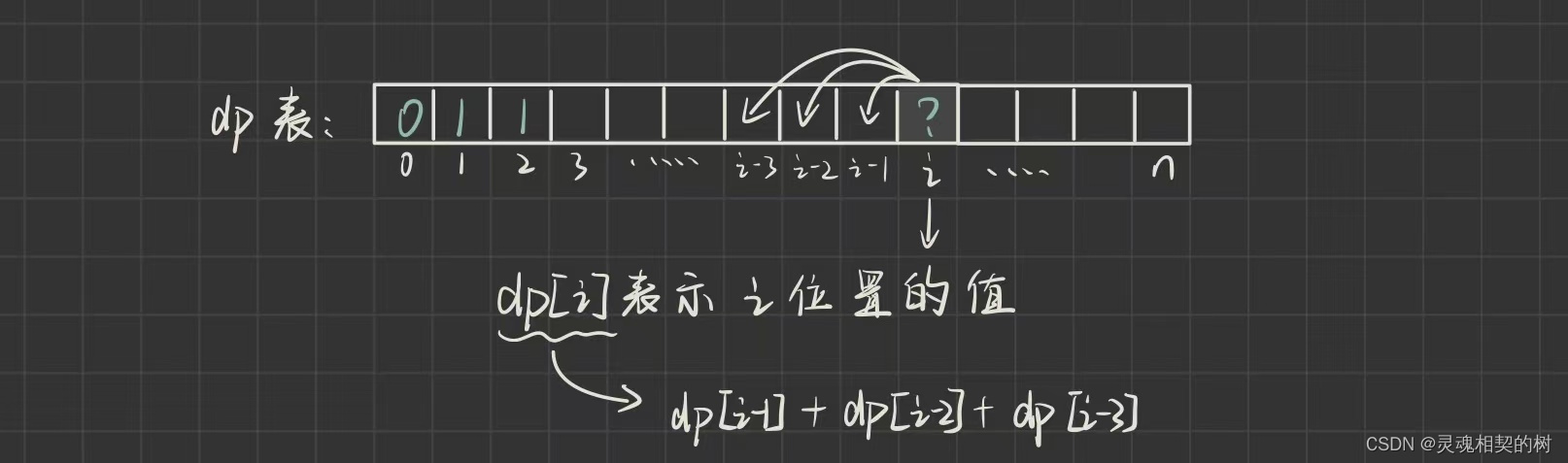
根据 : 第 N 个数 = 第 N-1 个数 + 第 N-2 个数 + 第 N-3 个数 可直接得出

状态转移方程 : dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]

---

2.3, 初始化

初始化是为了填表的时候不越界访问

根据状态转移方程可以分析出, dp[i] 依赖前三个数的值, 所以在表中前三个数的值必须手动填, 从第四个数开始可以根据状态转移方程来填

题中已经告诉我们 dp[0] = 0, dp[1] = dp[2] = 1

---

2.4, 填表顺序

由于dp[i] 依赖前三个数的值, 所以在确定任意位置的值时, 首先要知道前三个数的值, 所以填表顺序是从左往右

---

2.5, 返回值

要我们求第 N 个数的值, 就是 dp[N]

要访问 dp[N] , dp 表的长度是多少?

---

3, 代码

在构造 dp 表时, int[] dp = new int[n];是错的, 长度为 n 的数组, 下标是 0 ~ n-1, 要想访问到 dp[n], dp 表的长度应该是 n + 1

public int tribonacci(int n) {
        // 1, 构造dp表
        int[] dp = new int[n + 1];
        // 2, 初始化 + 边界条件判断
        if(n == 0 || n == 1) {
            return n;
        }
        if(n == 2) {
            return 1;
        }
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 1;
        // 3, 填表(抄状态转移方程)
        for(int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];            
        }
        // 4, 返回值
        return dp[n];
    }

---

二、三步问题

1, 题目

OJ链接

分析题目得知, 在第 N 个台阶时, 可以从第 N - 1 个台阶跳一个台阶上来, 可以从第 N - 2 个台阶跳两个台阶上来, 可以从第 N - 3 个台阶跳三个台阶上来

---

2, 思路分析

2.1, 状态表示

根据题目要求可知, 在 dp 表中的值就是到达某个台阶时的跳法总数

状态表示 : dp[i] 就是到达第 i 个台阶时, 跳法的总数

---

2.2, 状态转移方程

以 i 位置状态的最近的⼀步，来分情况讨论, 要求 dp[i], 已经分析过有三种情况

• 在第 i - 1 个台阶时, 有 ? 种跳法, 加一步即可
• 从第 i - 2 个台阶时, 有 ? 种跳法, 加一步即可
• 从第 i - 3 个台阶时, 有 ? 种跳法, 加一步即可

所以在第 i 个台阶时的跳法总数就是 : 上述三个状态的跳法总数的和

状态转移方程 : dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]

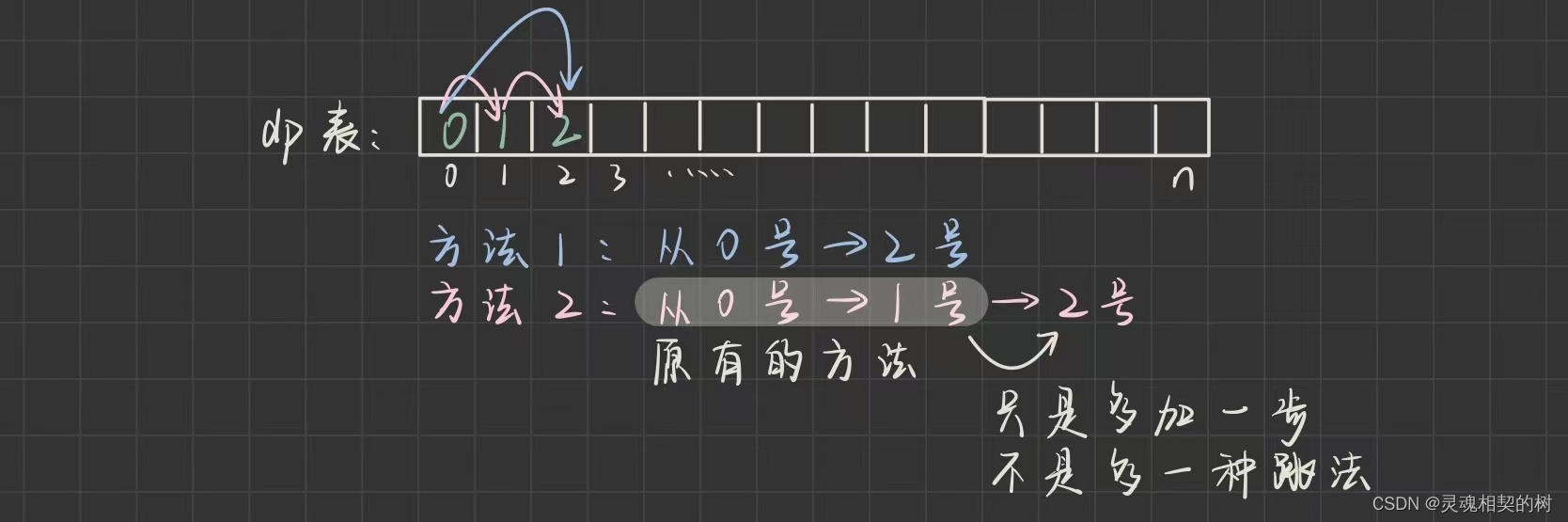
问 : 为什么不是 dp[i] = dp[i - 1] + 1 + dp[i - 2] + 1 + dp[i - 3] + 1 呢? 不是多跳了一步吗?
答 : 是多跳了一步, 但只是在原有的跳法上多跳了一下, 并没有产生新的跳法!!! 这一点一定要理解, 我们求的是有多少种跳法, 而不是跳了多少步!!

实在不理解可以带入第二个台阶, 进行分析

---

2.3, 初始化

初始化是为了填表的时候不越界访问

根据状态转移方程可以分析出, dp[i] 依赖前三个数的值, 所以在表中前三个数的值必须手动填, 从第四个数开始可以根据状态转移方程来填

可以简单推导出 dp[1] = 1, dp[2] = 2, dp[3] = 4;

我们让 0 号台阶表示地平线, 不需要给 dp[0] 赋值, 没有意义

---

2.4, 填表顺序

由于dp[i] 依赖前三个数的值, 所以在确定任意位置的值时, 首先要知道前三个数的值, 所以填表顺序是从左往右

---

2.5, 返回值

要我们求第 N 个数的值, 就是 dp[N]

要访问 dp[N] , 初始化时 dp 表的长度是多少?

---

3, 代码

在构造 dp 表时, int[] dp = new int[n];是错的, 长度为 n 的数组, 下标是 0 ~ n-1, 要想访问到 dp[n], dp 表的长度应该是 n + 1

	public int waysToStep(int n) {
        // 1, 构造dp表
        int[] dp = new int[n + 1];
        // 2, 初始化+边界条件处理
        if(n <= 2) {
            return n;
        }
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 4;
        // 3, 填表(抄状态转移方程)
        for(int i = 4; i <= n ; i++) {
            dp[i] = ((dp[i - 1]  + dp[i - 2]) % 1000000007 +  dp[i-3]) % 1000000007;
        }
        // 4, 返回值
        return dp[n];
    }

---

三、

1, 题目

OJ链接

分析题目得知, 要达第 N 个台阶, 可以从第 N-1个台阶过来, 也可以从第 N-2 个台阶过来, 如果 cost 数组的长度为 n , 台阶数为 n - 1, 因为 cost[0] 表示从地平线起跳要支付的费用, 楼顶在 n 的位置

---

2, 思路分析

2.1, 状态表示

我们需要构造 dp 表, 要求到达楼顶的最小花费, 需要先知道中途到达任意位置的最小花费(划分子问题), 所以 状态表示 : dp[i] 就是以 i 为终点, 到达 i 位置的最小花费

---

2.2, 状态转移方程

以 i 位置状态的最近的⼀步，来分情况讨论, 要求 dp[i](到达 i 位置的最小花费), 有两种情况

• 从第 i - 1 位置上来 : 在此位置的最小花费 + 从此位置起跳要支付的费用
• 从第 i - 2 位置上来 : 在此位置的最小花费 + 从此位置起跳要支付的费用

要保证到达 i 位置时花费的钱最少, 就要对这两种方式的费用取较小值

注意题中给的 cost 数组和 dp 数组的关系 :

状态转移方程 : dp[i] = min (dp[i - 1] + cost[i- 1], dp[i - 2] + cost[i- 2])

---

2.3, 初始化

初始化是为了填表的时候不越界访问

根据状态转移方程可知, 填 dp 表中的值, 依赖前两个位置的值, 所以在 dp 表中, 0 下标和 1 下标必须初始化

题目已经说明, 可以自由选择从 0 号台阶或 1 号台阶起跳, 所以到达 0 号台阶或 1 号台阶的最小花费为 0 元, 所以 : dp[0] = 0, dp[1] = 0;

---

2.4, 填表顺序

dp[i] 的值依赖前两个位置的值, 所以填表顺序是从左往右

---

2.5, 返回值

cost 长度为 N, 则有 N - 1 个台阶, 楼顶在 N 位置, 所以返回 dp[N]

要访问 dp[N] , 初始化时 dp 表的长度是多少?

---

3, 代码

在构造 dp 表时, int[] dp = new int[n];是错的, 长度为 n 的数组, 下标是 0 ~ n-1, 要想访问到 dp[n], dp 表的长度应该是 n + 1

	public int minCostClimbingStairs(int[] cost) {
        // 构造dp表
        int n = cost.length;
        int[] dp = new int[n + 1];
        // 初始化+边界条件
        dp[0] = 0;
        dp[1] = 0;
        // 填表(抄状态转移方)
        for(int i = 2; i <= n ;i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i  -1], dp[i - 2] + cost[i - 2]) ;
        }
        // 返回值
        return dp[n];
    }

---

四、

1, 题目

OJ链接

---

2, 思路分析

2.1, 状态表示

状态表示 : dp[i] 就是以 i 位置为结尾, 编码方法的总数

---

2.2, 状态转移方程

以 i 位置状态的最近的⼀步，来分情况讨论, 要求 dp[i], 有两种方式 :

• i 位置的数字单独解码, 如果解码成功, dp[i] 加上 x , (从0 到 i - 1位置的所有解码方法总数)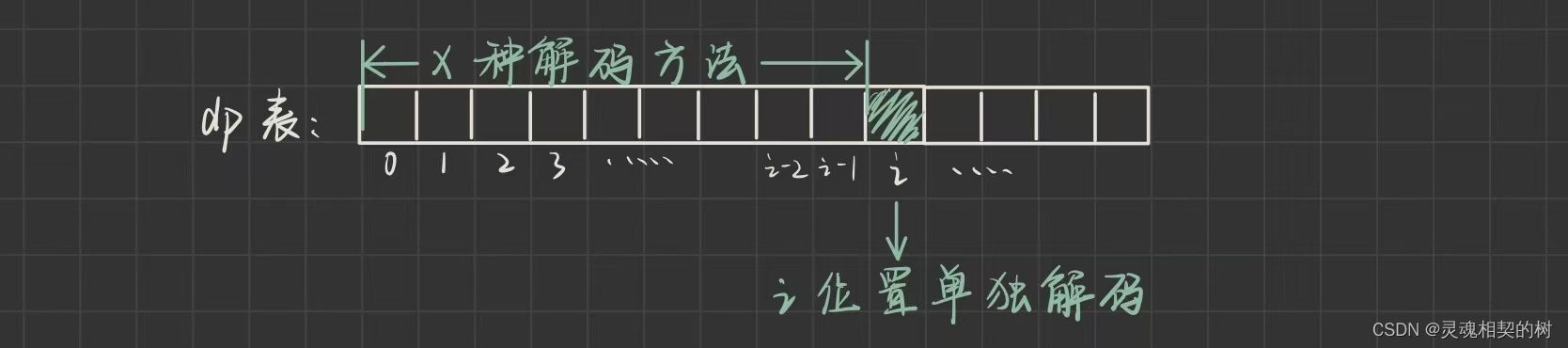

• i 位置的数字和 i - 1 位置的数字一起解码, 如果解码成功, dp[i] 加上 y , (从0 到 i - 2位置的所有解码方法总数)
  

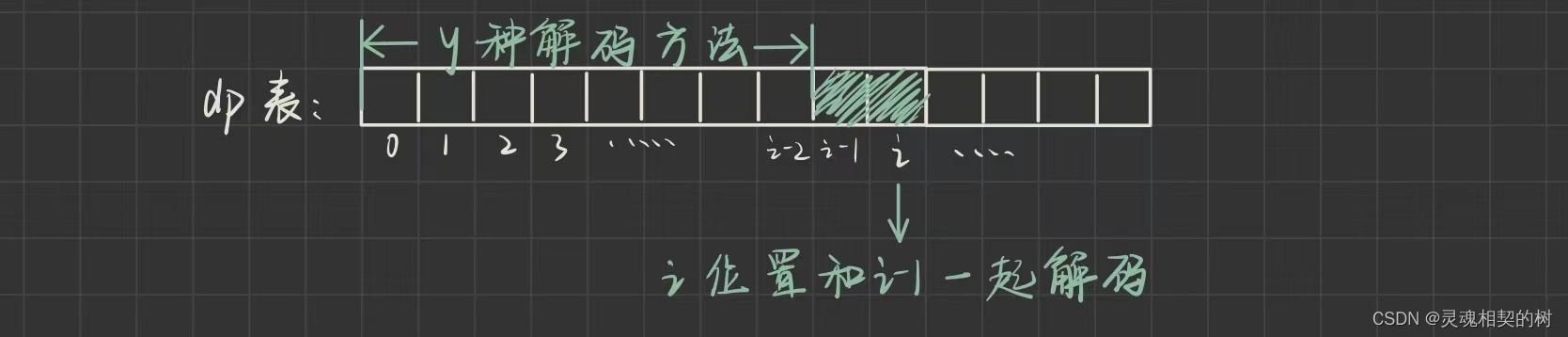
结合状态表示可知 : x = 从0 到 i - 1位置的所有解码方法总数 = dp[i- 1], y = 从0 到 i - 1位置的所有解码方法总数 = dp[i- 2]

所以状态转移方程 : 如果方案一成功, dp[i] += dp[i-1], 如果方案二成功, dp[i] += dp[i-2],

这里千万要搞清楚, 无论哪种方式解码, 都在只是增加了解码的字符串长度, 而不是新增了一种解码方式

无论哪种方式解码, 一旦解码失败, dp[i] += 0 即可, 如果当前位置的解码方式为 0, 计算到下一个位置时, 会依赖当前位置的 dp 值, 所以后面 dp 表中的值都为 0, 最终返回结果为 0

---

2.3, 初始化

初始化是为了填表的时候不越界访问

根据状态转移方程可知, 填表到某一位置时, 依赖前两个位置的值, 所以初始化dp表中 0 下标和 1 下标即可

---

2.4, 填表顺序

填表顺序是从左往右

---

2.5, 返回值

要求的是整个字符串的解码方案总数, 令字符串长度为 n, 返回dp[n - 1]

---

3, 代码

    public int numDecodings(String s) {
        // 构造 dp 表
        int n = s.length();
        int[] dp = new int[n];
        char[] array = s.toCharArray();
        // 初始化+边界条件
        if(array[0] != '0') {
            dp[0] = 1;
        }
        if(n == 1) {
            return dp[0];
        }
        if( array[1] != '0') {
            dp[1] += dp[0];
        }
        int num = (array[0] -'0') * 10 + (array[1]-'0');
        if( num >= 10 && num <= 26 ) {
            dp[1] += dp[0];
        }
        // 填表(抄状态转移方程)
        for(int i = 2; i < n; i++) {
            if(array[i] != '0') {
                dp[i] += dp[i - 1];
            }
            num = (array[i-1] -'0') * 10 + (array[i]-'0');
            if( num >= 10 && num <= 26 ) {
                dp[i] += dp[i - 2];
            }
        }
        // 返回值
        return dp[n - 1];
    }

---