一、算法灵感

白鲸优化算法(Beluga whale optimization, BWO)是2022年提出的一种元启发式优化算法，其灵感来源于白鲸的生活行为。白鲸以成年鲸的纯白色而闻名，是高度群居的动物，它们可以成群聚集，有2到25个成员，平均有10个成员。与其他元启发式方法类似，BWO包含探索阶段和开发阶段，此外该算法还模拟了生物界中存在的鲸落现象。

二、算法介绍

2.1 初始化

探索阶段通过随机选择白鲸，保证了设计空间中的全局搜索能力，开发阶段控制着设计空间中的局部搜索。为了模拟行为，白鲸被视为搜索代理，通过改变位置向量在搜索空间中移动。此外，在BWO中考虑了鲸鱼坠落的概率，它改变了白鲸的位置。
由于BWO基于种群的机制，白鲸被视为搜索代理，而每条白鲸都是一个候选解决方案，并在优化过程中进行更新。矩阵到搜索代理位置的矩阵被建模为：
$X{\rm{ = }}\left[ \begin{aligned} {{x_{1,1}}} & {{x_{1,2}}} & {...} & {{x_{1,d}}} \cr {{x_{2,1}}} & {{x_{2,2}}} & {...} & {{x_{2,d}}} \cr \vdots & \vdots & \vdots & \vdots \cr {{x_{n,1}}} & {{x_{n,2}}} & {...} & {{x_{n,d}}} \cr \end{aligned} \right]\tag{1}$ 其中， $n$ 为白鲸的种群大小， $d$ 为设计变量的维数。对于所有的白鲸，相应的适应度值存储如下：
${F_X} = \left[ \begin{aligned} {f({x_{1,1}},{x_{1,2}},...,{x_{1,d}})} \cr {f({x_{2,1}},{x_{2,2}},...,{x_{2,d}})} \cr \vdots \cr {f({x_{n,1}},{x_{n,2}},...,{x_{n,d}})} \cr \end{aligned} \right]\tag{2}$ BWO算法可以从探索转向开发，这取决于平衡因子 $B_f$ ，其数学模型为：
${B_f} = {B_0}(1 - {t \over {2T}})\tag{3}$ 其中， $t$ 为当前迭代， $T$ 为最大迭代数， $B_0$ 在每次迭代时在 $(0, 1)$ 之间随机变化。勘探阶段发生在平衡因子 $B_f>0.5$ ，而开发阶段发生在 $B_f$ ≤0.5。随着迭代 $T$ 的增加， $B_f$ 的波动范围从 $(0, 1)$ 减小到 $(0, 0.5)$ ，说明开发和勘探阶段的概率发生了显著变化，而开发阶段的概率随着迭代 $T$ 的不断增加而增加。

2.2 探索阶段

BWO的探索阶段是通过考虑白鲸的游泳行为来建立的。白鲸可以在不同的姿势下进行社会性行为，如两对白鲸以同步或镜像的方式紧密地游泳。因此，搜索代理的位置由一对白鲸的游泳决定，白鲸的位置更新如下：
$\left\{ \begin{aligned} &X_{i,j}^{t + 1} = X_{i,{p_j}}^t + (X_{r,{p_1}}^t - X_{i,{p_j}}^t)(1 + {r_1})sin(2\pi {r_2})&&,j=even \cr &X_{i,j}^{t + 1} = X_{i,{p_j}}^t + (X_{r,{p_1}}^t - X_{i,{p_j}}^t)(1 + {r_1})\cos (2\pi {r_2})&&,j= odd \cr \end{aligned} \right.\tag{4}$ 其中， $t$ 为当前迭代次数， $X_{i,j}^{t + 1}$ 是第 $i$ 条白鲸在第 $j$ 维上的新位置， ${P_j}(j = 12...,d)$ 是从 $d$ 维中随机选择的， $X_{i,j}^t$ 是第 $i$ 条白鲸在 $j$ 维度上的位置， $X_{i,{p_j}}^t$ 和 $X_{r,{p_1}}^t$ 是第 $i$ 和第 $r$ 条白鲸( $r$ 代表随机选择的白鲸)的当前位置， $r_1$ 和 $r_2$ 是范围在 $(0, 1)$ 的随机数，用于增强勘探阶段的随机算子。 $sin(2πr_2)$ 和 $cos(2πr_2)$ 用于平均鱼鳍之间的随机数。根据奇数和偶数选择的维度，更新后的位置反映了白鲸在游泳或潜水时的同步或镜像行为。

2.3 开发阶段

BWO的开发阶段的灵感来自于白鲸的捕食行为。白鲸可以根据相邻白鲸的位置，合作觅食和移动。因此，白鲸通过分享彼此的位置信息来猎物，考虑最好的候选解和其他解。在BWO的开发阶段引入了Levy飞行的策略，以提高收敛性。我们假设它们可以用Levy飞行策略捕捉猎物，其数学模型表示为：
$X_i^{t + 1} = {r_3}X_{best}^t - {r_4}X_i^t + {C_1} \cdot {L_F} \cdot (X_r^t - X_i^t)\tag{5}$ 其中， $T$ 为当前迭代次数， $X_i^t$ 和 $X_r^t$ 是第 $i$ 条白鲸和一条随机的白鲸的当前位置， $X_i^{t + 1}$ 是第 $i$ 条白鲸的新位置， $X_{best}^t$ 是鲸鱼中最佳位置， $r_3$ 和 $r_4$ 是范围在 $(0, 1)$ 的随机数， ${C_1} = 2{r_4}(1 - t/{T_{max}})$ 用于测量Levy飞行强度的随机跳跃强度。
$L_F$ 为Levy飞行函数，其计算方法如下：
${L_F} = 0.05 \times {{u \times \sigma } \over {{{\left| v \right|}^{1/\beta }}}}\tag{6}$ $\sigma = {\left( {{{\Gamma (1 + \beta ) \times sin(\pi \beta /2)} \over {\Gamma ((1 + \beta )/2) \times \beta \times {2^{(\beta - 1)/2}}}}} \right)^{1/\beta }}\tag{7}$ 其中， $u$ 和 $v$ 是正态分布的随机数， $β$ 是默认的常数，等于 $1.5$ 。

2.4 鲸落阶段

在迁徙和觅食的过程中，白鲸受到了来自虎鲸、北极熊和人类的威胁。大多数白鲸都很聪明，可以通过彼此分享信息来逃避威胁。然而，少数白鲸没有幸存下来，掉进了海底。这种现象被称为“鲸鱼坠落”，喂养了大量的生物。大量的鲨鱼和无脊椎动物聚集在一起喂养鲸鱼的尸体，暴露的死鲸鱼的骨头和尸体吸引了大量的毛发甲壳类动物。最后，骨骼被细菌和珊瑚分解或占据了几十年。
为了模拟每次迭代中鲸落的行为，我们选择鲸鱼从种群中掉落的概率作为我们主观的假设，以此模拟群体中的微小变化。我们假设这些白鲸要么转移到其他地方，要么被击落并掉入深海。为了保证种群数量不变，我们利用白鲸的位置和鲸鱼下降的步长来建立更新的位置。该数学模型表示为：
$X_i^{t + 1} = {r_5}X_i^t - {r_6}X_r^t + {r_7}{X_{step}}\tag{8}$ 其中， $r_5$ 、 $r_6$ 和 $r_7$ 是 $(0, 1)$ 之间的随机数， $X_{step}$ 是鲸鱼坠落的步长，确定为：
${X_{step}} = ({u_b} - {l_b})exp( - {C_2}{t \over T})\tag{9}$ 其中， $C_2$ 为与鲸鱼下降概率和种群大小相关的步长因子( $C_2=2W_f ×n$ )， $u b$ 和 $l b$ 分别为变量的上界和下界。可以看出，步长受设计变量、迭代次数和最大迭代数的边界的影响。
在这个模型中，鲸鱼坠落的概率( $W_f$ )被计算为一个线性函数：
${W_f} = 0.1 - 0.05t/T\tag{10}$ 鲸鱼坠落的概率从初始迭代的 $0.1$ 下降到最后一次迭代的 $0.05$ ，说明当白鲸在优化过程中更接近食物源时，白鲸的危险降低。

三、改进的白鲸优化算法

3.1 集体行动策略

白鲸是高度社会化的动物，捕食与迁徙等行为都是由团体所共同完成的。白鲸的声音种类繁多，甚至可以在水面上听到。它们使用许多不同的咔嗒声、啁啾声和口哨声（范围从 3-9 kHz）相互交流，但它们也使用非常独特的“铃铛音”，这是只有这种鲸鱼独有的。它们能够借助其自身独特的声音来从而共享自身所在的位置，同时躲避天敌虎鲸。因为鲸鱼的食量很大，在捕食的同时不能与同伴的位置相隔太近，否则会导致获取的食物不够。但是也不能相隔太远，否则会受到来自天敌虎鲸的威胁。本文选用Wk作为临界值来达到既能满足自己食物的需要同时也能尽量减少来自天敌虎鲸的威胁，同时随着迭代次数的增加，搜索代理白鲸也会逐步成长，Wk也会随着迭代次数的增加而增加，Wk的表达式如(11)所示，Wt为白鲸之间的最小距离，本文中定为0.35。同时我们也假设它们可以用Levy飞行策略捕捉猎物，其数学模型表示为：
${W_K} = {t \over {5T}} + {W_t}\tag{11}$ $X_i^{t{\rm{ + 1}}}{\rm{ = }}X_i^t{\rm{ + }}{L_F} \cdot X_{best}^t - {W_K} \cdot (X_r^t{\rm{ + }}X_i^t))\tag{12}$ 其中T为当前迭代次数， $X_i^t$ 和 $X_r^t$ 是第i条白鲸和一条随机的白鲸的当前位置， $X_i^{t + 1}$ 是第i条白鲸的新位置， $X_{best}^t$ 是鲸鱼中最佳位置。
在这里插入图片描述

Figure 1. 策略执行之前

在这里插入图片描述

Figure 2. 策略执行之后

3.2 小孔成像策略

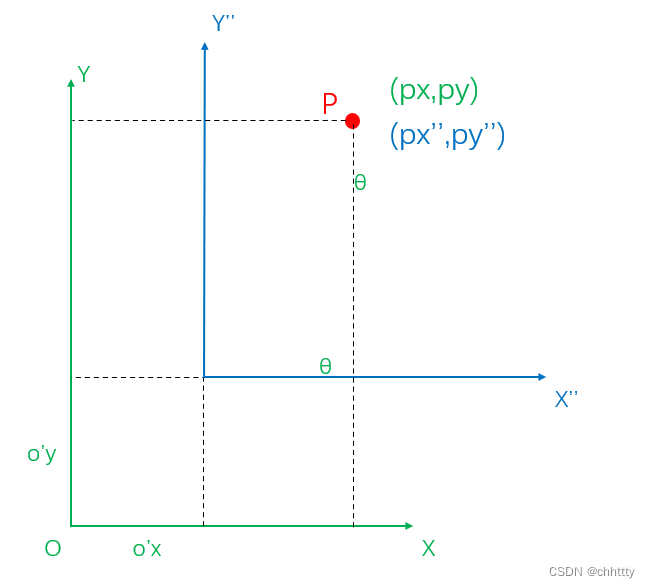
如果种群个体在当前位置的相反位置产生一个相反的个体，则这两个个体就更容易接近最优解，因此只需要进行少量的操作就能起到不错的效果。2005年，Tizhoosh提出了反向学习策略，其原理为根据已知解,生成一个反向解,对比反向解,选择更好的解。Dynamic pinhole imaging strategy是2022年由Li提出的一种通用策略，模仿了光学中的针孔成像理论。与普通的反向学习策略相比，针孔成像理论更准确，可以产生更多样化的对应点。图3为一个典型的针孔成像理论模型。将其应用于总体的搜索空间，可以得到以下数学模型：
${{Xbest_{_{i,j}}^t - (U{b_{i,j}} + L{b_{i,j}})/2} \over {(U{b_{i,j}} + L{b_{i,j}})/2 - X_{_{i,j}}^{t{\rm{ + }}1}}} = {{{L_p}} \over {{L_{ - p}}}}\tag{13}$ 式中为 $Xbest_{_{i,j}}^t$ 当前最佳个体的位置， $X_i^{t + 1}$ 为针孔成像理论中的相反位置。Ubi,j和Lbi,j是第i条白鲸在j维上的动态边界，Lp和L-p分别是虚拟蜡烛在当前最佳位置和相反位置的长度。值得注意的是，虚拟蜡烛在海洋中的位置也是搜索代理的位置，但代表单个鲸鱼的点并没有一个有效长度。因此，两个蜡烛的比例可以设置为一个变量K。由此可知，可以得到：
$X_{_{i,j}}^{t{\rm{ + 1}}} = {{(K + 1)(U{b_{i,j}} + L{b_{i,j}}) - 2Xbest_{_{i,j}}^t} \over {2K}}\tag{13}$ 当两支虚拟蜡烛的长度相同时，这种策略就会演变成一种基本的反向学习策略。适当调整K的值可以改变相反点的位置，使单个白鲸有更多的搜索机会。在本文中，K被设为1.5×104。这样，每次迭代时，都会在搜索空间的中心线附近产生一个新的相反点。当对方的位置较好时，它的位置将成为一个新的边界。
在这里插入图片描述

Fig. 3 Dynamic pinhole imaging strategy

3.3 二次插值策略

二次插值法是一种用于在确定初始区间中搜索极值点的方法,是一种曲线拟合方法。其利用目标函数在若干点的信息构成一个与目标函数值相近的低次多项式,再用此式的最优解作为函数的近似最优解,随着区间的逐步缩短,多项式的最优解与原函数的最优点之间的距离逐步减小,最后满足一定精度要求为止。其原理如图4所示。
利用目标函数在不同3点的函数值构成一个与原函数f(x)相近似的二次多项式p(x),以函数p(x)的极值点(即p(x)=0的根)作为目标函数f(x)近似极值点。设目标函数的单峰区间为x1,x3，函数在x1，x2，x3三点处函数值分别为f1，f2，f3。
$\left\{ \begin{aligned} p({x_1}) = {a_0} + {a_1}{x_1} + {a_2}x_1^2 = {f_1} \cr p({x_2}) = {a_0} + {a_1}{x_2} + {a_2}x_2^2 = {f_2} \cr p({x_3}) = {a_0} + {a_1}{x_3} + {a_2}x_3^2 = {f_3} \cr \end{aligned} \right.\tag{15}$ p(x)的极值点为：
${a_1} + 2{a_2}x = 0\tag{16}$ 求得系数a1,a2,a3的值并代入(15)(16)式可得：
$x_p^* = {{(x_2^2 - x_3^2){f_1} + (x_3^2 - x_1^2){f_2} + (x_1^2 - x_2^2){f_3}} \over {2({x_2} - {x_3}){f_1} + ({x_2} - {x_1}){f_2} + ({x_1} - {x_2}){f_3}}}\tag{17}$ 将公式(17)求得的结果代入目标函数f(x)可得函数值为fp假若f(x)本身就为二次函数，则按照公式(17)上进行求值就能找到最优点。若f(x)为高于二次的函数或者为其他函数，则需要逐步缩小区间。如图4所示，黑实线f(x)的函数图像，蓝虚线为p(x)的函数图像。
在这里插入图片描述

(a)第一次迭代 (b)第二次迭代 Fig. 4 Principle of quadratic interpolation

本文在每一次白鲸位置更新时,将选择最优个体 $Xbest_{_{i,j}}^t$ 与其他两个随机个体 $X_{_{rl}}^t$ 和 $X_{_{rr}}^t$ ,构成一个与目标函数值相近的低次多项式，利用该式求出解 $X_{_{i,j}}^{T + 1}$ ，将上述变量代入到公式(17)即可得到如下公式(18)：
$X_{_{i,j}}^{t + 1} = {1 \over 2} \times {{[(X{{_{_{rl,j}}^t}^2} - Xbest_{_{i,j}}^t)f(X_{_{rr}}^t) + (Xbest_{_{i,j}}^t - X{{_{_{rr,j}}^t}^2})f(X_{_{rl}}^t) + (X{{_{_{rr,j}}^t}^2} - X{{_{_{rl,j}}^t}^2})f(Xbest_{_{i,j}}^t)]} \over {[(X_{_{rl,j}}^t - Xbest_{_{i,j}}^t)f(X_{_{rr}}^t) + (Xbest_{_{i,j}}^t - X_{_{rr,j}}^t)f(X_{_{rl}}^t) + (X_{_{rr,j}}^t - X_{_{rl,j}}^t)f(Xbest_{_{i,j}}^t) + eps]}}\tag{18}$ 其中 $f(Xbest_{_{i,j}}^t)$ 、 $f(Xbest_{_{i,j}}^t)$ 和 $f(X_{_{rr}}^t)$ 分别表示 $Xbest_{_{i,j}}^t$ 、 $X_{_{rl}}^t$ 和 $X_{_{rr}}^t$ 的适应度值。通过利用这种方法大大提升了白鲸搜索算法的局部搜索能力,进而提高了白鲸在高维空间中跳出局部最优的能力、搜索精度和收敛性能。

3.4 IBWO伪代码

对BWO的探索阶段进行了改进同时结合两种通用策略，提出了一种改进的群体教学优化算法（MGTOA）。通过上述改进策略，增强了MGTOA的探索能力与收敛速度，使计算更加全球化。

Initialization parameters T, Tmax, ub, lb, N, dim, Wk.
Initialize population X according to Equations (1).
Calculate the fitness value of all individuals, and select the optimal solution G
While T≤Tmax
Obtain balance factor Bf by Eq. (3) and probability of whale fall Wf by Eq. (10).
For i=1:N
If Bf (i) > 0.5
The beluga Exploration phase is achieved according to Formula (4).
Else If Bf (i) ≤ 0.5
The beluga Exploitation phase is achieved according to Formula (5-7).
End If
For i=1:N
If Bf (i) ≤ Wf
The beluga Whale fall is achieved according to Formula (8-10).
Determine whether the new location is within the boundary and calculate the fitness value based on its location
End If
End For
For i=1:N
Calculate with Dynamic pinhole imaging strategy Formula (13)
End For
For i=1:N
Calculate with Quadratic interpolation strategy Formula (14)
End For
End For
Find the current best solution G
T = T+1
End While
Output the best solution