文章目录
- 排序的概念
- 排序的概念:
- 排序运用
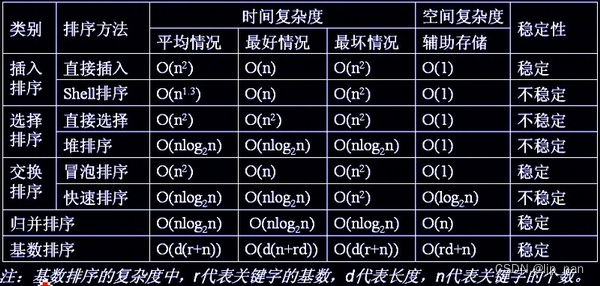
- 常见的排序与时间复杂度
- 插入排序
- 希尔排序
- 希尔排序的概念
- 希尔排序总结
- 选择排序
- 概念
排序的概念
排序的概念:
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
排序运用
1、当输入规模n比较小的时候,应该使用选择排序或者时插入排序(插入排序通常会比选择排序少一些比较的次数,但是选择排序会比插入排序少挪动的次数);
2、当输入的数据基本有序的时候,应该使用插入排序或者是随机的快速排序。
3、当n较大,要求速度较快的时候可以使用nlgn的算法比如:堆排序、快速排序和归并排序。堆排序的空间复杂度为lO(1)、而快速排序的空间复杂度是O(logn)(递归使用栈的情况),而归并排序的时间复杂度最大是O(nlogn).
常见的排序与时间复杂度
插入排序
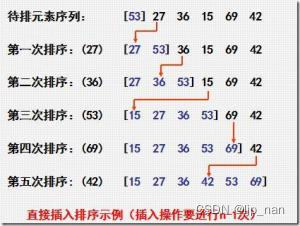
插入排序详解:插入排序就像我们在打扑克牌时摸牌的过程,在已有的有序数据中插入新的数据,使新的数据列有序。
插入排序的过程图:
实现代码:
void InsertSort(int* a, int n)
{
//多趟插入排序
for (int i = 0; i < n-1; i++)
{
//一趟插入排序
//在[0,end]区间内新增数据插入。
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
希尔排序
希尔排序的概念
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
如图示,gap从5,3,1的希尔排序。
希尔排序步骤:
1、进行预排序。
2、插入排序。
完整代码如下所示:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int j = 0; j < gap; j++)
{
for (int i = j; i < n - gap; i += gap)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
}
希尔排序总结
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就
会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些书中给出的时间复杂度不唯一:
总的来说希尔排序的时间复杂度为O(n^1.3)。
选择排序
概念
基本思想: 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
直接选择排序:
- 在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
- 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
- 在剩余的array[i]–array[n-2](array[i+1]–array[n-1])集合中,重复上述步骤,直到集合剩余1个元素

我们在这里书写提升版的选择排序,先选出最大的和最小的数,排升序把最小的数放在前面,最大的数放在后面。代码如下:
void SelectSort(int* a, int n)
{
int left = 0;
int right = n - 1;
while (left < right)
{
int min = left;
int max = left;
for (int i = left; i <= right; i++)
{
//选出最大的
if (a[max] < a[i])
{
max = i;
}
//选出最小的
if (a[min] > a[i])
{
min = i;
}
}
Swap(&a[min], &a[left]);
if (max == left)
{
max = min;
}
Swap(&a[max], &a[right]);
left++;
right--;
}
}
好的我们下一篇再见!