目录
Zilliz Cloud是什么?
为什么选择Zilliz Cloud?
基于Milvus构建,针对性能进行优化
弹性和可扩展
按需付费
多云支持(AWS、GCP)
云原生的可靠性
企业安全和治理
Zilliz Cloud基于Milvus的云原生服务
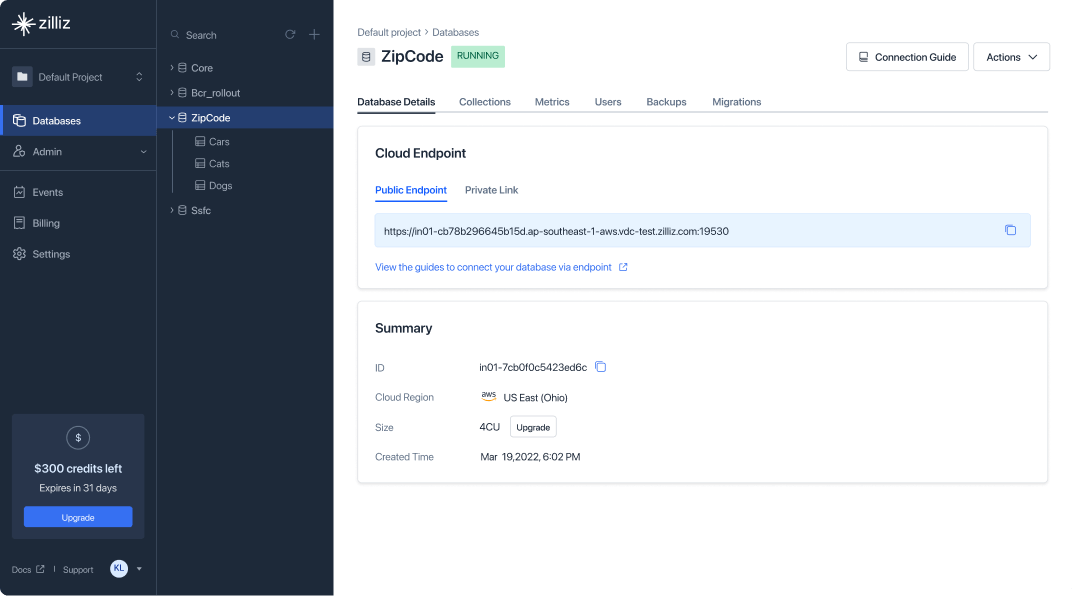
Zilliz简化了部署和扩展向量搜索应用程序的过程,无需创建和维护复杂的数据基础设施。
- 强大而灵活,支持多种机器学习算法生成的嵌入向量
- 对任何大小的数据集进行快速查询
- 高效存储向量的经济实惠方式
- 通过无服务器架构,零操作开销
Zilliz Cloud是什么?
Zilliz Cloud是一个完全托管的向量数据库,可以实现10倍更快的向量检索,这是其他任何向量数据库管理系统无法比拟的成就。
为什么选择Zilliz Cloud?
基于Milvus构建,针对性能进行优化
Zilliz Cloud基于流行的开源向量数据库Milvus构建。Milvus的创建者利用他们在各个行业的数千个企业Milvus用户上的经验,创建了最先进的向量数据库服务。
弹性和可扩展
通过即时创建和扩展与您的预算和需求相匹配的无服务器集群,以经济高效的方式进行扩展。将计算和存储资源扩展到支持数十亿个向量的程度。
按需付费
根据需要进行扩展或缩减,并仅支付所使用的费用,以降低存储嵌入向量的成本。新用户在前30天内可获得100美元的免费使用额度。通过承诺使用量获得高容量工作负载的按比例折扣。
多云支持(AWS、GCP)
Zilliz Cloud在所有云平台上提供一致的管理、安全性和治理体验。您无需为每个云平台重新投资创建过程,以支持您的数据和人工智能工作。相反,您的团队可以专注于利用所有数据来构建新的相似性搜索功能。
云原生的可靠性
Zilliz Cloud始终采用最新版本,在最新补丁的保护下安全,并得到全球一流的运维团队的支持。利用Milvus的可靠性和弹性构建,提供99.9%的正常运行时间SLA和零数据损坏。
企业安全和治理
Zilliz Cloud在传输过程中提供完整的数据加密,并符合SOC 2标准,将很快支持基于角色的访问控制(RBAC)。