补充说明：

1、决定性问题：

一个决定性问题(decision problem)是指其输出，只有“是”或“否”的问题。

一、P问题（polynomial time class）

1、问题描述：

可于确定型图灵机以多项式时间求解的决定性问题。
当一个决定性问题存在一个能在多项式时间内找出解的算法时，则称此问题落在P 的集合中。

2、典型问题：

质数问题、支撑树问题、匹配问题、拟阵问题、二拟阵交问题、网络流问题、中国邮路问题、最短路问题等均属P问题。

二、NP问题（NP，non-deterministic polynomial）

1、问题描述：

可在多项式时间内验证其解是否正确，但不保证能在多项式时间内能找出解的决定性问题。
当一个决定性问题的解能在多项式时间内被验证时，则称此问题落在NP 的集合中。
NP包含P和NP-complete问题, 因此NP集合中有简单的问题和不容易快速得到解的难题。

2、典型问题：

团问题(clique problem)、完全子图问题、图着色问题、旅行商(TSP)问题等等。
可满足性问题 (satisfiability problem，简称 SAT)，也是一个NP中的典型问题。

三、NP困难问题（NP-hardness, non-deterministic polynomial-time hardness）

如果所有NP问题都可以多项式时间归约到某个问题，则称该问题为NP困难。
因为NP困难问题未必可以在多项式时间内验证一个解的正确性（即不一定是NP问题），因此即使NP完全问题有多项式时间的解（P=NP），NP困难问题依然可能没有多项式时间的解。

四、NP完全问题（NP-C，NPC，NP-Complete）

1、问题描述

​
一个决定性问题C若是为NPC（NP完全），则代表它对NP是完全的，这表示：

• 它是一个NP问题
• 它是一个NP困难问题
• 其他属于NP的问题都可在多项式时间内归约（reduce to）成它。

2、典型问题：

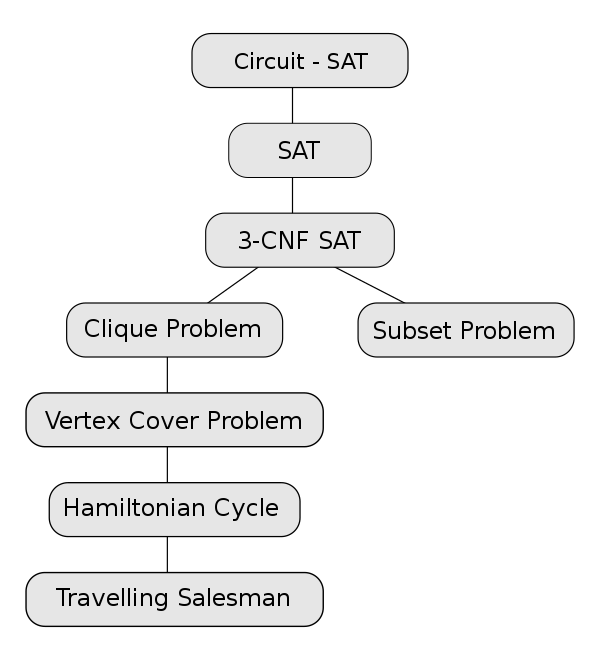
子集合加总问题
图同构（isomorphism）问题
布尔可满足性问题
N-puzzle问题（华容道问题）
背包问题
汉弥尔顿循环问题
旅行推销员问题
子图同构问题（Subgraph isomorphism problem）
子集合加总问题
分团问题
顶点覆盖问题（Vertex cover）
独立顶点集问题（Independent set problem）
图着色问题
扫雷