目录
- Visibility / Occlusion(可见性 or 遮挡)
- Painter's Algorithm(画家算法)
- Z-Buffer(深度缓冲算法)
- Shading(着色)
- A Simple Shading Model(Blinn-Phong Reflectance Model)一个简单的着色模型:Blinn-Phong反射模型
- Diffuse Reflection(漫反射)
- 参考资源
Visibility / Occlusion(可见性 or 遮挡)
延续上节课的内容,补充一下关于深度缓冲算法的知识。
Painter’s Algorithm(画家算法)
画画的时候,从后向前画;先画远的物体,近的物体会覆盖远的物体。
需要按照深度进行排序,假如有 n n n个三角形,时间复杂度就是 O ( n l o g n ) O(n log^{n}) O(nlogn)。
但是可能会出现无法按照深度顺序解决的情况:
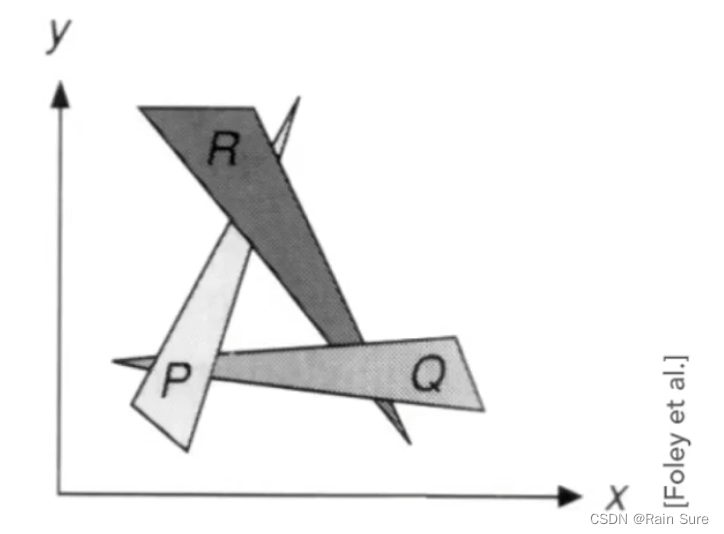
Z-Buffer(深度缓冲算法)
对于每个三角形按照深度排序可能会出现不太好处理的情况,但是对于每个像素可以记录一个深度最近的颜色。
思路:
- 对于每个像素,存储当前最小的深度值。
- 需要一个额外的缓冲来存储深度值:
- frame buffer stores color values 帧缓冲器存储颜色值
- depth buffer (z-buffer) stores depth 深度缓冲器来存储深度值
为了简化考虑,假设 z z z值永远是正值,越小的值表示越近,越大的值表示越近。
如下图所示,深度越近颜色越深;反之,颜色越浅。

初始的时候,深度缓存中记录的深度都是正无穷大。
算法流程:

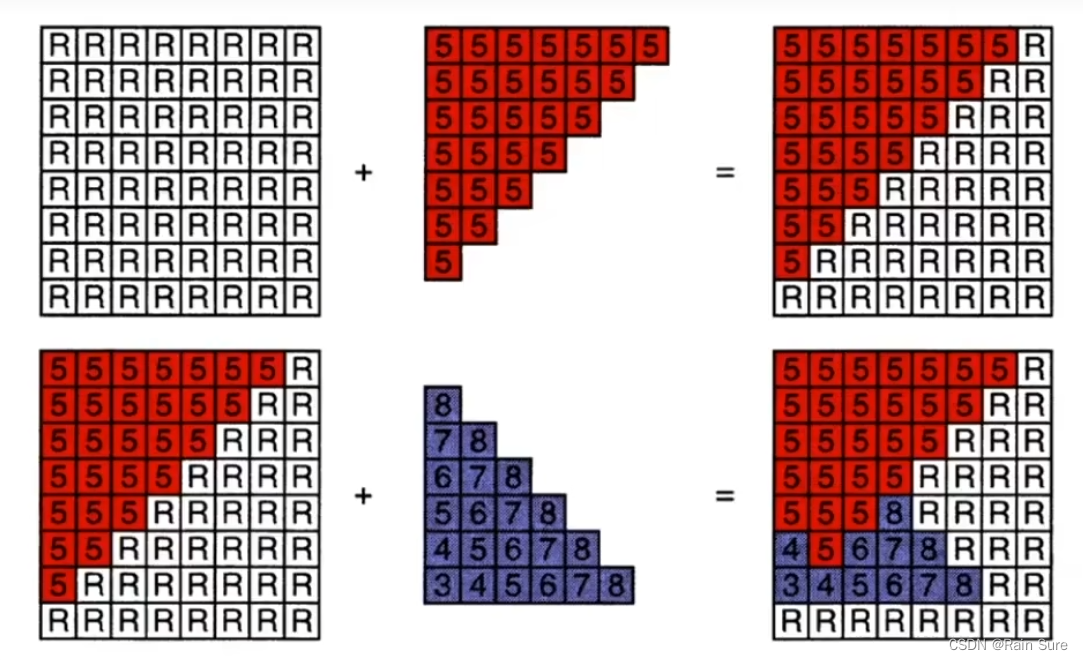
假设每个三角形都覆盖常数个像素,那么对于
n
n
n个三角形,时间复杂度就是
O
(
n
)
O(n)
O(n)。
Shading(着色)
着色就是对不同物体应用不同材质的过程。
A Simple Shading Model(Blinn-Phong Reflectance Model)一个简单的着色模型:Blinn-Phong反射模型
Blinn-Phong反射模型主要由三个部分组成:Specular highlights(高光部分), Diffuse reflection(漫反射), Ambient lighting(环境光)。

在开始之前,做如下定义:
考虑光照在任何一点上(shading point)的着色结果是什么,这个点可以在一个平面上,也可以在一个曲面上,
但是,我们认为在一个局部的极小的范围内,它一定在一个平面上。
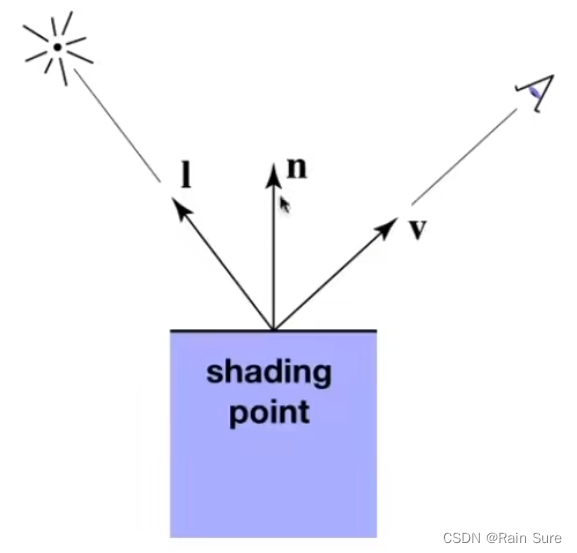
平面的法线:
n
⃗
\vec{n}
n
观测方向:
v
⃗
\vec{v}
v
光照方向:
l
⃗
\vec{l}
l
这些向量我们都只想表示方向,所以都是单位向量。
我们考虑任何一个点的着色,只考虑它自己,不考虑其它物体的存在。
没有阴影会产生!着色具有局部性!
Diffuse Reflection(漫反射)
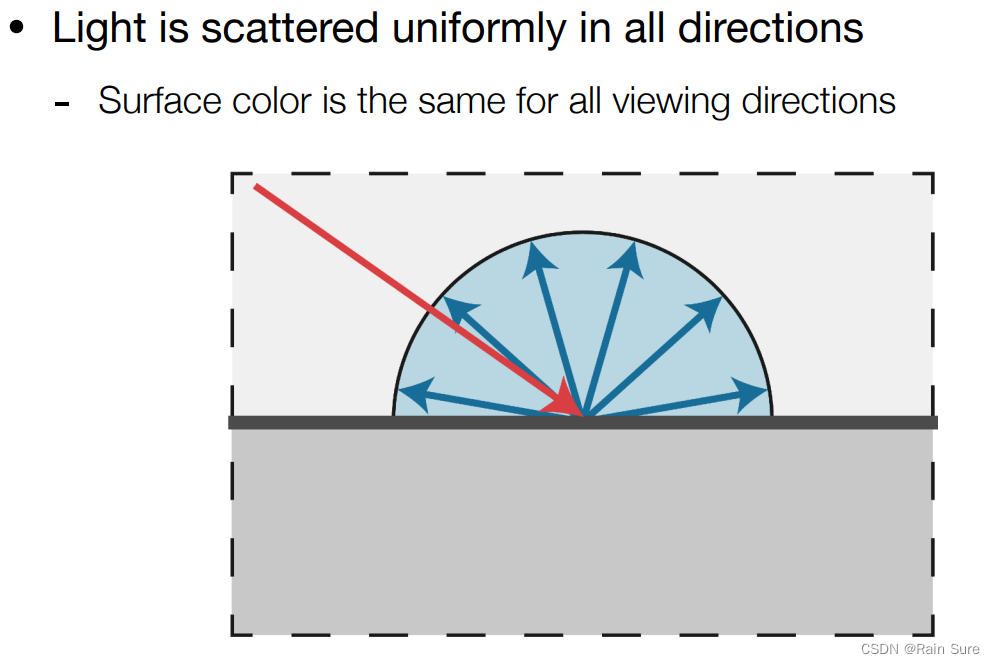
当有一根光线打到物体表面时,这根光线会被均匀地反射到各个方向去。
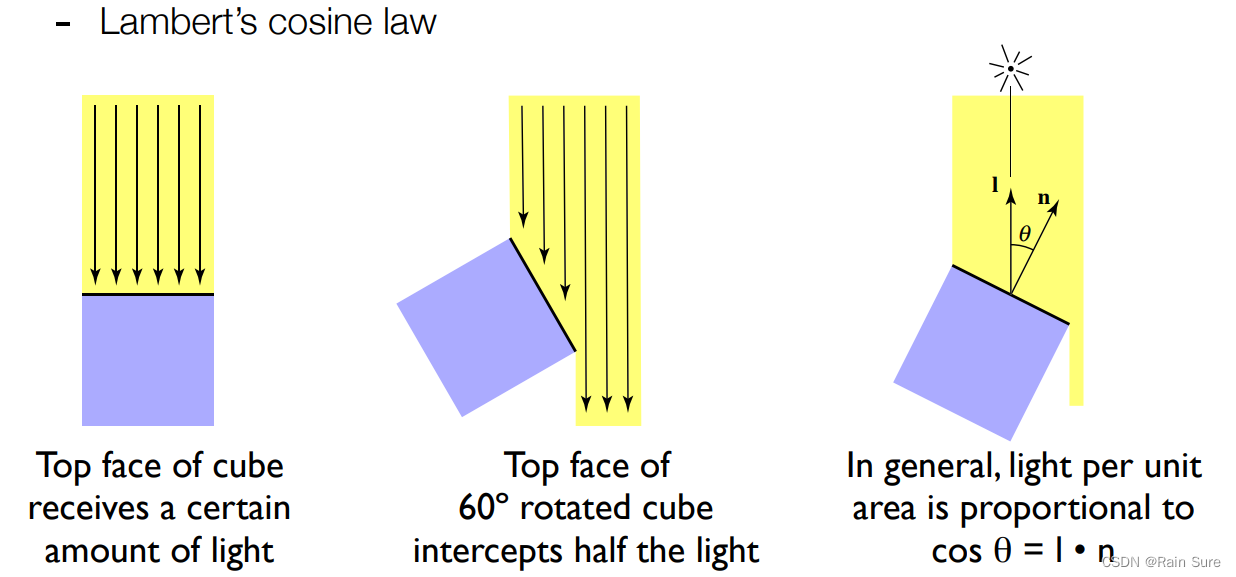
Lambert’s cosine law:
在单位面积上接收到的能量取决于光照强度和夹角(光照方向和法线方向的夹角)。
单位面积的能量和夹角的余弦值成正比。
我们认为一个点光源所传播的能量,在某一个时间一定是集中在一个球壳上。
并且,根据能量守恒定律,在任何一个球壳上的能量都相等。
因此,随着传播过程中,球壳越来越大,在单位面积上的能量越来越少。
单位面积的能量为:
I
/
r
2
I / r^2
I/r2
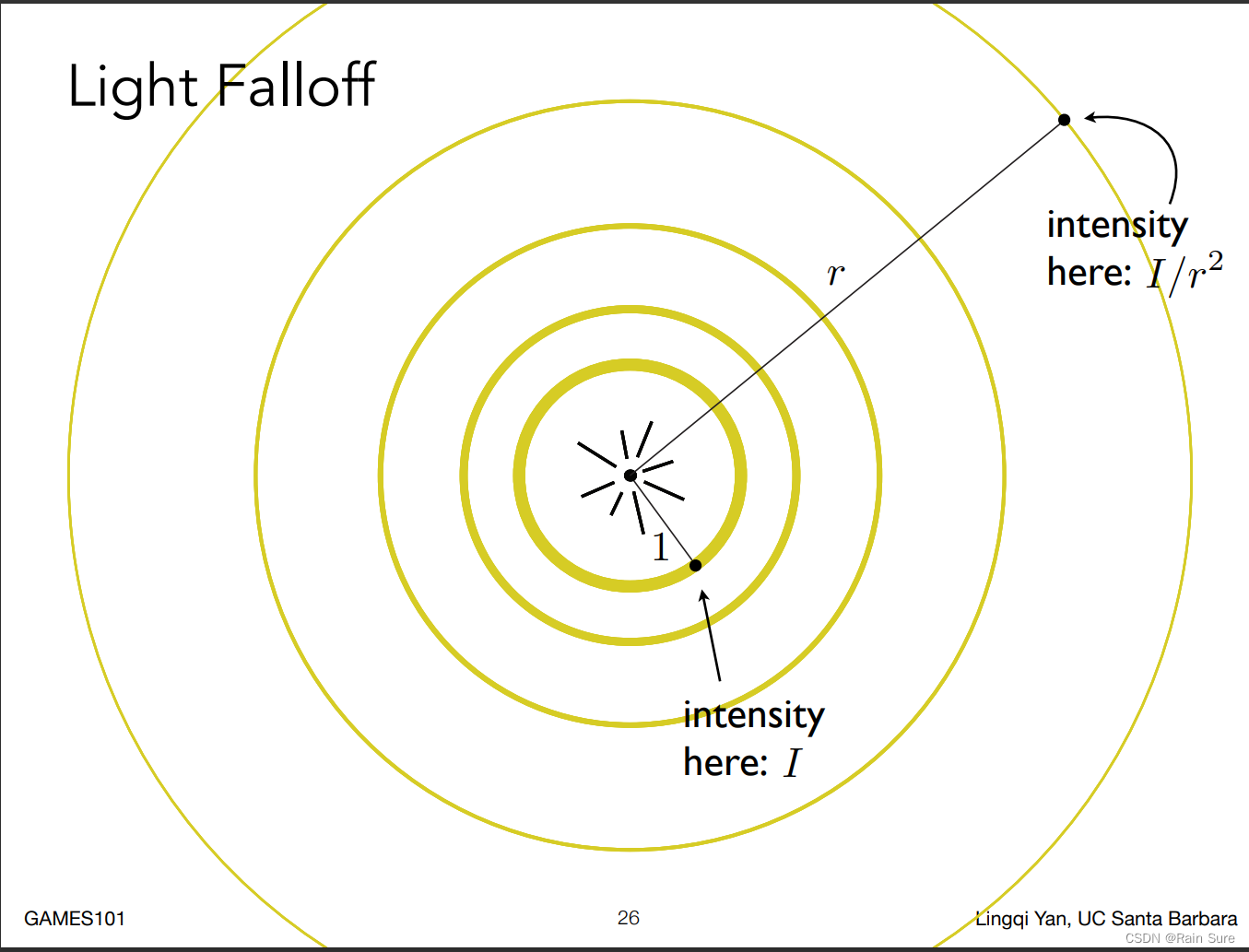
因此,我们可以得出漫反射应该看到的亮度的计算公式:
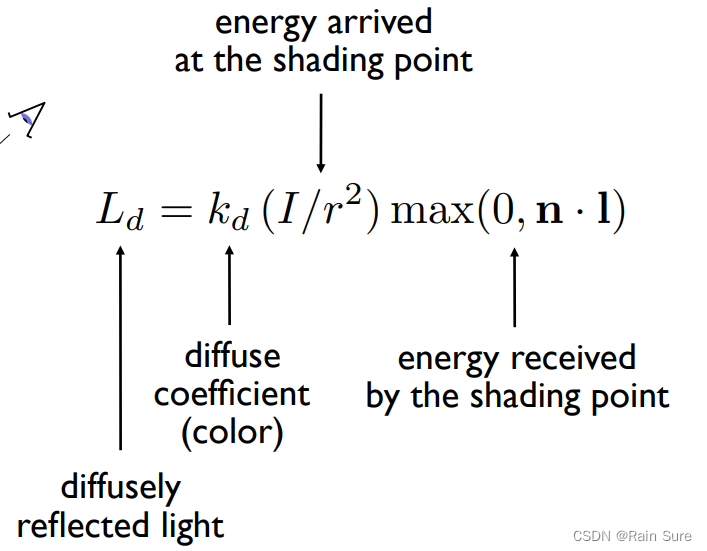
漫反射与观测角度完全没有关系,因为漫反射均匀地向四面八方反射。
参考资源
GAMES101 Lecture07