堆的向下调整算法

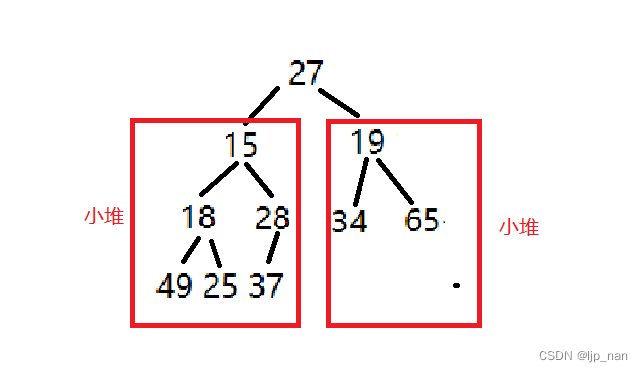
我们在这里都已小堆为例：

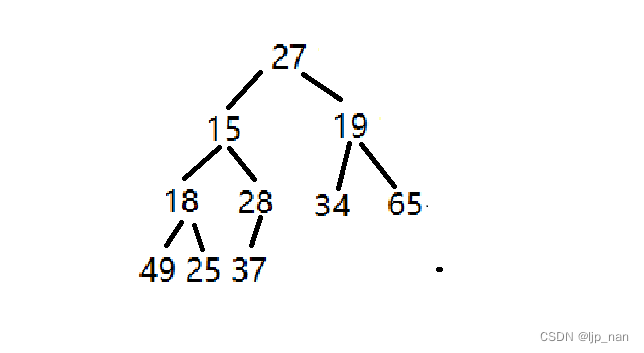
在这里我们有一个数组
int array[] = {27,15,19,18,28,34,65,49,25,37};
我们通过把根节点向下调整，使数组在逻辑上变成一个小堆。
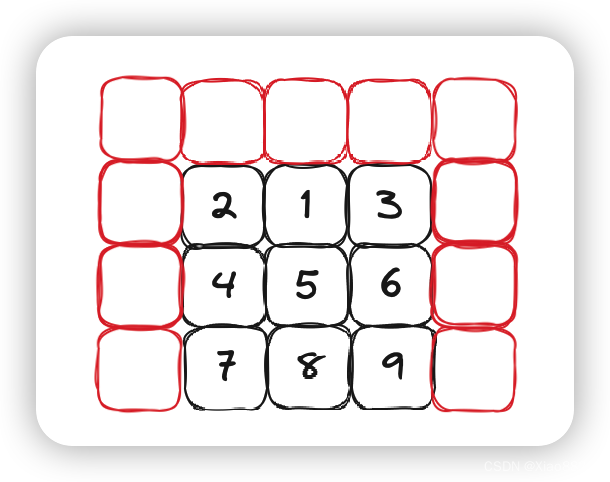
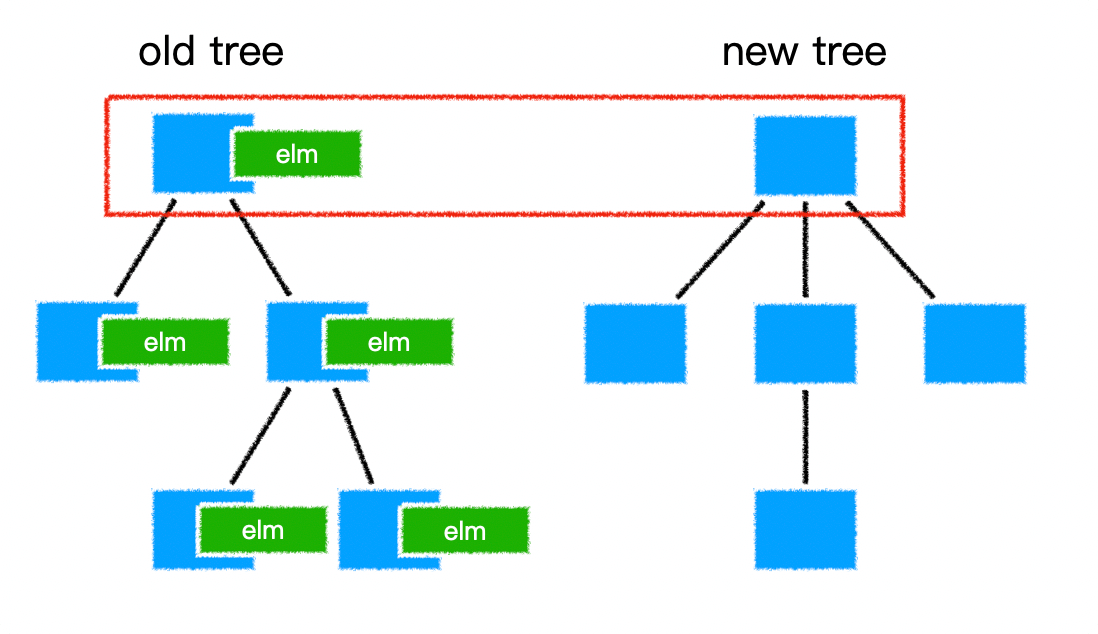
还未调整前的数组形成的完全二叉树：

注意向下调整有一个前提：根的左右子树是一个小堆，否则向下调整算法就没有意义了。

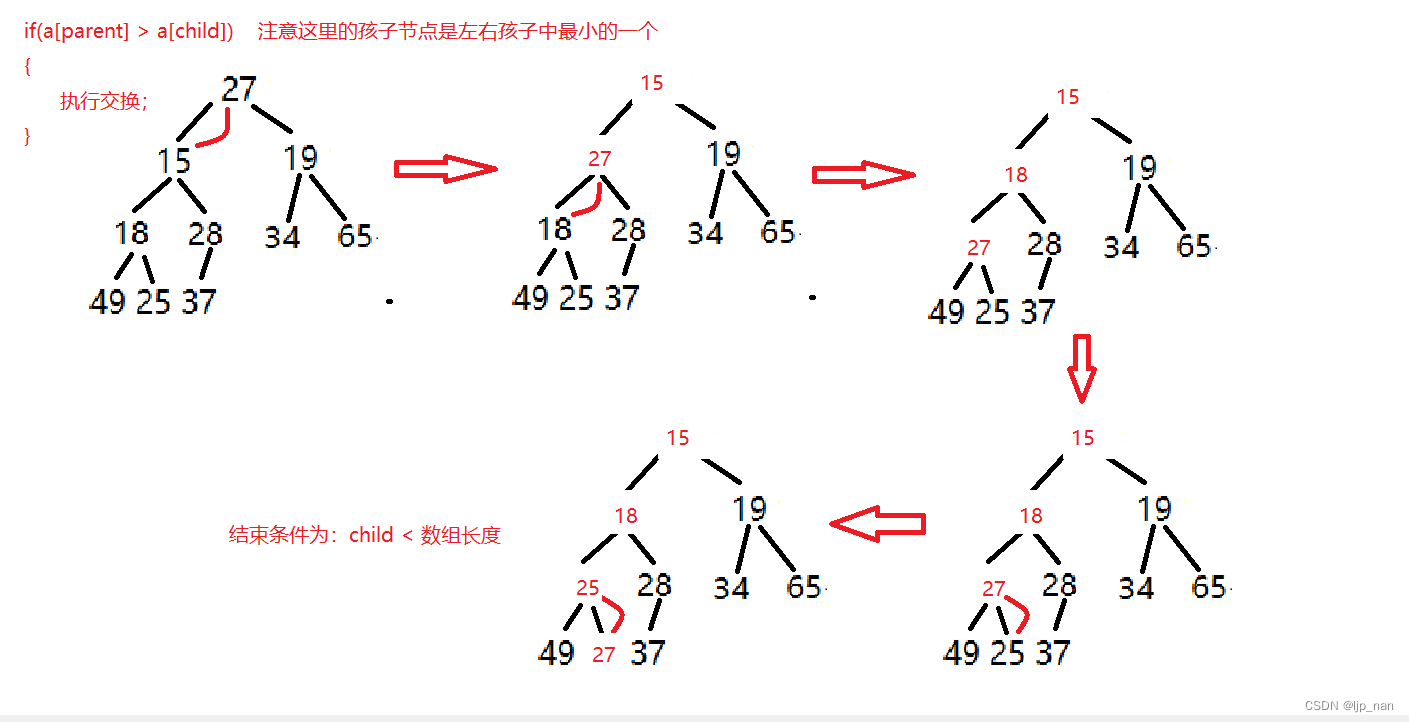
向下调整的过程：

具体的实现代码：

void AdjustDown(HPDataType* a, int n, int parent)
{
	assert(a);
	//建立小堆，我们假设左孩子是最小的
	int child = parent * 2 + 1; //算出左孩子的下标
	while (child < n) //这里判断条件是，孩子的下标大于等于size就停止循环
	{
		if (child+1<n&&a[child] > a[child + 1])  //child + 1 为右孩子，左孩子大于右孩子，那么右孩子是最小的
		{
			child++;
		}
		//程序走到这一步，就计算哪一个孩子是最小的了
		if (a[child] < a[parent])
		{
			//交换双亲和孩子节点
			Swap(&a[child], &a[parent]);
			//把孩子给双亲，再根据双亲算出下一层的孩子
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break; //调整的途中已经是一个小堆了，就break 意思就是 a[child] > a[parent] 相对于小堆。
			//没有左孩子一定没有右孩子，因为堆是一颗完全二叉树
		}
	}
}

堆的删除：

先把堆顶元素和最后一个元素交换，执行向下调整算法，把除了最后一个元素的数组调整为小堆。

void HeapPop(HP* php)
{
	assert(php);
	//堆为空时不能在进行删除
	assert(!HeapEmpty(php));
	//删除的思路
	//首先交换堆顶和堆底的数据，然后size--，执行向下调整的算法。
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	//执行向下调整算法
	AdjustDown(php->a, php->size, 0);
}

堆排序

思路：把一个数组利用向下调整算法调整为一个堆，先交换堆顶和最后一个元素。这样做的目的是将最小的交换到最后面。执行向下调整算法，把[0,end-1]区间内的元素向下调整为小堆，再重复以上步骤，就可以选出次小的，更小的。我们就完成了排序。
堆排序过程

结束条件为end > 0。
向下调整建堆时，要从第一个非叶子节点执行向下调整算法。
代码如下：

void HeapSort(HPDataType* a,int n)
{
	//首先执行向上调整算法把一个数组调整为堆
	/*for (int i = 1; i < n; i++)
	{
		AdjustUp(a, i);
	}*/
	//向下调整建堆
	//从第一个不是叶子节点的节点开始向下调整建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	//交换第一个和最后一个数据
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		//不把最后一个数据看成堆里面的数据,执行向下调整算法，选数据，再和最后一个数据交换
		AdjustDown(a, end, 0);
		end--;
	}
}
//时间复杂度为O(nlog(n))

向上调整建堆的时间复杂度

向上调整建堆是一个多乘多的问题。我们看如下的分析：

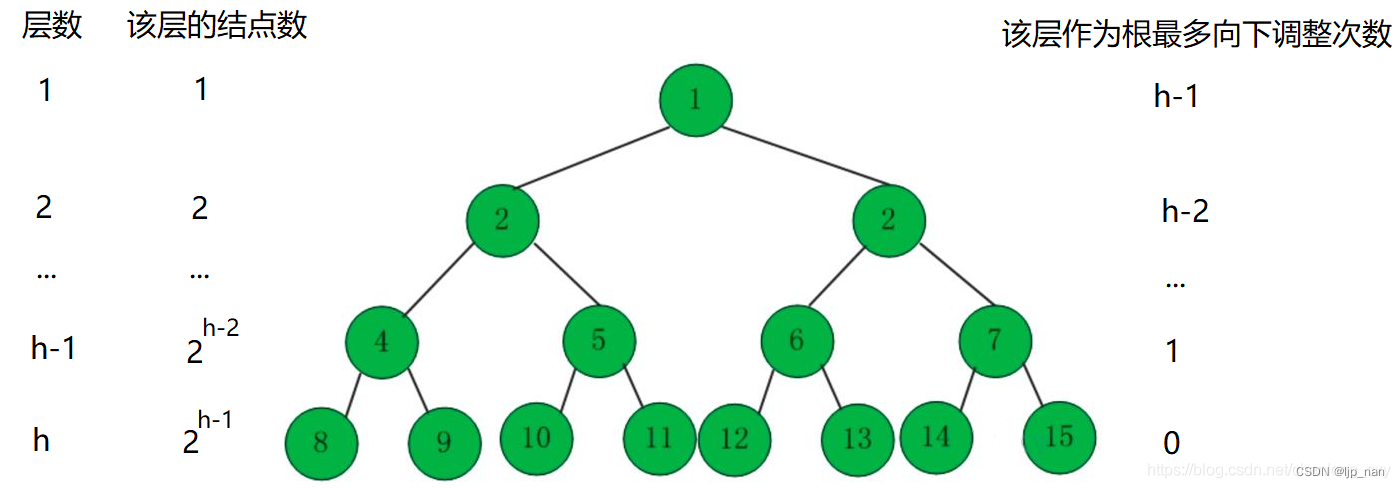
第一层：1个节点需要向上移动0次
第二层：2个节点需要向上移动1次
第三层：4个节点需要向上移动2次
第四层：8个节点需要向上移动3次
第 i 层： $2^(i-1)$ 个节点需要向上移动层数-1次
把上面的节点数和移动次数相乘，利用错位相减法可求得向上调整算法的时间复杂度为：
T(n)=O(logN)
建堆的时间复杂度为：O(nlogN)

向下调整建堆的时间复杂度为：

我们计算建堆过程中总共交换的次数：
在这里插入图片描述

TopK问题

概念：TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

思路：利用前k个数据建立小堆，用堆顶元素依次和剩余的n-k个数据比较，比堆顶元素小的就入堆。直至比较完毕，这样的算法大大节省了内存空间的开辟大小。
下面是代码：

void create()
{
	//生成随机数
	srand(time(0));
	int n = 10000;
	//把随机数生成到文件中
	FILE* pin = fopen("1.txt", "w");
	if (pin == NULL)
	{
		perror("fopen failed!\n");
		return;
	}
	//生成n个随机数写入文件中：
	for (int i = 0; i < n; i++)
	{
		int n = rand() % 100000;
		fprintf(pin, "%d\n", n);
	}
	fclose(pin);
}
void PrintTopK(int k)
{
	//打开文件
	FILE* pout = fopen("1.txt", "r");
	if (pout == NULL)
	{
		perror("fopen failed!\n");
		return;
	}
	//把前k个数据读入数组中
	int* arr = (int*)malloc(sizeof(int) * k);
	if (arr == NULL)
	{
		perror("malloc failed!\n");
		return;
	}
	for (int i = 0; i < k; i++)
	{
		fscanf(pout, "%d", &arr[i]);
	}
	//向下调整建立小堆
	for (int i = (k - 1 - 1) / 2; i > 0; i--)
	{
		AdjustDown(arr, k, i);
	}
	//再让剩余的n-k个数据和堆顶元素比较。
	//堆顶元素小于它让它进堆
	int val = 0;
	while (!feof(pout))
	{
		fscanf(pout, "%d", &val);
		if (arr[0] < val)
		{
			arr[0] = val;
			AdjustDown(arr, k, 0);
		}
	}
	//打印数据
	for (int i = 0; i < k; i++)
	{
		printf("%d ", arr[i]);
	}
}