机器学习复习7
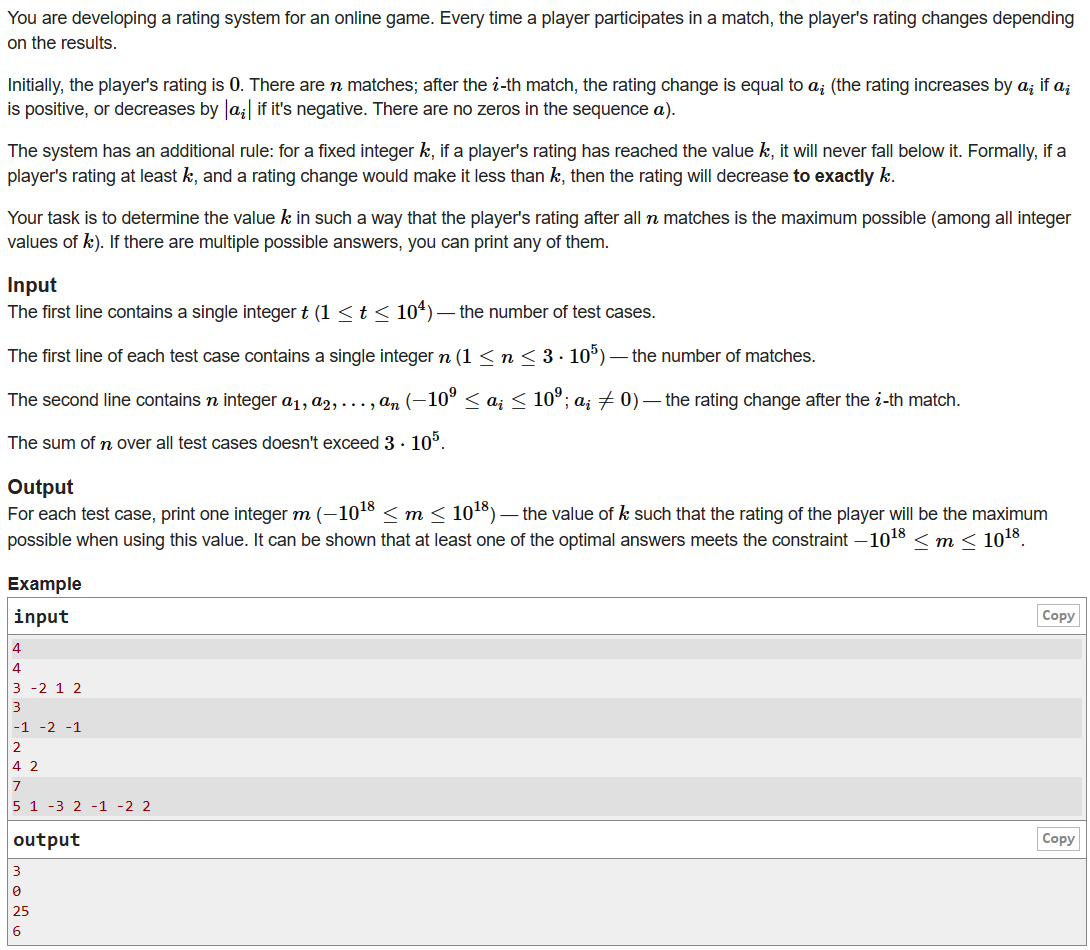
1 - 根据下图中绘制的决策树,如果一个动物的耳朵是软的,脸型是圆的,并且有胡须,那么这个模型会预测它是猫还是不是猫?
A. 不是猫
B. 是猫
**答案:B **
2 - 以一棵决策树学习来对垃圾邮件和非垃圾邮件进行分类。有20个训练实例,包括10个垃圾邮件和10个非垃圾邮件。
如果算法可以从四个特征中选择,产生四个相应的分割,它将选择哪一个(即纯度最高的)?
A. 左边分割:10封邮件中有5封是垃圾邮件。右边分割:10封邮件中有5封是垃圾邮件
B. 左边分割:2封邮件中有2封是垃圾邮件。右边分割:18封邮件中有8封是垃圾邮件
C. 左边分割:8封邮件中有7封是垃圾邮件。右边分割。12封邮件中有3封是垃圾邮件
D. 左边分割:10封邮件中有10封是垃圾邮件。右边分割:10封邮件中有0封是垃圾邮件
**答案:D **
3 - 熵的定义为 \(H(p_1) = - p_1 log_2(p_1) - p_0 log_2(p_0)\),其中 \(P_1\) 是正样本的占比,\(P_0\) 是负样本的占比
在一棵决策树的某一节点上,10个例子中有6个是猫,10个例子中有4个不是猫。哪个表达式可以计算熵 \(H(p_1)H(p_1)\) 这组10只动物的熵?

A. \((0.6) \log _{2}(0.6)+(1-0.4) \log _{2}(1-0.4)\)
B. -\((0.6) \log _{2}(0.6)-(1-0.4) \log _{2}(1-0.4)\)
C. \((0.6) \log _{2}(0.6)+(0.4) \log _{2}(0.4)\)
D. -\((0.6) \log _{2}(0.6)-(0.4) \log _{2}(0.4)\)
**答案:D **
4 - 信息增益
信息增益的定义:\(H\left(p_{1}^{\text {root }}\right)-\left(w^{\text {left }} H\left(p_{1}^{\text {left }}\right)+w^{\text {right }} H\left(p_{1}^{\text {right }}\right)\right)\)
在分裂之前,由5只猫和5只非猫组成的群体的熵是H(5/10) H(5/10)。在对某一特征进行分割后,由7只动物(其中4只是猫)组成的小组的熵为H(4/7)H(4/7)。另一组有3只动物(1只是猫),其熵为H(1/3)H(1/3)。信息增益的表达式是什么?
A. \(H(0.5)-\left(\frac{4}{7} * H(4 / 7)+\frac{4}{7} * H(1 / 3)\right)\)
B. \(H(0.5)-\left(\frac{7}{10} H(4 / 7)+\frac{3}{10} H(1 / 3)\right)\)
C. \(H(0.5)-(H(4 / 7)+H(1 / 3))\)
D. \(H(0.5)-(7 * H(4 / 7)+3 * H(1 / 3))\)
**答案:B **
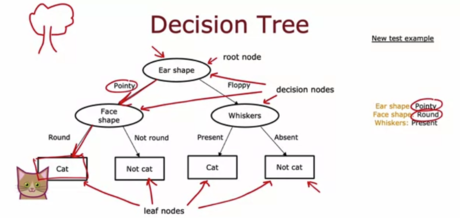
5 - 独热编码
为了表示耳朵形状的3种可能值,你可以为耳朵形状定义3个特征:尖耳朵、软耳朵、椭圆形耳朵。对于一个耳朵不尖、不软但呈椭圆形的动物,你如何用特征向量表示这一信息?
A. [0, 0, 1]
B. [1,0,0]
C. [0, 1, 0]
D. [1, 1, 0]
**答案:A **
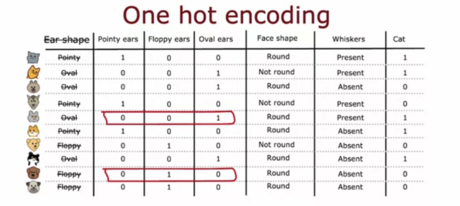
6 - 对于一个连续值的特征(如动物的体重),数据集中有10只动物。为该特征找到最佳分割的推荐方法是什么?
A. 选择10个例子之间的9个中点作为可能的分割点,并找到能带来最高信息增益的分割点
B. 尝试每一个间隔有规律的数值(例如,8、8.5、9、9.5、10等),并找到能带来最高信息增益的分割
C. 使用梯度下降法,找到能带来最高信息增益的分割阈值
D. 使用单次编码将特征转化为0和1的离散特征向量,然后应用我们讨论过的离散特征的算法
**答案:A **
7 - 其中哪些是决定停止分裂的常用标准?(多选)
A. 当树已经达到最大深度时
B. 当额外分裂的信息收益过大时
C. 当一个节点50%是一个类,50%是另一个类时(熵的最高值)
D. 当一个节点中的例子数量低于一个阈值时
**答案:AD **
8 - 对于随机森林,你如何建立每个单独的树,以使它们不都是彼此相同的?
A. 对训练数据进行无替换抽样
B. 在同一训练集上多次训练该算法。这自然会产生不同的树
C. 对训练数据进行替换采样
D. 如果你要训练B个树,就在训练集的1/B上训练每个树,所以每个树都是在一个不同的例子集上训练
**答案:C **
9 - 在一项分类任务中,你要在决策树和神经网络之间做出选择,输入x是一张100x100分辨率的图像。你会选择哪个?
A. 决策树,因为输入是非结构化的,决策树通常在非结构化数据中工作得更好
B. 一个神经网络,因为输入的是非结构化的数据,而神经网络通常对非结构化的数据工作得更好
C. 神经网络,因为输入的是结构化数据,而神经网络通常在结构化数据中工作得更好
D. 决策树,因为输入的是结构化数据,而决策树通常在结构化数据中工作得更好
**答案:C **
10 - 替代抽样指的是什么?
A. 它指的是使用一个新的数据样本,我们用它来永久地覆盖(也就是替换)原始数据
B. 它指的是对训练集做一个相同的拷贝的过程
C. 绘制一个例子的序列,当挑选下一个例子时,首先从我们要挑选的集合中删除所有以前绘制的例子
D. 绘制一个例子序列,当挑选下一个例子时,首先将所有先前绘制的例子从我们正在挑选的集合中替换掉
**答案:D **