1、题目

给定一个数 $N$，想象只由 0 和 1 两种字符组成的所欲长度为 $N$ 的字符串。

如果某个字符串，任何 0 字符的左边都有 1 紧挨着，认为这个字符串达标。

返回有多少达标的字符串。

2、思路

前几项推导：

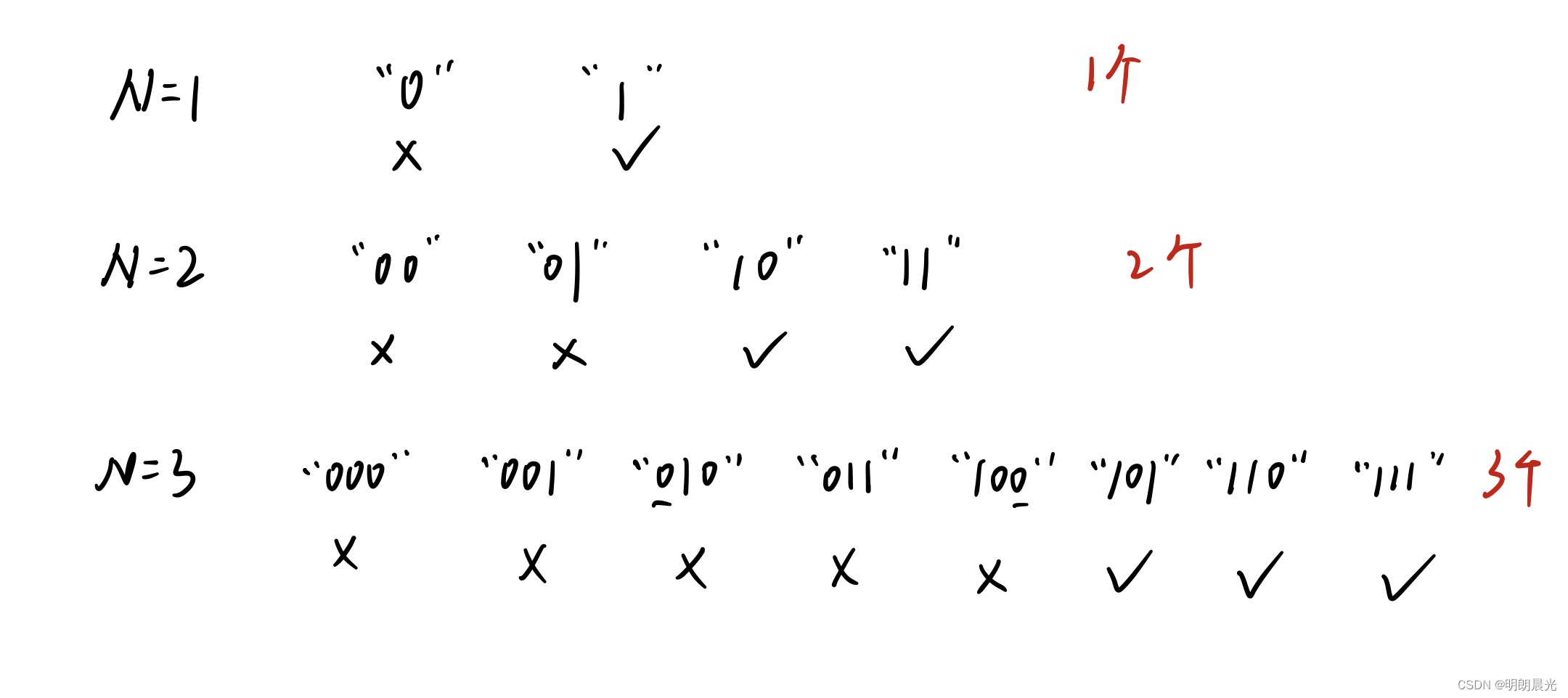
两种解法：

1、观察法：$1,2,3,5,8,13$ 的斐波那契数列

2、尝试法：

定义一个函数 int f(int i)，$f(i)$ 的含义是还有 $i$ 个格子需要填（填 0 或 1），但是有个潜台词——这 $i$ 个格子的前一个位置一定是 1 的情况下有多少个达标的。

如果 $N=6$，则函数调用的是 $f(5)$，因为第 1 个格子一定是 1，剩下的 5 个格子需要填。

在已经确定了 $i$ 个格子的前一个位置是 1 的情况下，有多少种填法：

• 1）$i$ 个格子的第一个位置填 1，则满足了 $f(i-1)$ 达标的条件
• 2）$i$ 个格子的第一个位置填 0，则第二个位置一定要填 1 才可能达标，此时满足了 $f(i-2)$ 达标的条件

所以：$f(i)=f(i-1)+f(i-2)$

public class Code03_ZeroLeftOneStringNumber {
	//方法一：递归
	public static int getNum1(int n) {
		if (n < 1) {
			return 0;
		}
		return process(1, n);
	}

	public static int process(int i, int n) {
		if (i == n - 1) {
			return 2;
		}
		if (i == n) {
			return 1;
		}
        //第 i个格子填1 + 第 i 个格子填0，则i+1一定填1
		return process(i + 1, n) + process(i + 2, n);
	}
	
	//方法2：递归
	public static int getNum2(int n) {
		if (n < 1) {
			return 0;
		}
		if (n == 1) {
			return 1;
		}
		int pre = 1;
		int cur = 1;
		int tmp = 0;
		for (int i = 2; i < n + 1; i++) {
			tmp = cur;
			cur += pre;
			pre = tmp;
		}
		return cur;
	}
	
	//方法3：矩阵乘法
	public static int getNum3(int n) {
		if (n < 1) {
			return 0;
		}
		if (n == 1 || n == 2) {
			return n;
		}
		int[][] base = { { 1, 1 }, { 1, 0 } };
		int[][] res = matrixPower(base, n - 2);
		return 2 * res[0][0] + res[1][0];
	}
	
	public static int[][] matrixPower(int[][] m, int p) {
		int[][] res = new int[m.length][m[0].length];
		for (int i = 0; i < res.length; i++) {
			res[i][i] = 1;
		}
		int[][] tmp = m;
		for (; p != 0; p >>= 1) {
			if ((p & 1) != 0) {
				res = product(res, tmp);
			}
			tmp = product(tmp, tmp);
		}
		return res;
	}

	// 两个矩阵乘完之后的结果返回
	public static int[][] product(int[][] a, int[][] b) {
		int n = a.length;
		int m = b[0].length;
		int k = a[0].length; // a的列数同时也是b的行数
		int[][] ans = new int[n][m];
		for(int i = 0 ; i < n; i++) {
			for(int j = 0 ; j < m;j++) {
				for(int c = 0; c < k; c++) {
					ans[i][j] += a[i][c] * b[c][j];
				}
			}
		}
		return ans;
	}

	public static void main(String[] args) {
		for (int i = 0; i != 20; i++) {
			System.out.println(getNum1(i));
			System.out.println(getNum2(i));
			System.out.println(getNum3(i));
			System.out.println("===================");
		}
	}
}