目录

一、平衡树 119

1.1 2-3查找树 119

1.1.1 2-结点和3-结点的含义 119 

1.1.2查找 120

1.2 2-3查找树的插入 121

1.2.1 向2-结点中插入新建 121

1.2.2向一棵树只含有一个3-结点的树中插入新建 121

1.2.3向一个父结点为2-结点的3-结点中插入新建 121 

1.2.4向一个父结点为3-结点的3-结点中插入新建 121

1.2.5分解根结点 121

1.3 2-3树的性质 122

1.4 2-3查找树的实现 122

二、红黑树 123

2.1红黑树的定义 123

2.2红黑树结点类API设计 124  

2.3平衡化 125

2.3.1左旋 

2.3.2左旋 

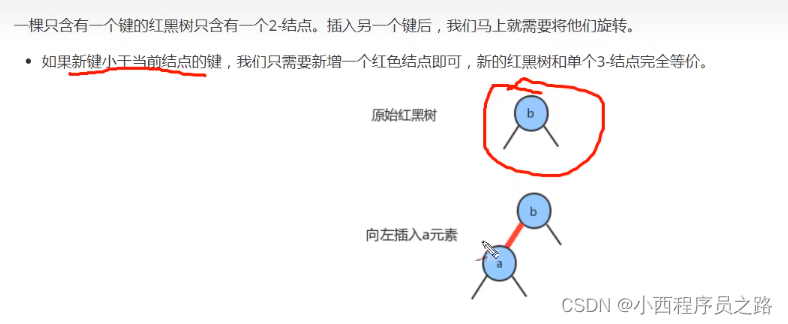
2.4向单个2-结点中插入新建 126

2.5向底部的2-结点插入新键 126

2.6颜色反转 126

2.7向一棵双键树（即一个3-结点）中插入新键 127

2.8根结点的颜色总是黑色 127

2.9向树底部的3-结点插入新键 127

2.10红黑树的代码实现 128

三、B-树 131

3.1B树的特性 131

3.2B树存储数据 132

2.3B树在磁盘文件中的应用 133

2.3.1磁盘 133

2.3.2磁盘IO 133

四、B+树 134

4.1B+树存储数据 134

4.2B树和B+树的对比 134

4.3B+树在数据库中的应用 135

---

一、平衡树 119

问题描述：结点9的查询效率比较高，但是查询结点1的时候，查询效率就会很低。

原因：结点1的深度太深了。 

解决问题方法：采取2-3查找树来解决树的不平衡问题。

1.1 2-3查找树 119

1.1.1 2-结点和3-结点的含义 119 

什么叫2-3查找树呢？

原因是：这种类型的查找树有两类，一种是2-结点和另外一种3-结点。

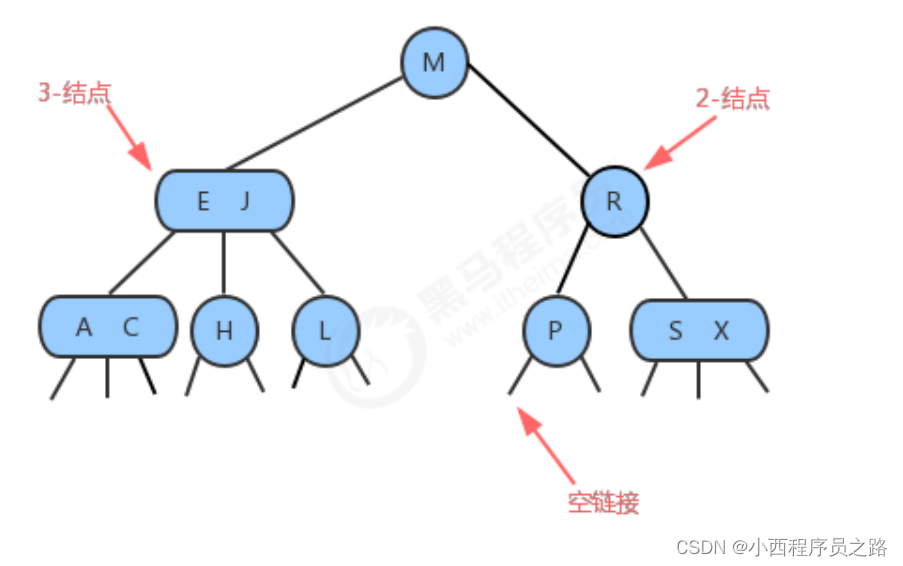
1.1.2查找 120

1.2 2-3查找树的插入 121

1.2.1 向2-结点中插入新建 121

步骤一：

根据二叉树的插入方法，先进行查找。如果查找到合适的位置。比如本案例如下，插入K。结果这个Z是在原来L结点的左子树上。

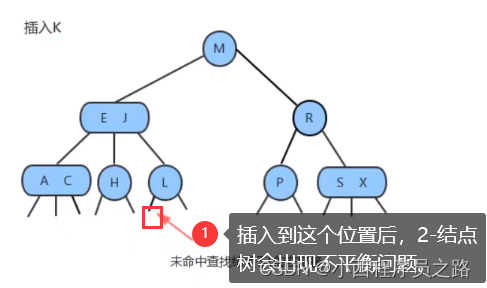
步骤二：

如果将K插入到L结点的左子树上，那么这个2-结点查找树就会被破坏平衡，所以采取将2-结点树变为3-结点树。

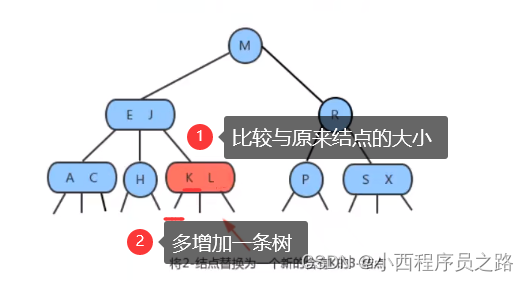
步骤三：和原来的结点进行比较，K小于结点L，所以需要放在L结点的左侧。如下图所示：

1.2.2向一棵树只含有一个3-结点的树中插入新建 121

1.2.3向一个父结点为2-结点的3-结点中插入新建 121 

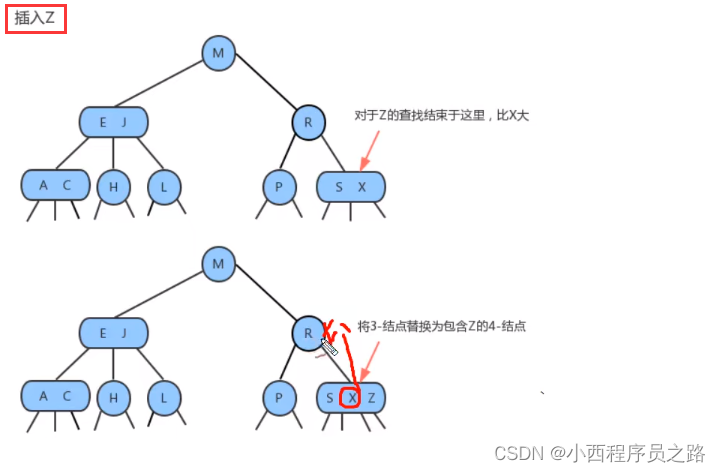
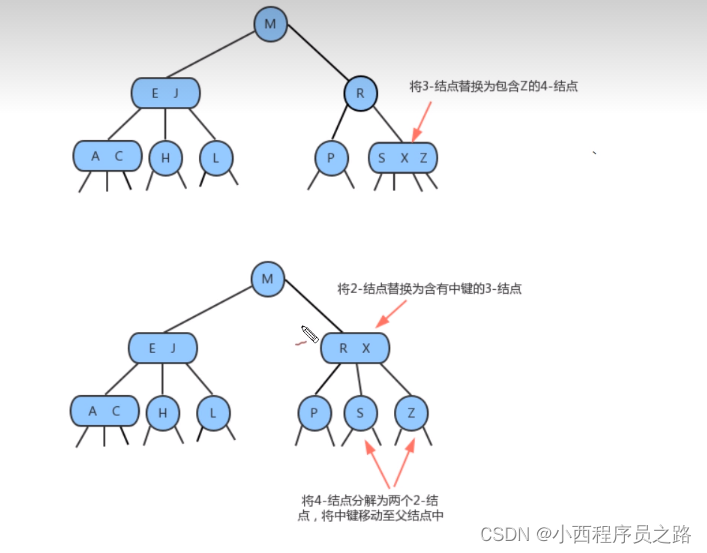
1.2.4向一个父结点为3-结点的3-结点中插入新建 121

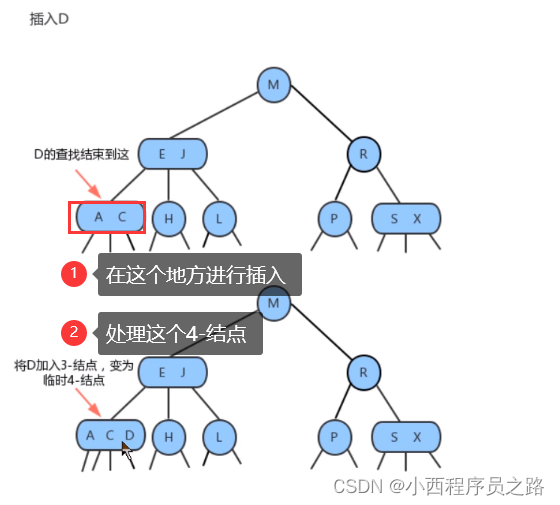
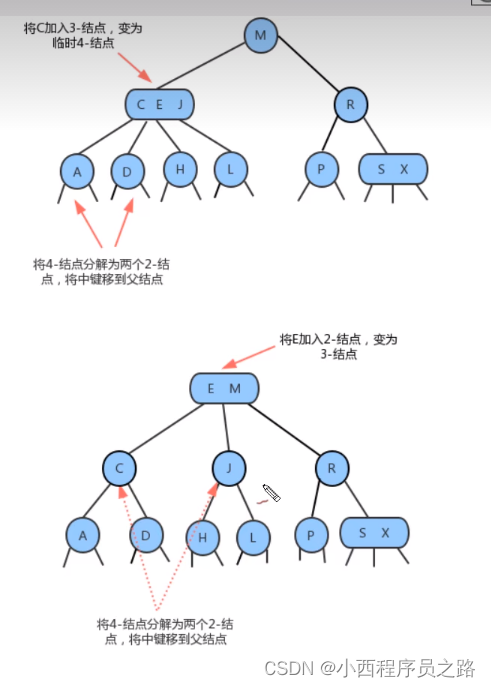
1.2.5分解根结点 121

 

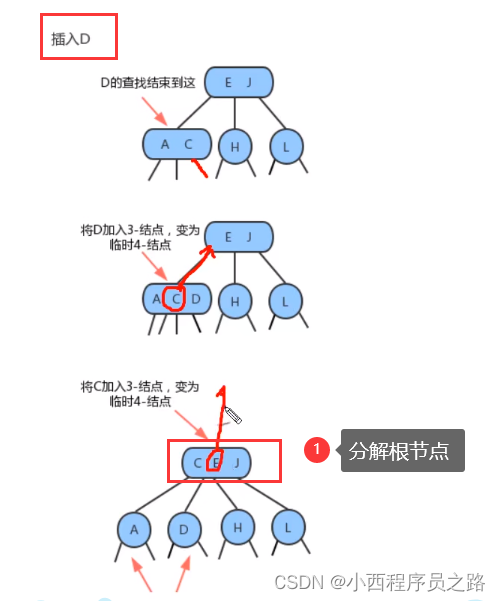
1.3 2-3树的性质 122

解释：

1、参考下面的这个树，A、D、H、L结点下面有这八个都是空链接（叶子）。其到根节点E的路径长度都一样长。

2、参考1.2.4向一个父结点为3-结点的3-结点中插入新建。

3、也可以参考1.2.4。和普通二叉树的最大区别，也是为什么是2-3查找树是平衡树的原因。

1.4 2-3查找树的实现 122

二、红黑树 123

2.1红黑树的定义 123

红黑树是基于2-3查找树实现的。

注：

1、利用2-结点和一些额外的信息（就是标注链接的颜色）来表示2-3查找树。

2、红黑树的红色链接只能左斜，不能右斜。

链接：红链接和黑链接 

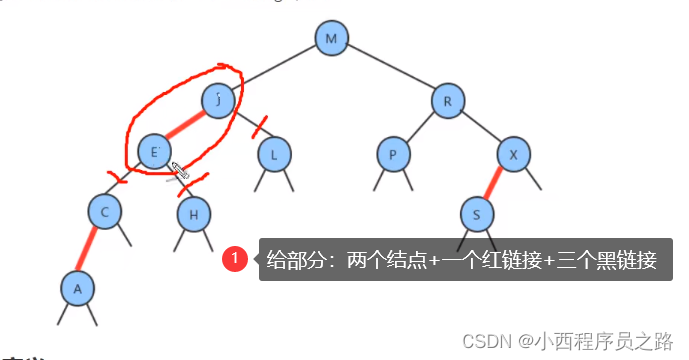
红黑树定义：

 注：

对定义3进行解释：之前1-3中的性质1：空连接到根节点的距离是相同的。

 红黑树和2-3树的对应关系：

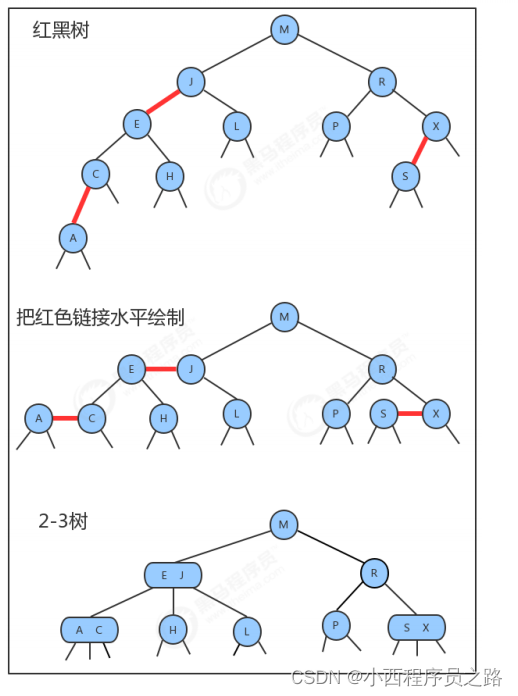
2.2红黑树结点类API设计 124  

 

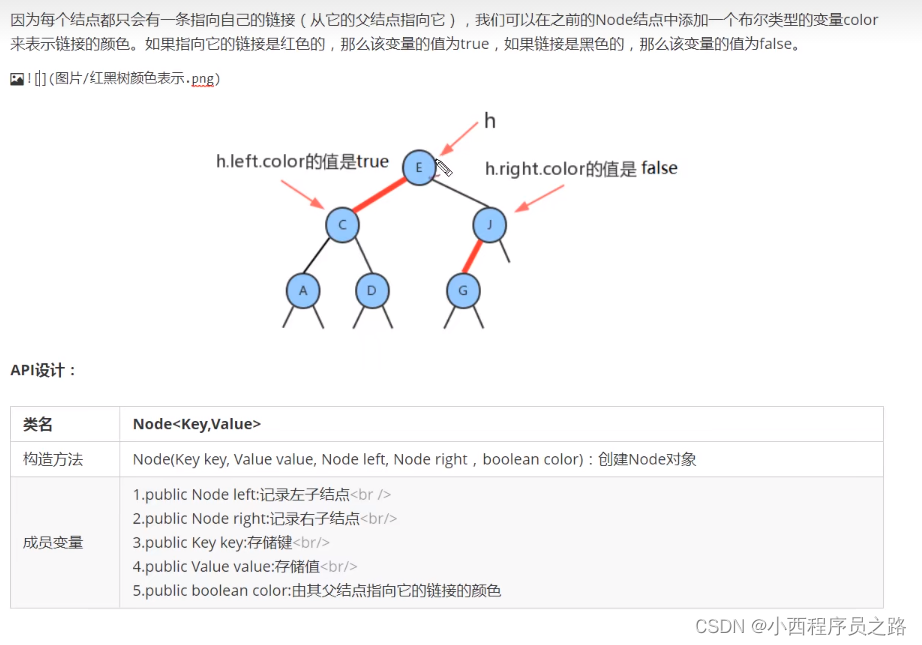
2.3平衡化 125

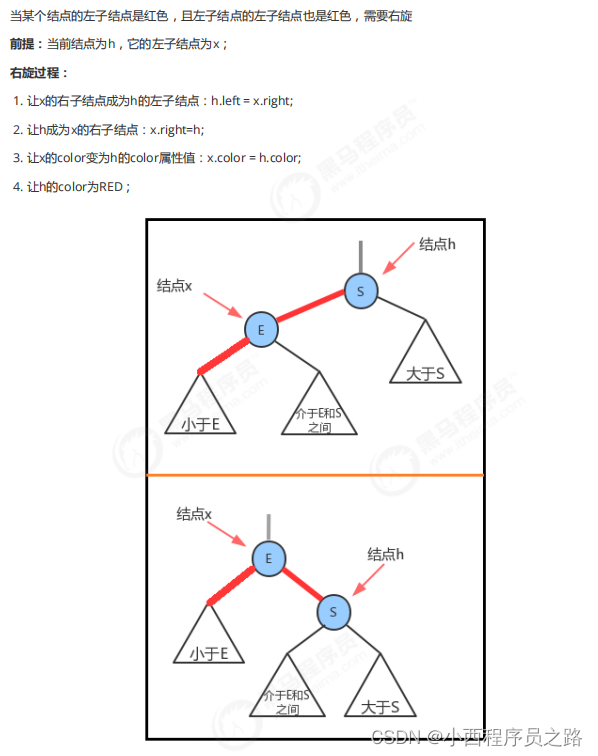
问题描述：如果进行对红黑树进行增删改查的操作后，会打破红黑树原有的平衡

解决方法：通过旋转进行修复，使得红黑树保持平衡

2.3.1左旋 

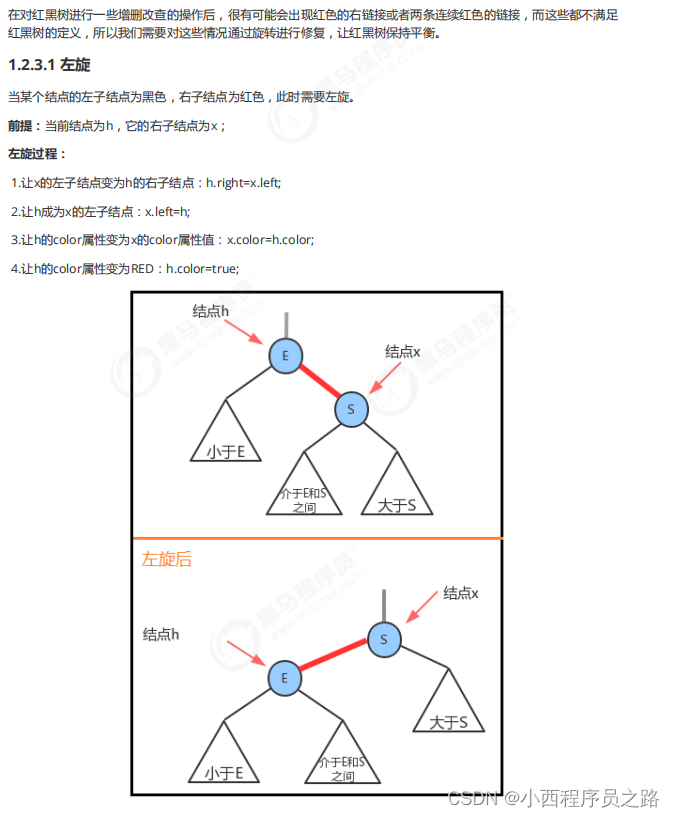
2.3.2左旋 

2.4向单个2-结点中插入新建 126

 

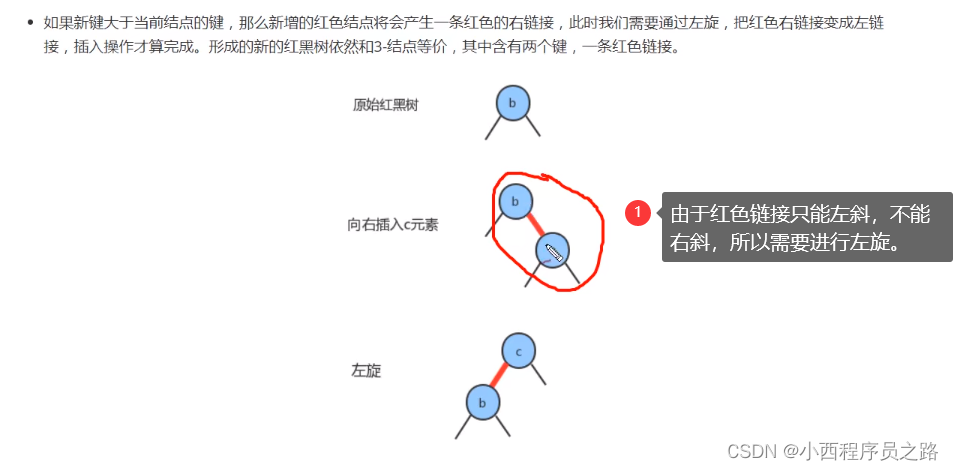
2.5向底部的2-结点插入新键 126

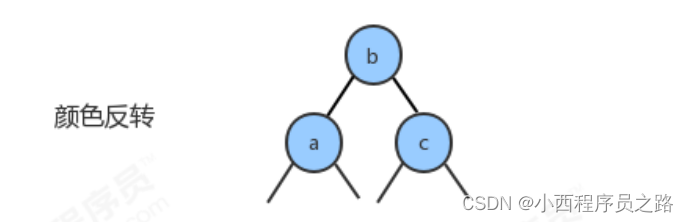
2.6颜色反转 126

解决办法：不能右侧存在红色链接，需要进行颜色反转，红色链接变为黑色，当前结点的链接变为红色。 

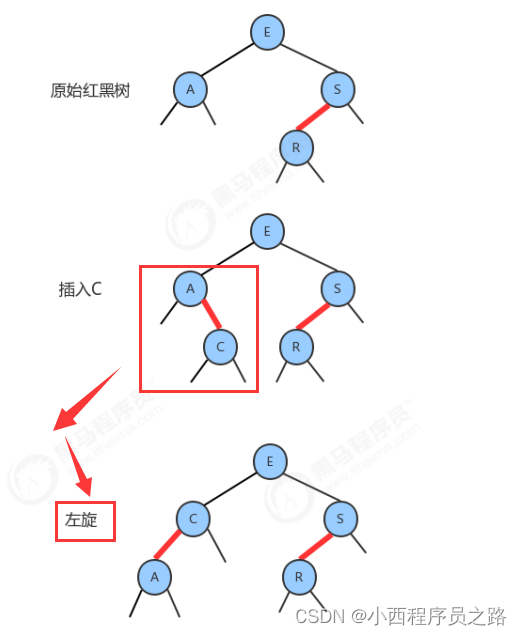
2.7向一棵双键树（即一个3-结点）中插入新键 127

 

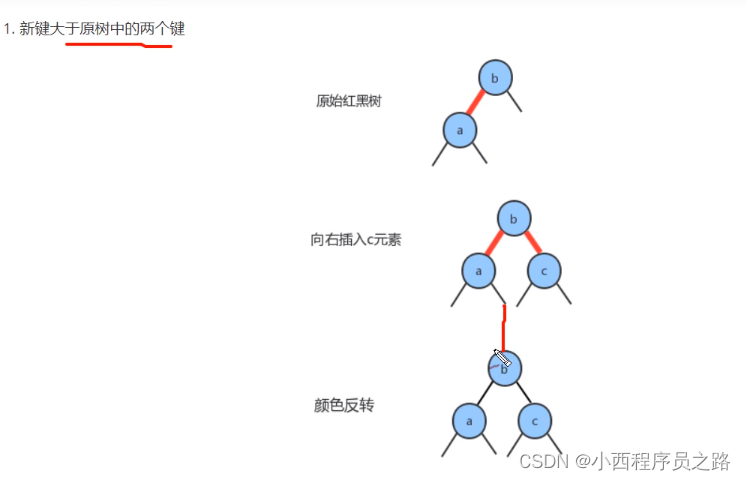
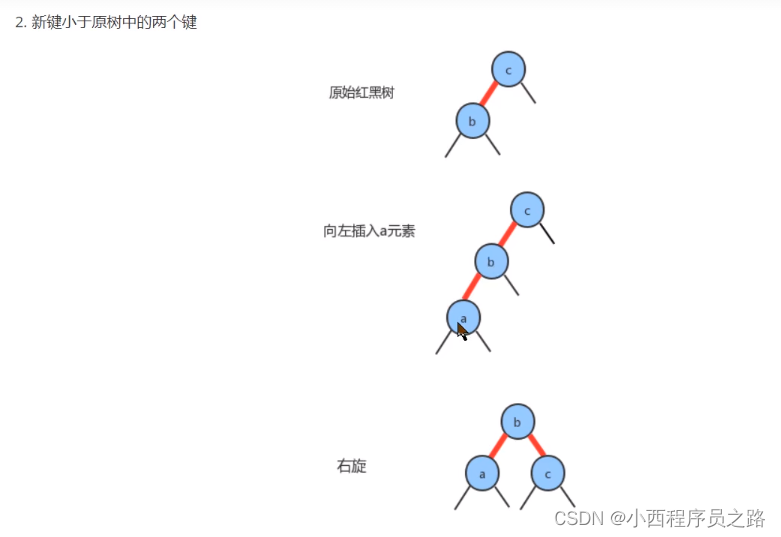
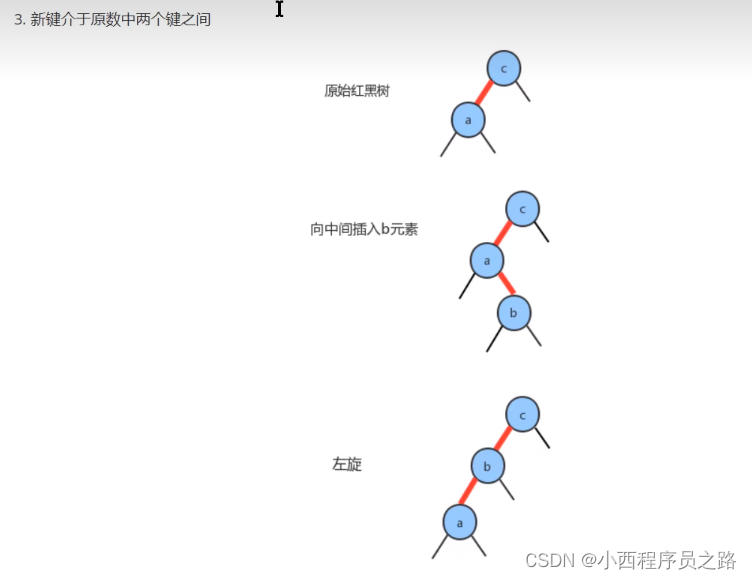
注：不能同时都是左斜的，需要进行右旋 

 

 

 

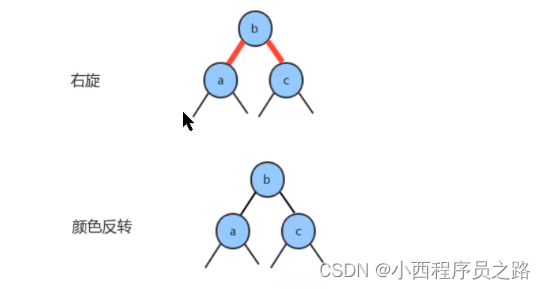
2.8根结点的颜色总是黑色 127

根结点的颜色总是黑色的。平衡化后的结果，根结点链接总是黑色的。

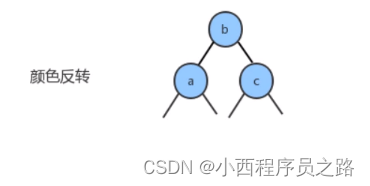
2.9向树底部的3-结点插入新键 127

本部分看文档原理P23。

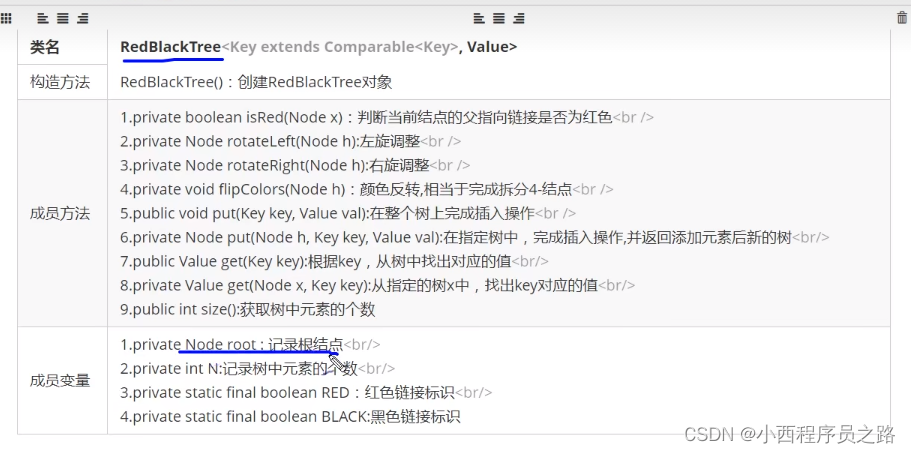
2.10红黑树的代码实现 128

本部分的代码实现在/tree/RedBlackTree中

左旋方法的实现：

 

 右旋方法的实现：

 颜色反转方法的实现：

 在整个树上完成插入操作：

 

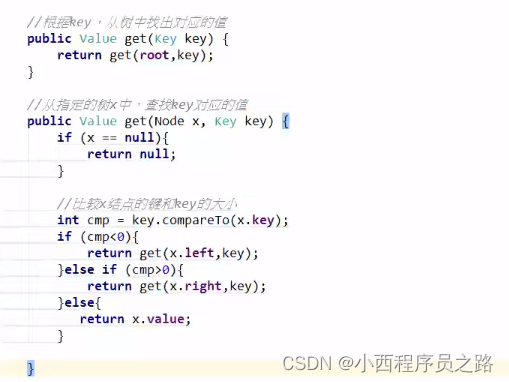
根据key，从树中找到对应的值方法： 

三、B-树 131

3.1B树的特性 131

 

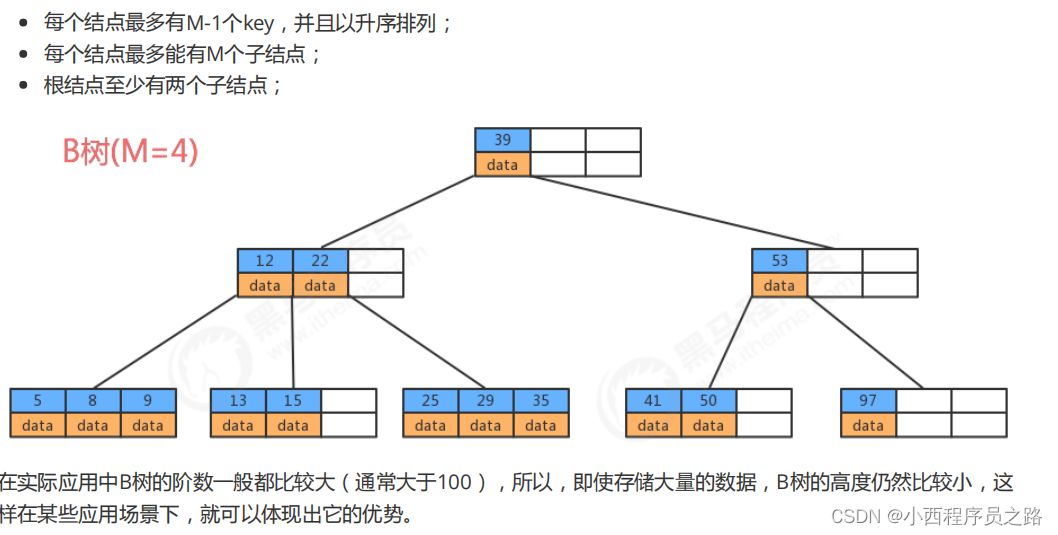
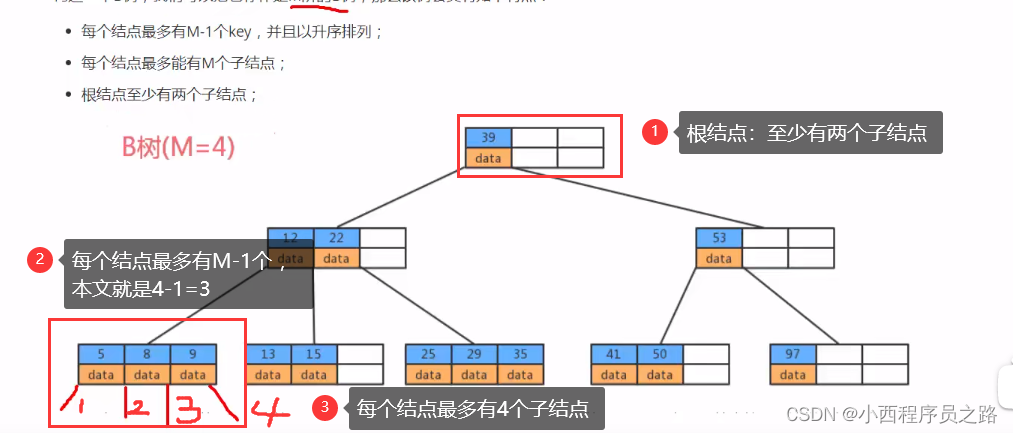
3.2B树存储数据 132

 

 

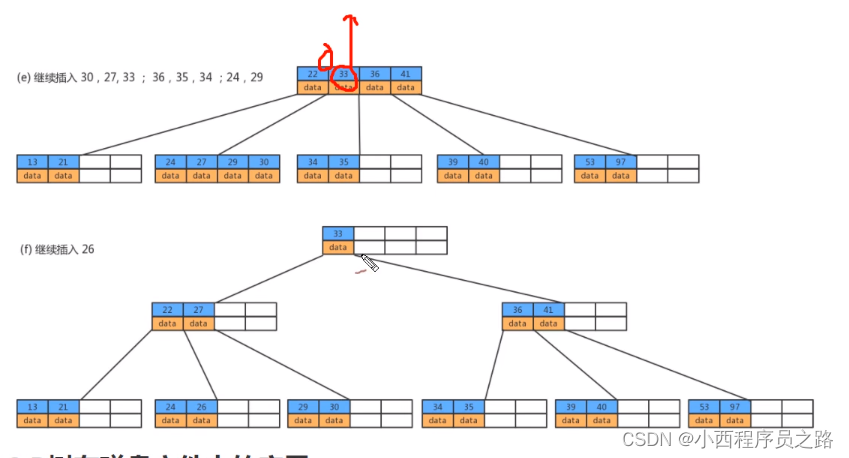
2.3B树在磁盘文件中的应用 133

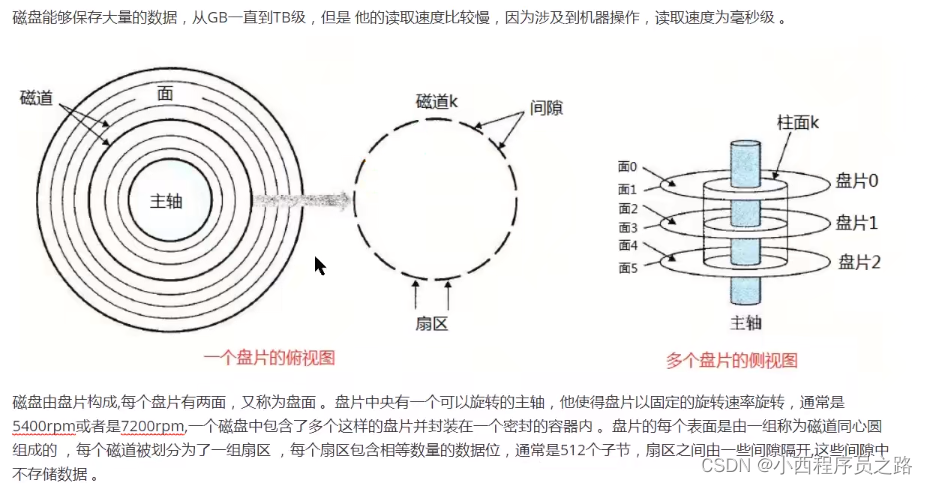
2.3.1磁盘 133

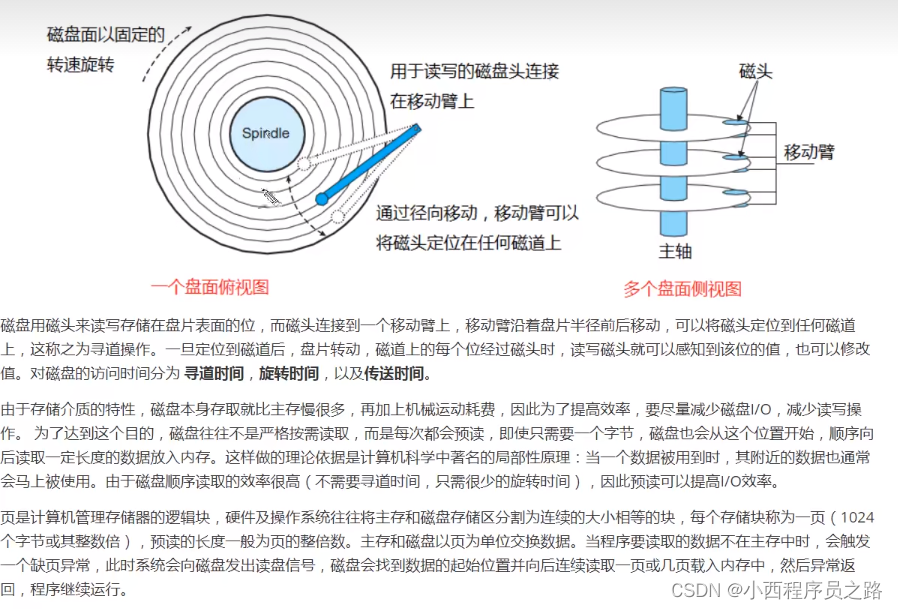
2.3.2磁盘IO 133

 

注：

1、如果将数据存在内存当中，就会减少磁头寻找磁道的时间。

2、缺页异常：表示利用B树进行保存

3、主要是提升从磁盘上读取数据的一个效率

四、B+树 134

 

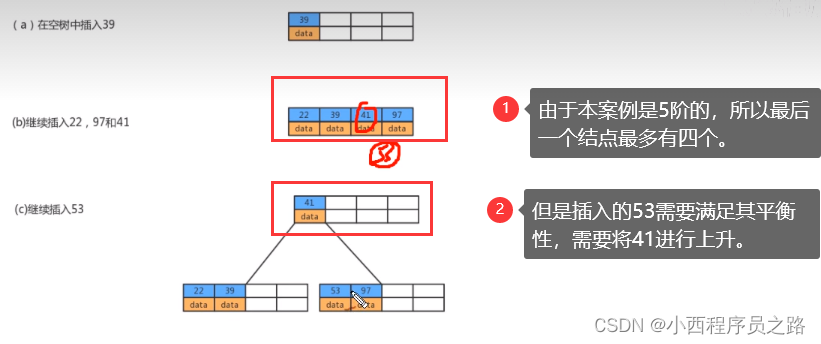
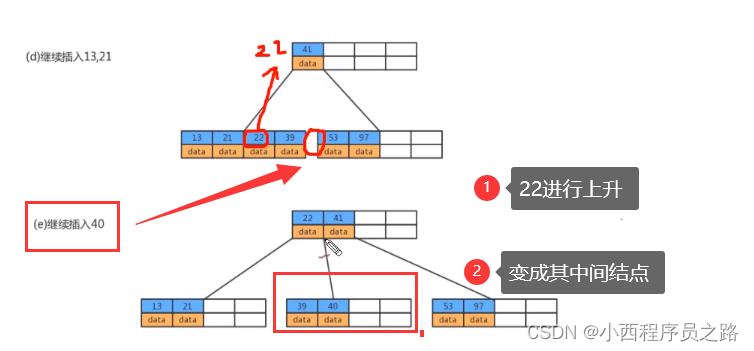
4.1B+树存储数据 134

B+树会自动的形成一个链表，插入过程的形成原理示意图如下所示：过程中也是用到B树自下向上的生长过程。

 

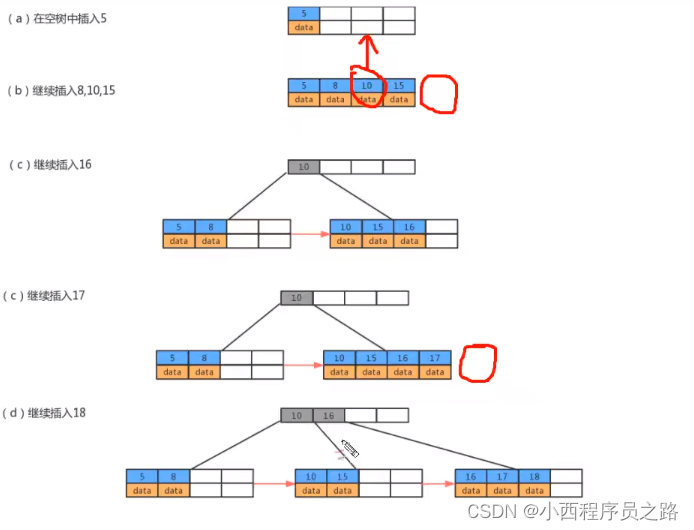
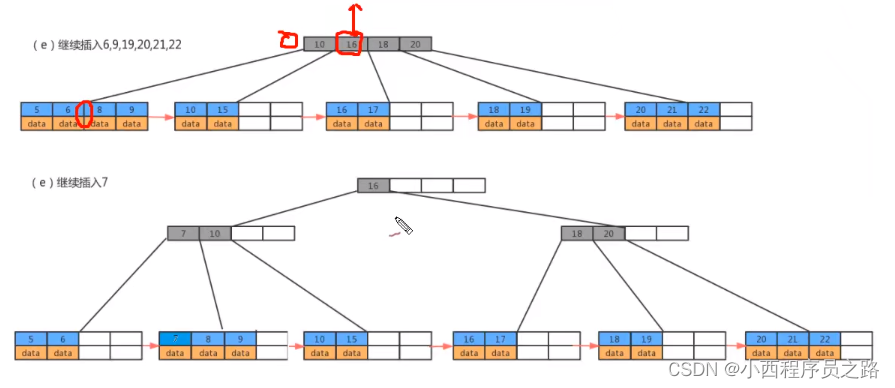
注：B+树实际上也是自下向上的生长。

4.2B树和B+树的对比 134

 

1、只存k 不存value，因此相比与B树，能够存更多的数据。

2、B+树遍历方便

4.3B+树在数据库中的应用 135

本部分看文档P35