【Spark大作业】财政收入影响因素分析及预测模型

news2024/11/17 23:36:31

文章目录

  • 前言
  • 一、数据的基本描述性分析
    • 1.1 导包与读取数据
    • 1.2 数据的基本情况
    • 1.3 变量的分布情况
    • 1.4 相关性分析
  • 二、数据的预处理
    • 2.1 Lasso变量选择模型
  • 三、建立财政收入预测模型
    • 3.1 灰色模型
    • 3.2 神经网络预测模型
  • 环境搭建
  • Spark pandsAPI接口（了解）
  • 分布式 + Spark进行数据处理
    • 文件上传hdfs（分布存储）
    • Spark数据处理

前言

1、对搜集的某市地方财政收入以及各类别收入数据，分析识别影响地方财政收入的关键属性
2、预测筛选出的关键影响因素的2014年、2015年的预测值。
3、评估模型的准确率。

参考资料：【数据挖掘案例】财政收入影响因素分析及预测模型

单机、小数据、pandas

一、数据的基本描述性分析

1.1 导包与读取数据

  • 数据(data.xlsx)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from pylab import mpl
import openpyxl

# 正常显示中文标签
mpl.rcParams['font.sans-serif'] = ['SimHei']
# 正常显示负号
mpl.rcParams['axes.unicode_minus'] = False
# 禁用科学计数法
pd.set_option('display.float_format', lambda x: '%.2f' % x)

# 读入数据
data = pd.read_excel('./input/data.xlsx')

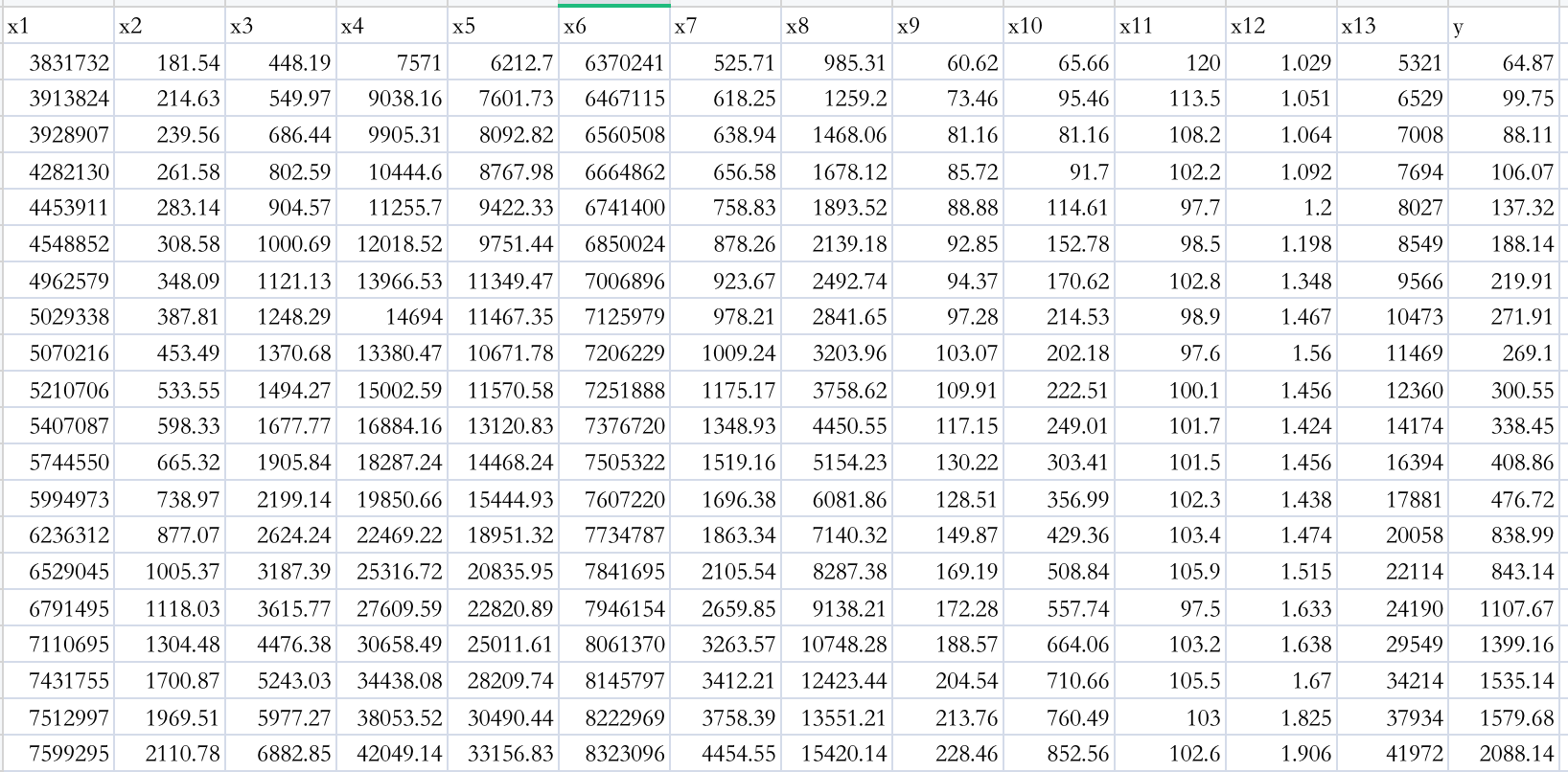
在这里插入图片描述

  • 字段含义
    • 社会从业人数(x1 )
    • 在岗职工工资总额（x2）
    • 社会消费品零售总额(x3)
    • 城镇居民人均可支配收人(x4)
    • 城镇居民人均消费性支出(x5)
    • 年末总人口(x6)
    • 全社会固定资产投资额(x7)
    • 地区生产总值（x8）
    • 第一产业产值（x9）
    • 税收（x10）
    • 居民消费价格指数（x11）
    • 第三产业与第二产业产值比（x12）
    • 地区生产总值(x8)和居民消费水平(x13)

1.2 数据的基本情况

data.shape # (20, 14)
data.info()

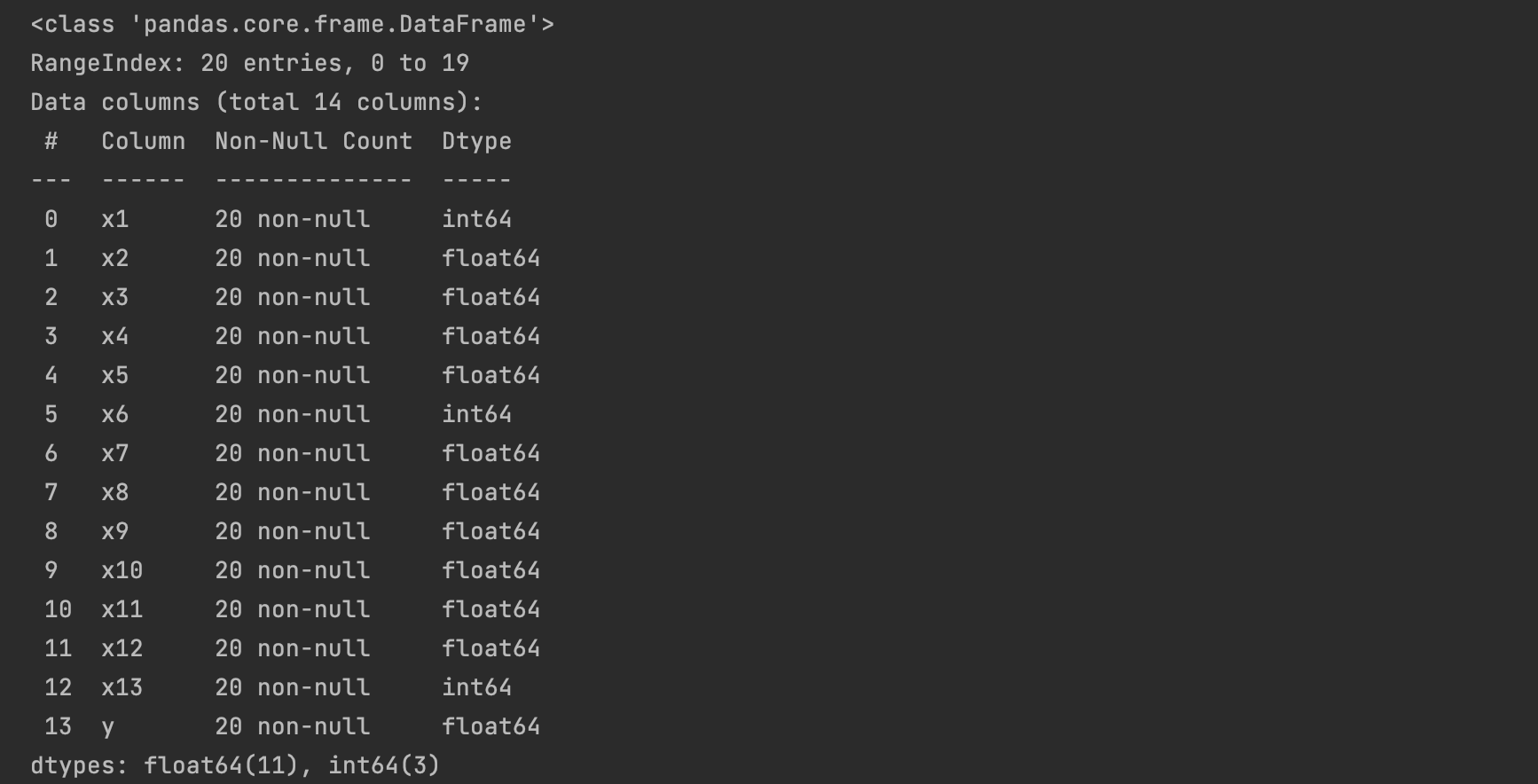
在这里插入图片描述

# 描述性分析
data.describe().T

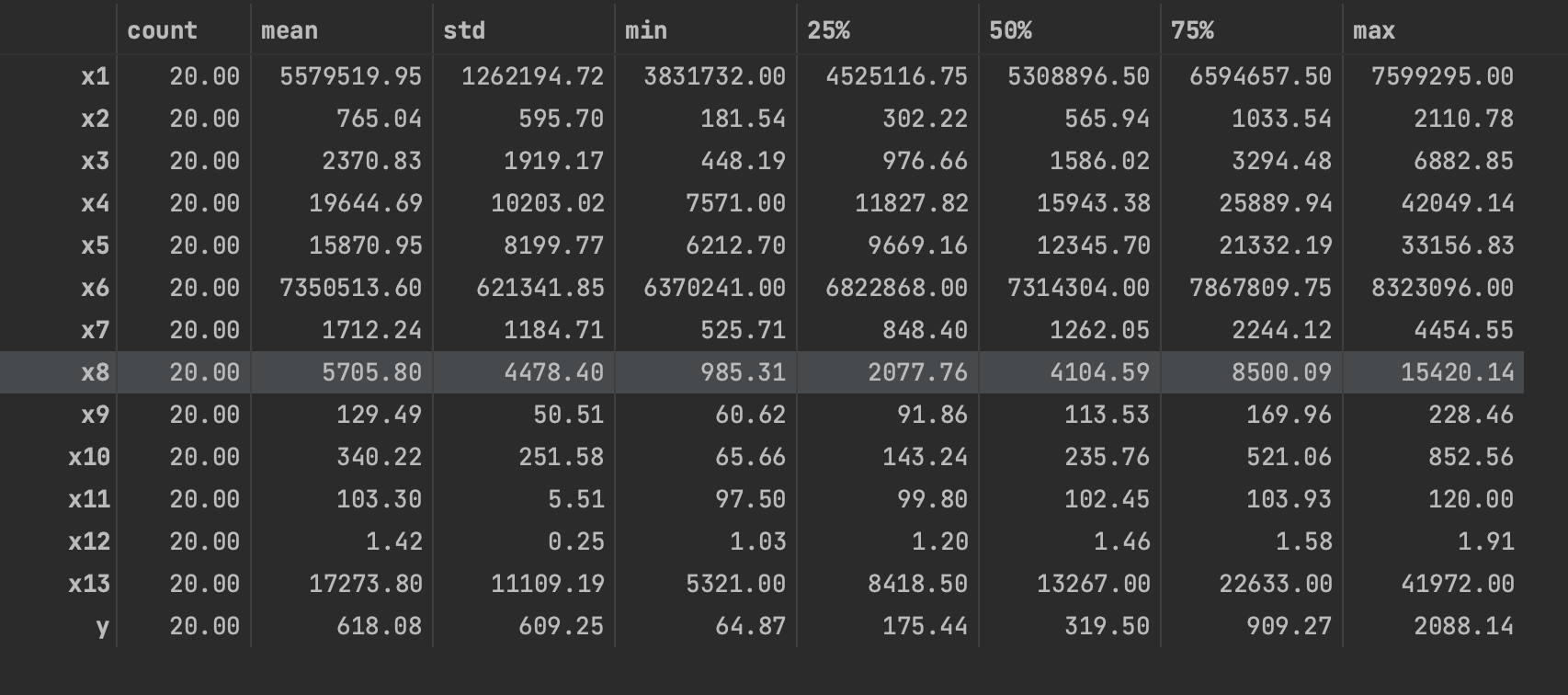
在这里插入图片描述

# 描述性分析
r = [data.min(), data.max(), data.mean(), data.std()]
r = pd.DataFrame(r, index=['Min', 'Max', 'Mean', 'STD']).T
r = np.round(r, 2)
r

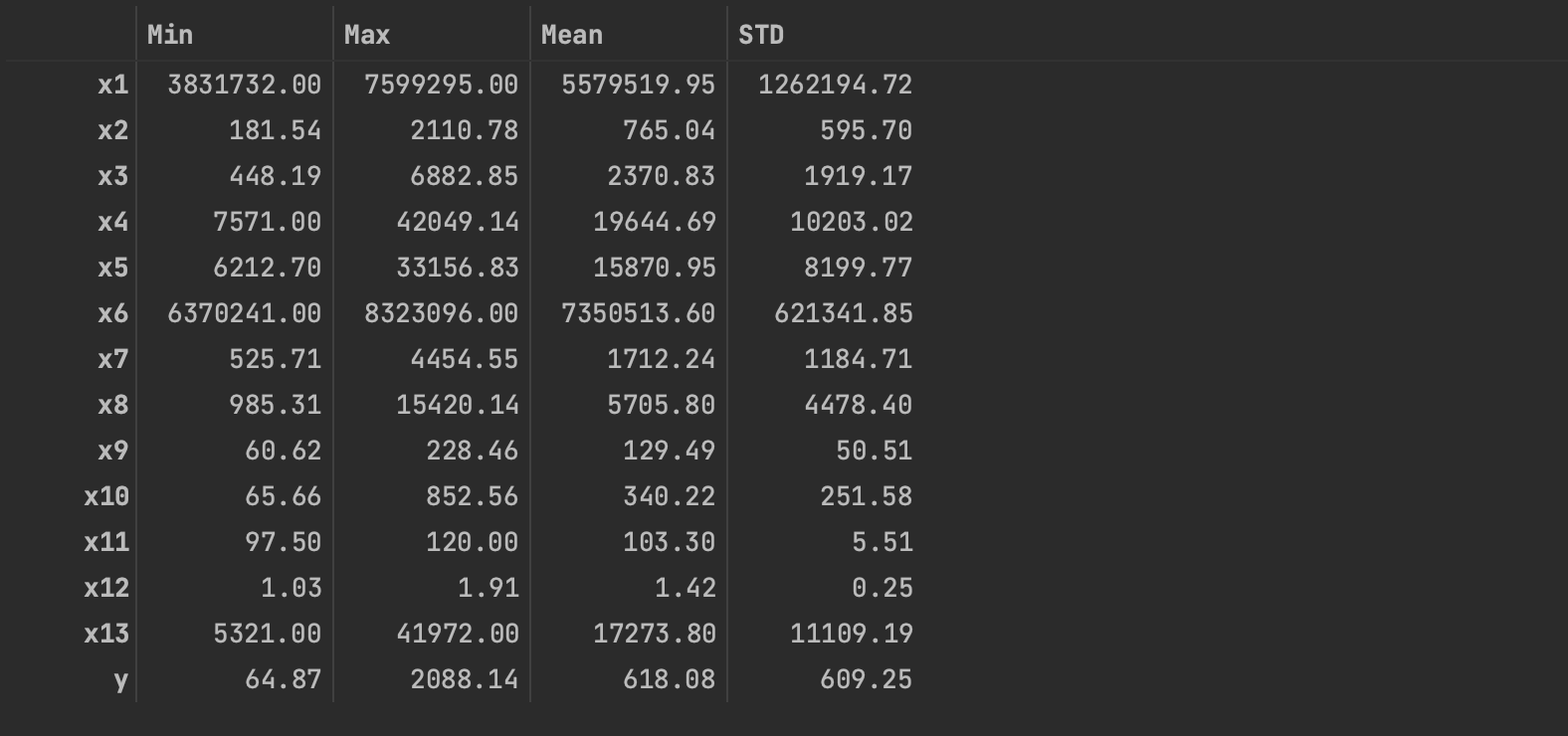
在这里插入图片描述

1.3 变量的分布情况

from sklearn.preprocessing import MinMaxScaler

#实现归一化
scaler = MinMaxScaler() #实例化
scaler = scaler.fit(data) #fit，在这里本质是生成min(x)和max(x)
data_scale = pd.DataFrame(scaler.transform(data)) #通过接口导出结果
data_scale.columns = data.columns

import joypy
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import cm
import seaborn as sns

fig, axes = joypy.joyplot(data_scale, alpha=.5, color='#FFCC99')#连续值的列为一个"脊"

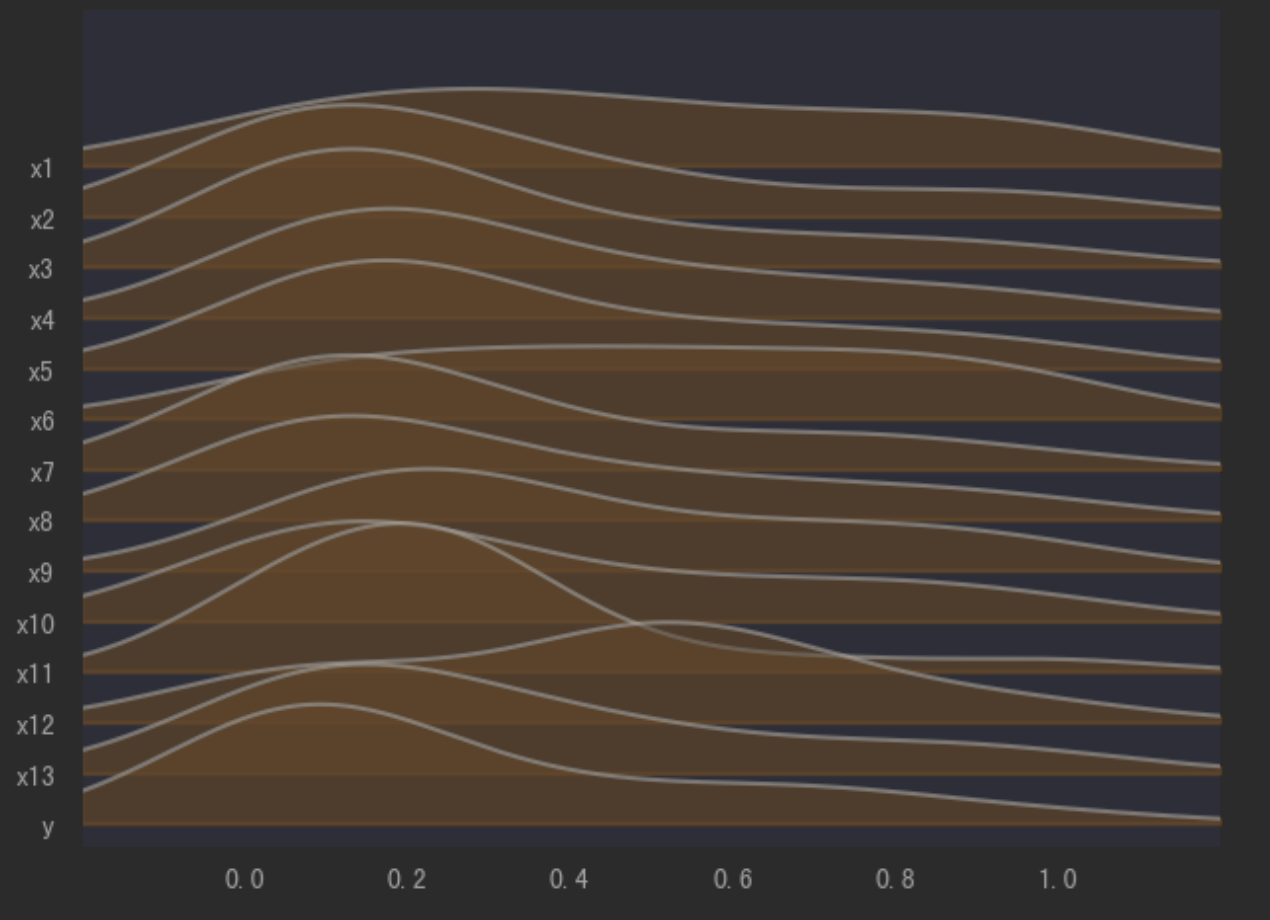
在这里插入图片描述

data_scale.plot()

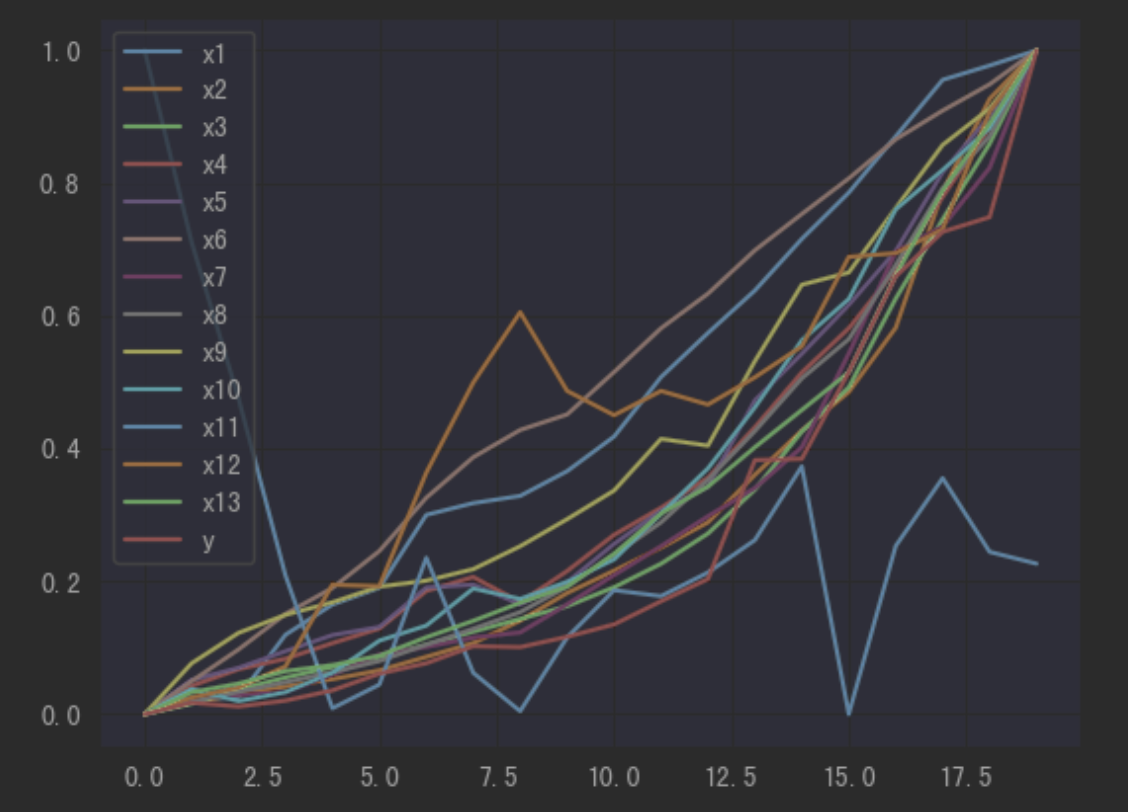
在这里插入图片描述

1.4 相关性分析

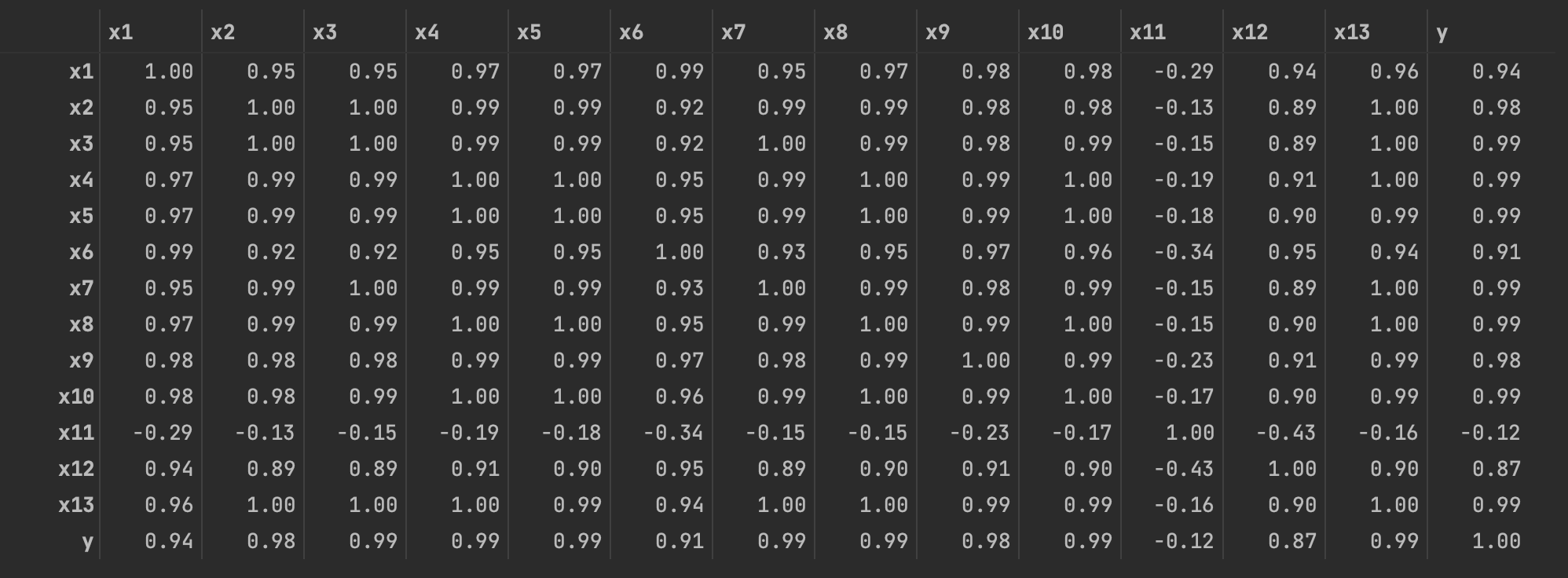
pear = np.round(data.corr(method = 'pearson'), 2)
pear

在这里插入图片描述

plt.figure(figsize=(12,12))
sns.heatmap(data.corr(), center=0,
            square=True, linewidths=.5, cbar_kws={"shrink": .5},annot=True, fmt='.1f')
#设置x轴
plt.xticks(fontsize=15)
#设置y轴
plt.yticks(fontsize=15)
plt.tight_layout()
plt.savefig('a.png')

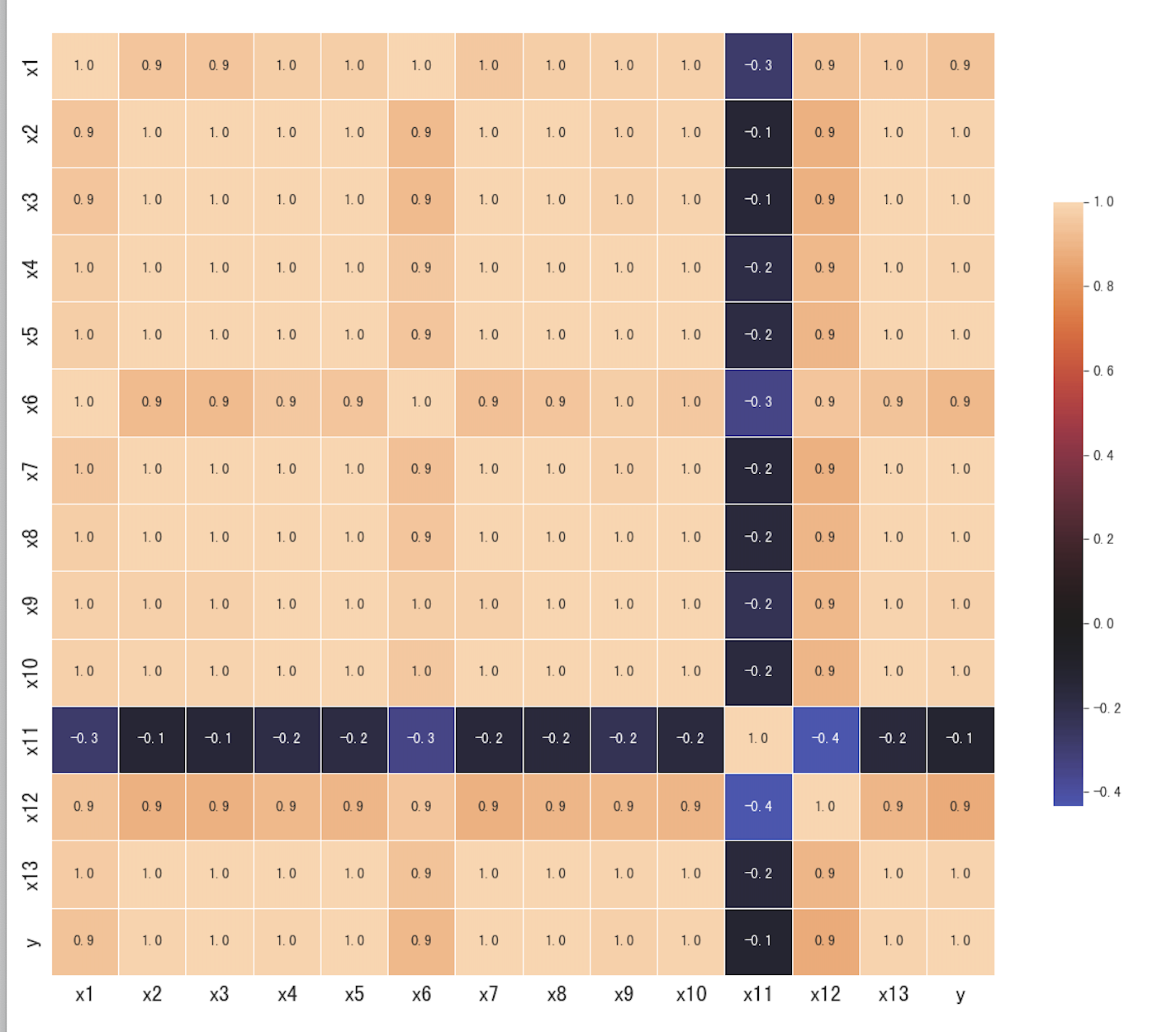
在这里插入图片描述

  • 由图可知，居民消费价格指数（x11）与财政收入的线性关系不显著，而且呈现负相关。其余变量均与财政收入呈现高度的正相关关系。

二、数据的预处理

  • 变量的筛选（分析方法的选择）：
    • 以往对财政收入的分析会使用 多元线性回归模型和最小二乘估计方法来估计回归模型的系数通过系数能否通过检验来检验它们之间的关系，但这样的结果对数据依赖程度很大，并且求得的往往只是局部最优解，后续的检验可能会失去应有的意义。
    • 因此本案例运用Adaptive-Lasso变量选择方法来研究,对于Lasso，这里参考书中的理论知识

2.1 Lasso变量选择模型

  • 这里没有找到AdaptiveLasso这个函数，用Lasso代替
from sklearn.linear_model import Lasso
model = Lasso(alpha=0.1, max_iter=100000)
model.fit(data.iloc[:, 0:13], data['y'])
q=model.coef_#各特征的系数
q=pd.DataFrame(q,index=data.columns[:-1])
q

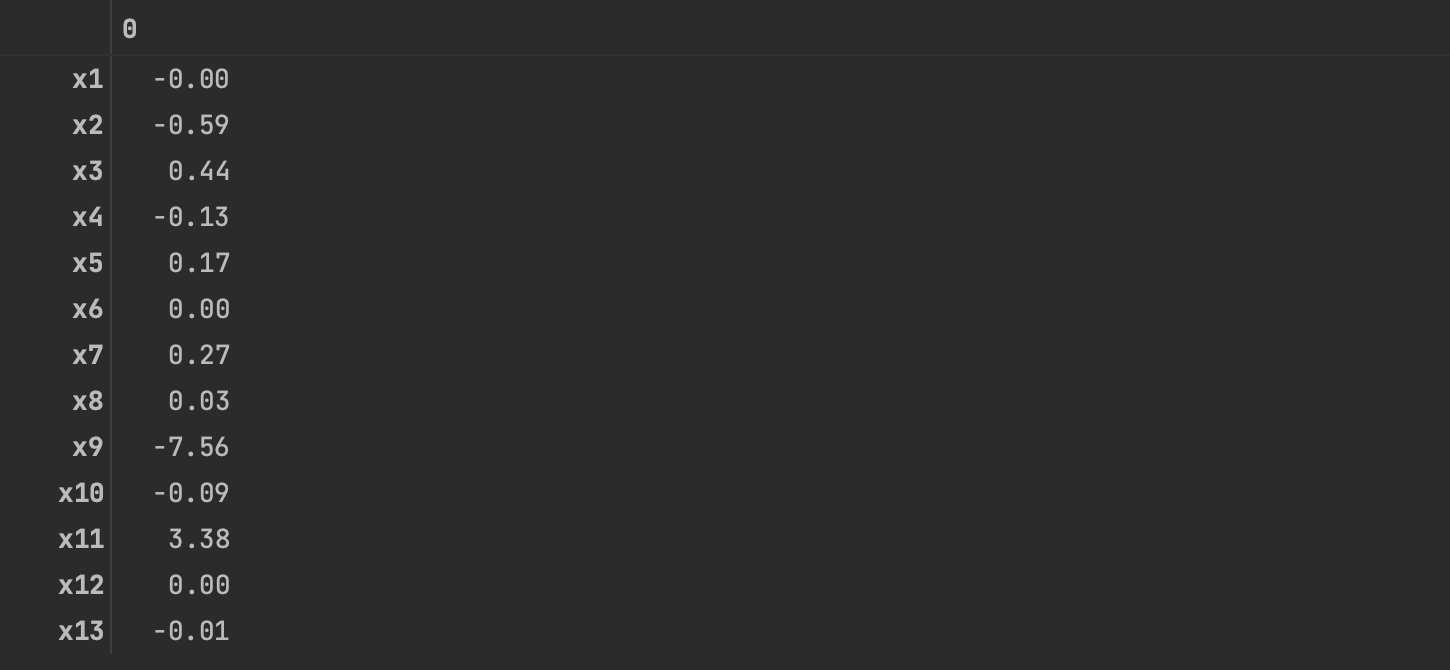
在这里插入图片描述

  • 计算出某变量的特征值非零，则表示该变量对预测变量存在较大影响，而如果某变量的特征值为零，则表示该变量对预测变量影响很小。
  • 调整参数值（参照：https://blog.csdn.net/weixin_43746433/article/details/100047231）
from sklearn.linear_model import Lasso
lasso = Lasso(1000)  #调用Lasso()函数，设置λ的值为1000
lasso.fit(data.iloc[:,0:13],data['y'])
print('相关系数为：',np.round(lasso.coef_,5))  #输出结果，保留五位小数
## 计算相关系数非零的个数
print('相关系数非零个数为：',np.sum(lasso.coef_ != 0))
mask = lasso.coef_ != 0  #返回一个相关系数是否为零的布尔数组
print('相关系数是否为零：',mask)

new_reg_data = data.iloc[:,:13].iloc[:,mask]  #返回相关系数非零的数据
new_reg_data = pd.concat([new_reg_data,data.y],axis=1)
new_reg_data.to_excel('new_reg_data.xlsx')

在这里插入图片描述

  • 根据非零的系数，最终通过Lasso筛选出的变量如下
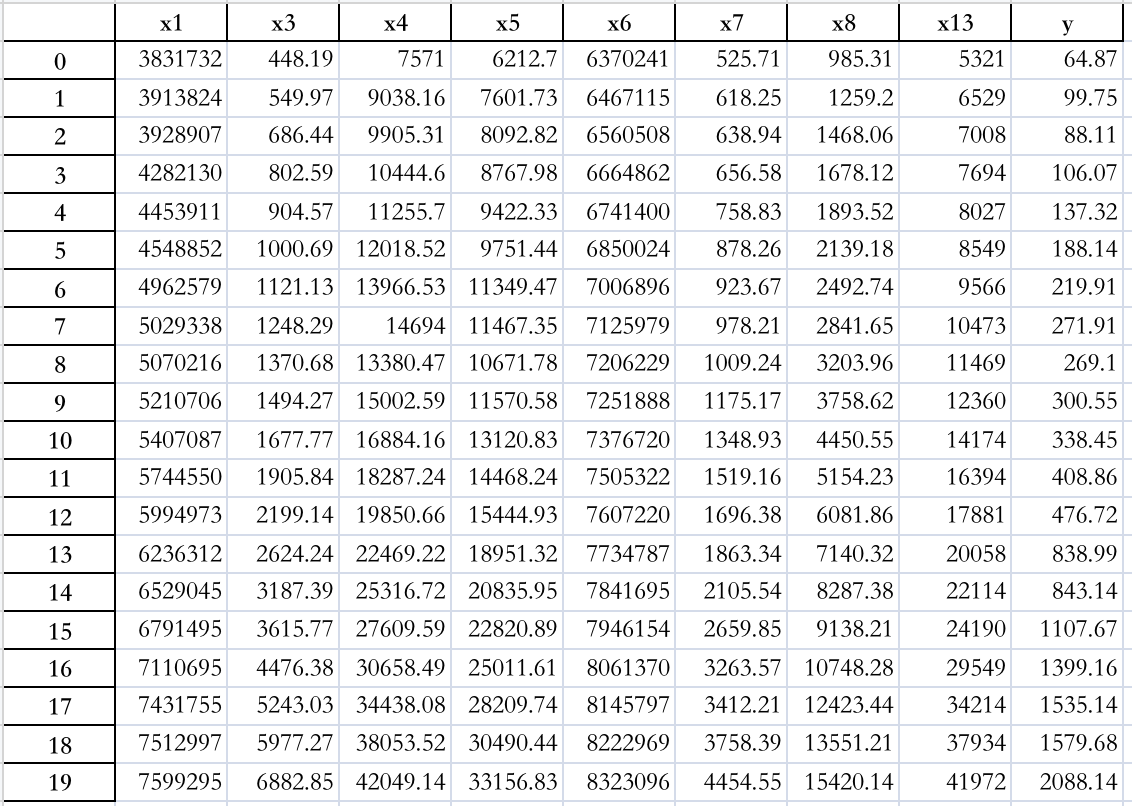
    在这里插入图片描述
  • 变量筛选好之后，接下来的开始建模

三、建立财政收入预测模型

在这里插入图片描述

3.1 灰色模型

  • 灰色模型学习：https://blog.csdn.net/qq_42374697/article/details/106611556
def GM11(x0): #自定义灰色预测函数
    import numpy as np
    x1 = x0.cumsum() # 生成累加序列
    z1 = (x1[:len(x1)-1] + x1[1:])/2.0 # 生成紧邻均值（MEAN）序列，比直接使用累加序列好，共 n-1 个值
    z1 = z1.reshape((len(z1),1))
    B = np.append(-z1, np.ones_like(z1), axis = 1)    # 生成 B 矩阵
    Y = x0[1:].reshape((len(x0)-1, 1))    # Y 矩阵
    [[a],[u]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Y)    #计算参数
    f = lambda k: (x0[0]-u/a)*np.exp(-a*(k-1))-(x0[0]-u/a)*np.exp(-a*(k-2))    #还原值
    delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)]))    # 计算残差
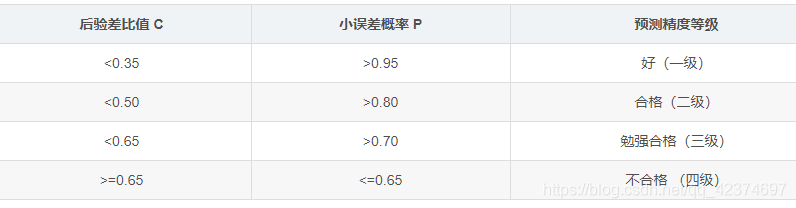
    C = delta.std()/x0.std()
    P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
    return f, a, u, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率

data.index = range(1994, 2014)
data.loc[2014] = None
data.loc[2015] = None

# 模型精度评价
# 被lasso筛选出来的6个变量
l = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']
for i in l:
    GM = GM11(data[i][list(range(1994, 2014))].values)
    f = GM[0]
    c = GM[-2]
    p = GM[-1]
    data[i][2014] = f(len(data)-1)
    data[i][2015] = f(len(data))
    data[i] = data[i].round(2)
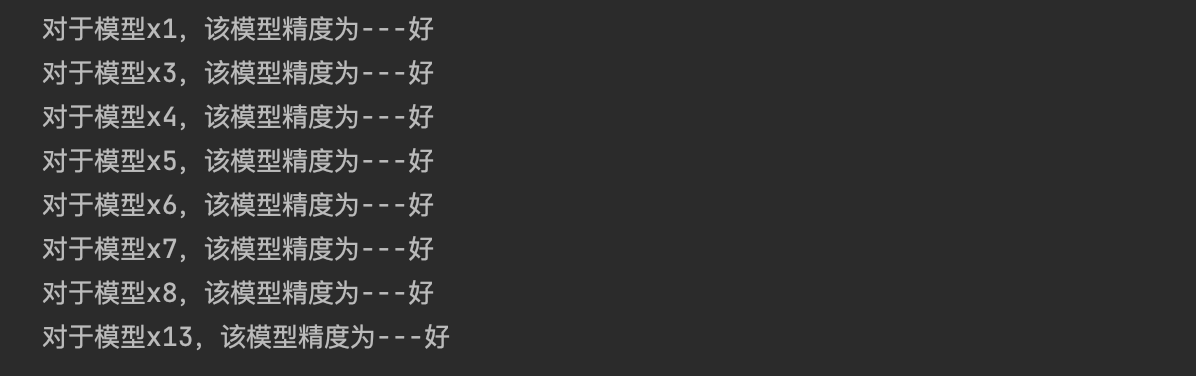
    if (c < 0.35) & (p > 0.95):
        print('对于模型{}，该模型精度为---好'.format(i))
    elif (c < 0.5) & (p > 0.8):
        print('对于模型{}，该模型精度为---合格'.format(i))
    elif (c < 0.65) & (p > 0.7):
        print('对于模型{}，该模型精度为---勉强合格'.format(i))
    else:
        print('对于模型{}，该模型精度为---不合格'.format(i))

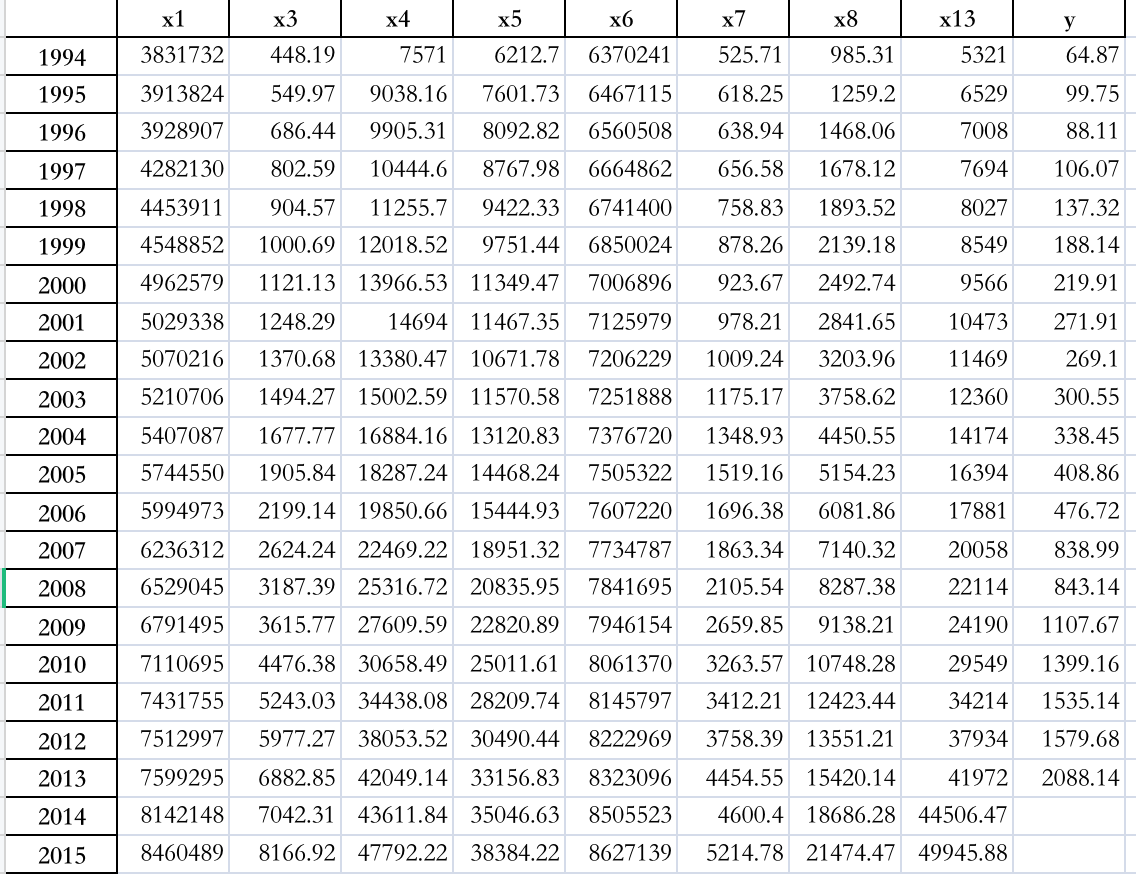
data[l+['y']].to_excel('data2.xlsx')

在这里插入图片描述
在这里插入图片描述

  • 预测值如下：

在这里插入图片描述

3.2 神经网络预测模型

  • 下面用历史数据建立神经网络模型
  • 其参数设置为误差精度107，学习次数10000次，神经元个数为Lasso变量选择方法选择的变量个数8。
'''神经网络'''
data2 = pd.read_excel('data2.xlsx', index_col=0)
# 提取数据
feature = list(data2.columns[:len(data2.columns)-1]) # ['x1', 'x2', 'x3', 'x4', 'x5', 'x7']
train = data2.loc[list(range(1994, 2014))].copy()
mean = train.mean()
std = train.std()
train = (train - mean) / std    # 数据标准化，这里使用标准差标准化
x_train = train[feature].values
y_train = train['y'].values

# 建立神经网络模型
from keras.models import Sequential
from keras.layers import Dense, Activation
import tensorflow

model = Sequential()
model.add(Dense(input_dim=8, units=12))
model.add(Activation('relu'))
model.add(Dense(input_dim=12, units=1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(x_train, y_train, epochs=10000, batch_size=16)
model.save_weights('net.model')

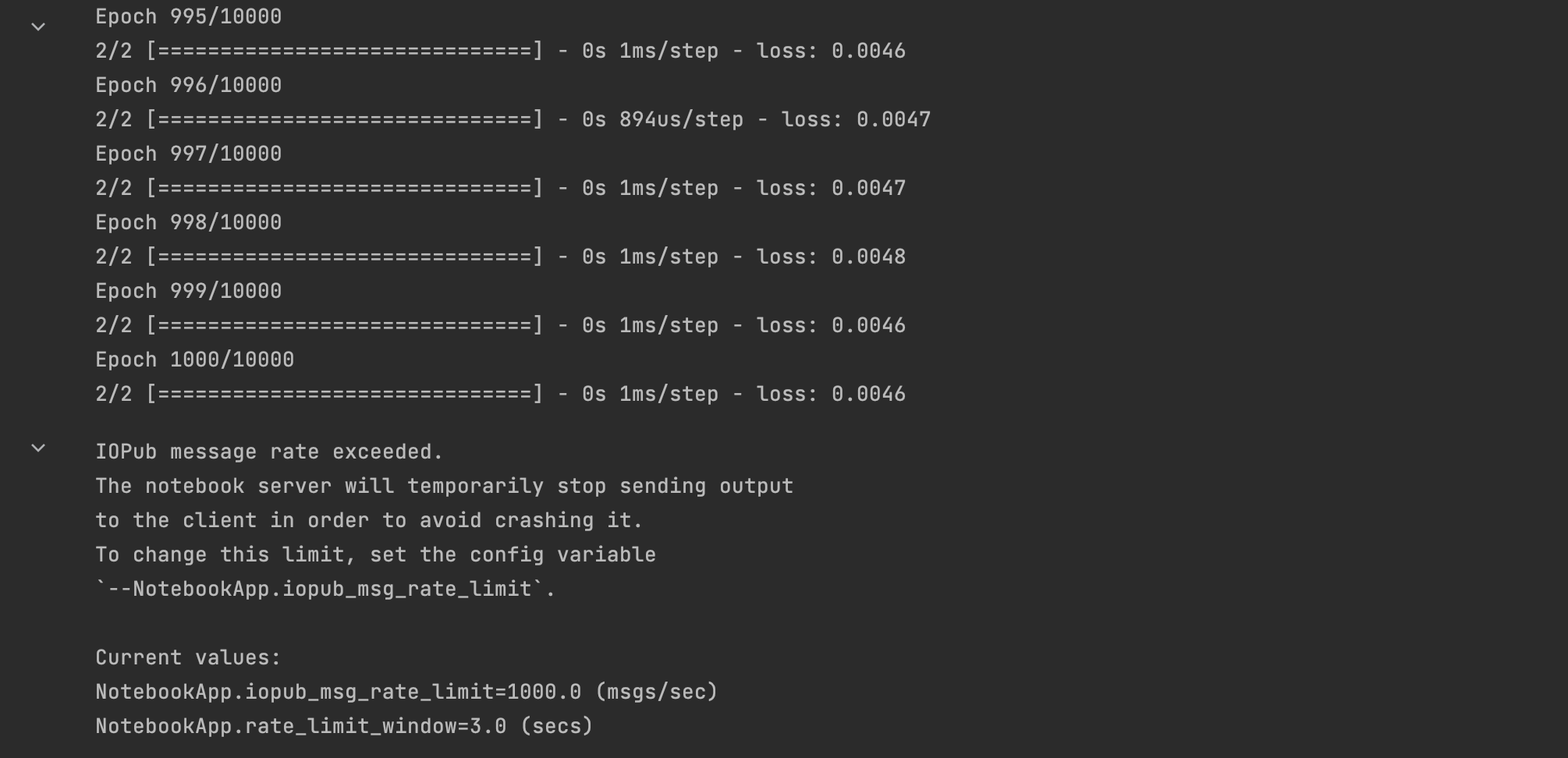
在这里插入图片描述

  • 训练好模型后，将1994 − 2005带入模型中做预测
# 将整个变量矩阵标准化
x = ((data2[feature] - mean[feature]) / std[feature]).values
# 预测，并还原结果
data2['y_pred'] = model.predict(x) * std['y'] + mean['y']
data2.to_excel('data3.xlsx')
  • 预测结果

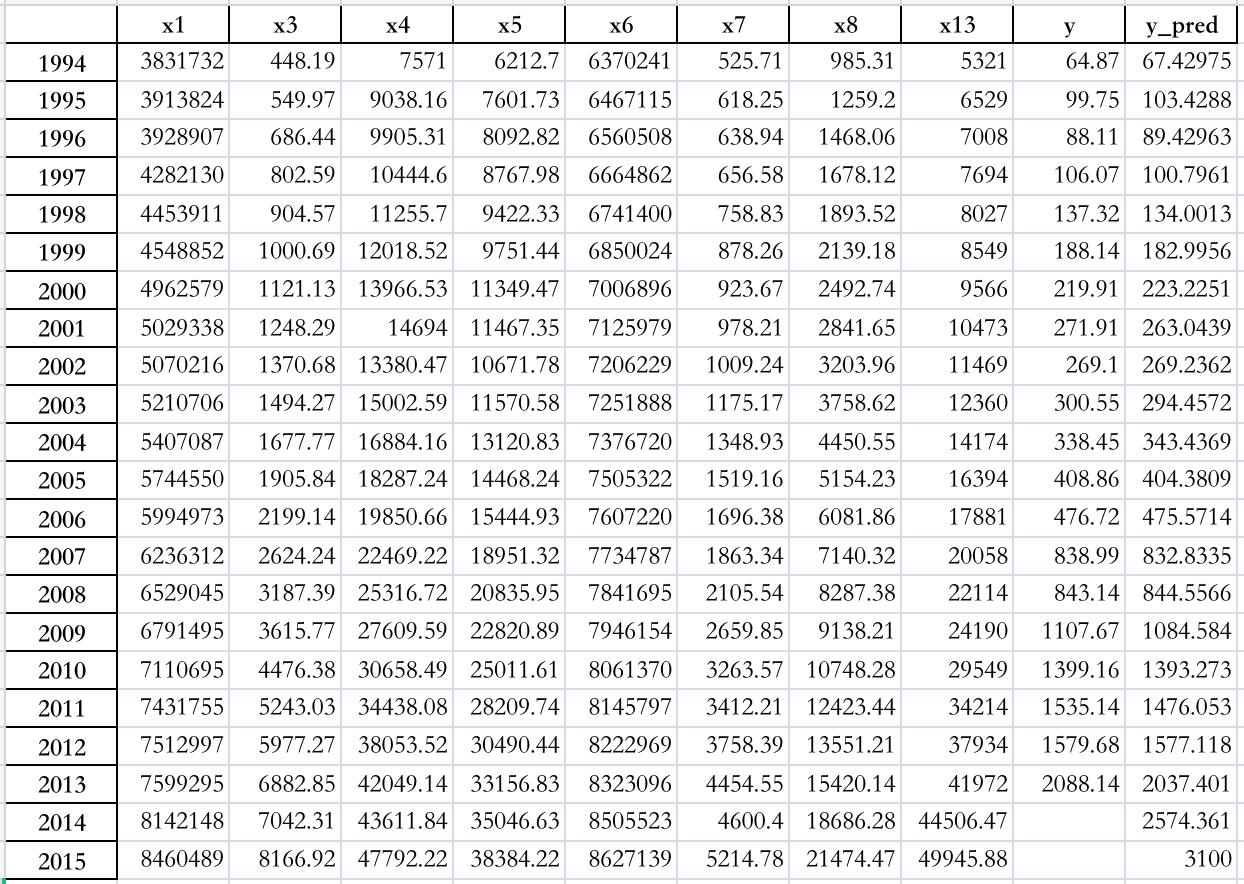
在这里插入图片描述

  • 绘制真实值与预测值之间的折线图
import matplotlib.pyplot as plt
p = data2[['y', 'y_pred']].plot(style=['b-o', 'r-*'])
p.set_ylim(0, 2500)
p.set_xlim(1993, 2016)
plt.show()
plt.savefig('plot.png')  # 保存图像为 plot.png

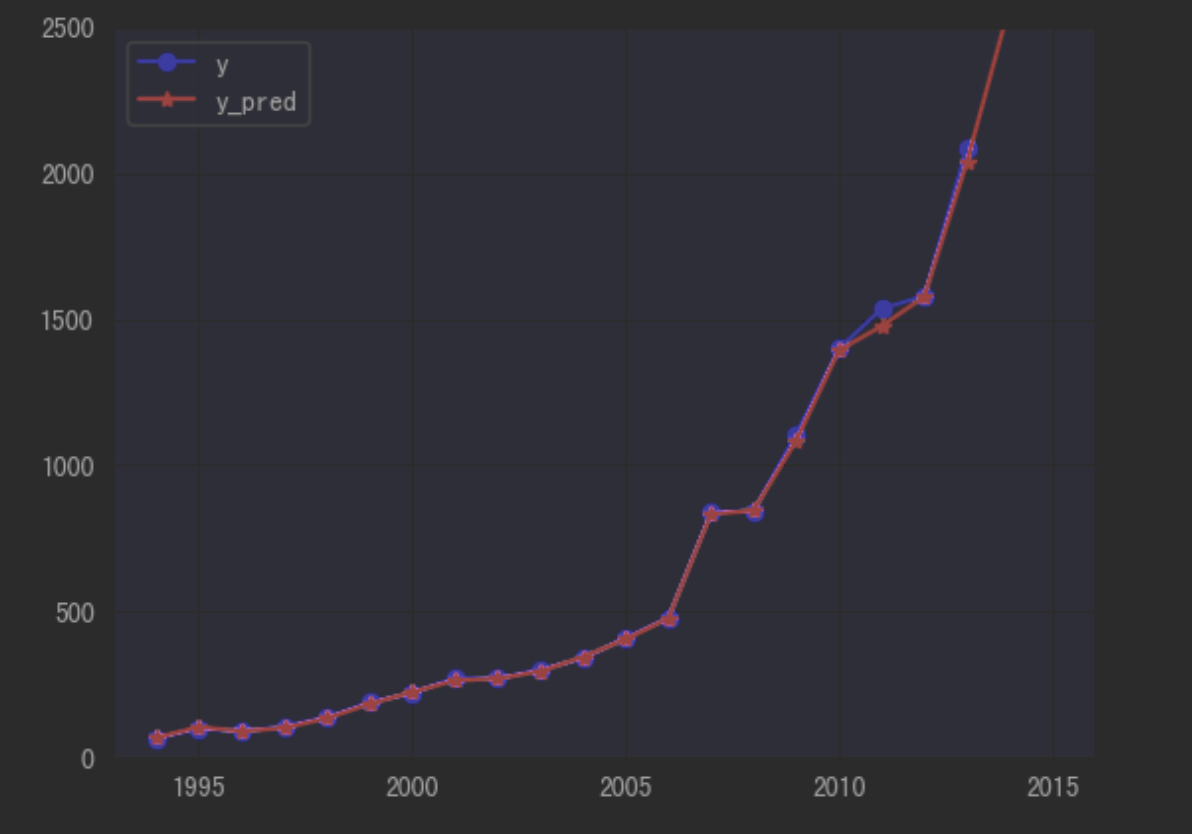
在这里插入图片描述

  • 从结果中，比较预测值与真实值基本高度吻合
  • 为了与神经网络预测结果有一个对比，下面使用其他预测模型查看其结果如何
from sklearn.linear_model import LinearRegression # 线性回归
from sklearn.neighbors import KNeighborsRegressor # K近邻回归
from sklearn.neural_network import MLPRegressor # 神经网络回归
from sklearn.tree import DecisionTreeRegressor # 决策树回归
from sklearn.tree import ExtraTreeRegressor # 极端随机森林回归
from xgboost import XGBRegressor # XGBoot
from sklearn.ensemble import RandomForestRegressor # 随机森林回归
from sklearn.ensemble import AdaBoostRegressor  # Adaboost 集成学习
from sklearn.ensemble import GradientBoostingRegressor # 集成学习梯度提升决策树
from sklearn.ensemble import BaggingRegressor # bagging回归
from sklearn.linear_model import ElasticNet

from sklearn.metrics import explained_variance_score,\
mean_absolute_error,mean_squared_error,\
median_absolute_error,r2_score

models=[LinearRegression(),KNeighborsRegressor(),MLPRegressor(alpha=20),DecisionTreeRegressor(),ExtraTreeRegressor(),XGBRegressor(),RandomForestRegressor(),AdaBoostRegressor(),GradientBoostingRegressor(),BaggingRegressor(),ElasticNet()]
models_str=['LinearRegression','KNNRegressor','MLPRegressor','DecisionTree','ExtraTree','XGBoost','RandomForest','AdaBoost','GradientBoost','Bagging','ElasticNet']


data2 = pd.read_excel('data2.xlsx', index_col=0)
# 提取数据
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']
train = data2.loc[list(range(1994, 2014))].copy()
mean = train.mean()
std = train.std()
train = (train - mean) / std    # 数据标准化，这里使用标准差标准化
x_train = train[feature].values
y_train = train['y'].values
# 将整个变量矩阵标准化
x = ((data2[feature] - mean[feature]) / std[feature]).values


for name,model in zip(models_str,models):
    print('开始训练模型：'+name)
    model=model   #建立模型
    a = 'y_pred_'+ name
    data2[a] = model.fit(x_train,y_train).predict(x) * std['y'] + mean['y']
    df=data2[:-2]
    print('平均绝对误差为：',mean_absolute_error(df['y'].values,df[a].values))
    print('均方误差为：',mean_squared_error(df['y'],df[a]))
    print('中值绝对误差为：',median_absolute_error(df['y'],df[a]))
    print('可解释方差值为：',explained_variance_score(df['y'],df[a]))
    print('R方值为：',r2_score(df['y'],df[a]))
    print('*-*'*15)

在这里插入图片描述

环境搭建

在这里插入图片描述

  • 安装成功后弹出镜像（否则无法正常安装）

在这里插入图片描述

# 设置中文字体
plt.rcParams['font.sans-serif'] = 'SimHei'

Spark pandsAPI接口（了解）

  • 使用Spark提供的pandsAPI接口进行数据处理
  • 处理操作同pands，略有不同
  • 适合处理大型数据（≥1M）

十分钟了解 Spark 上的 Pandas API（一）
注意，读取含有字符串的Excel文件时，需要指定Spark DataFrame的模式（schema），以确保每列的类型正确
无法关闭科学计数法

from pyspark.sql import SparkSession
import pyspark.pandas as ps

# 创建SparkSession
spark = SparkSession.builder.getOrCreate()

# 使用pandas读取Excel文件
pandas_df = ps.read_excel('./input/data.xlsx')
pandas_df = pandas_df.astype(str)

print(pandas_df)

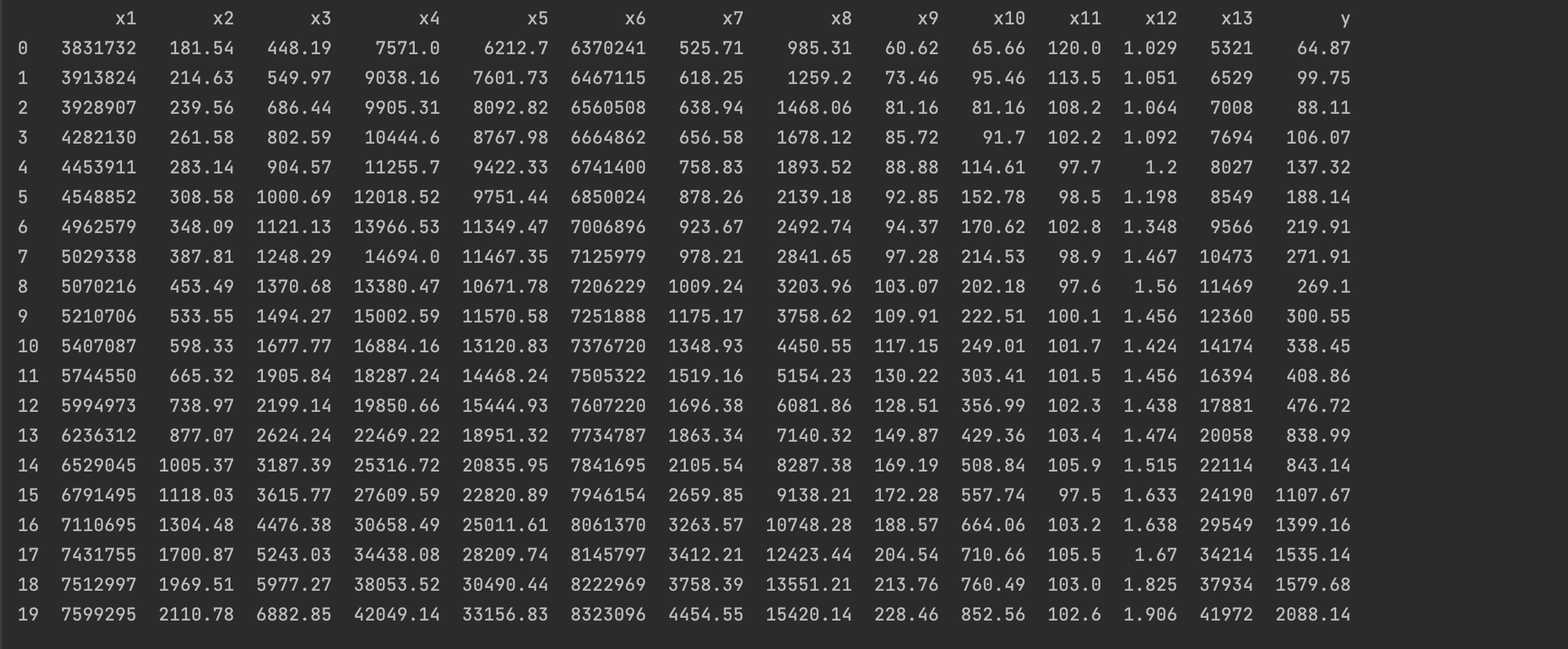
在这里插入图片描述

官方资料：Spark上的Pandas APD

分布式 + Spark进行数据处理

文件上传hdfs（分布存储）

Spark数据处理

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/705560.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

windows本地上传文件到服务器（scp）

windows本地上传文件到服务器（scp）

命令 1.ssh 用户名ip&#xff1a;远程登录服务器。 ssh root1.15.233.1932.scp 本地文件路径 用户名ip:上传路径 &#xff1a;本地文件与服务器进行传递。 scp C:\a.txt root1.15.233.193:/var/www/html3.本地文件夹上传到服务器 scp -r C:\user root1.15.233.193:/home4…
阅读更多...
三防工业平板在哪些行业中得到广泛应用？

三防工业平板在哪些行业中得到广泛应用？

随着科技的不断进步&#xff0c;工业平板正逐渐成为各行业中不可或缺的工具。其中&#xff0c;三防工业平板由于其卓越的耐用性和丰富的功能&#xff0c;在许多行业中得到了广泛的应用。本文将重点介绍三防工业平板在以下几个行业中的应用。 三防工业平板在物流行业中发挥着关键…
阅读更多...
shell脚本ssh远程执行命令给变量赋值的问题

shell脚本ssh远程执行命令给变量赋值的问题

需求及目标 从A机器通过SSH方式到B机器&#xff0c;并执行相关的命令。命令中包含变量及变量的赋值。 代码如下&#xff0c;意思是&#xff0c;ssh到10.111.111.27这台机器&#xff0c;cd到 / 根目录下&#xff0c;并执行ls命令&#xff0c;如果ls出来的结果不为空&#xff0…
阅读更多...
【鲁棒优化】微电网鲁棒优化定价方案研究（Matlab代码实现）

【鲁棒优化】微电网鲁棒优化定价方案研究（Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…
阅读更多...
【算法】区间DP （从记忆化搜索到递推DP）⭐

【算法】区间DP （从记忆化搜索到递推DP）⭐

文章目录 前期知识516. 最长回文子序列思路1——转换问题&#xff1a;求 s 和反转后 s 的 LCS&#xff08;最长公共子序列&#xff09;思路2——区间DP&#xff1a;从两侧向内缩小问题规模补充&#xff1a;记忆化搜索代码 1039. 多边形三角剖分的最低得分从记忆化搜索开始翻译成…
阅读更多...
改造3dmax的快捷键自定义3dmax快捷键

改造3dmax的快捷键自定义3dmax快捷键

快捷键需要整体规划&#xff0c;不然太乱了&#xff0c;不要担心你的自定义快捷键破坏了系统原有的快捷键&#xff0c;或者和原有的某些快捷键冲突&#xff0c;如果那些被系统定义的快捷键所对应的功能指令你都不知道他们是干什么用的&#xff0c;你要他们有什么用。还不如来得…
阅读更多...
Rust 基础入门 ——数值类型

Rust 基础入门 ——数值类型

数值类型 概述 数值类型 这里重点在于一些特殊的书写方式的格式&#xff0c;和几种特殊类型。除此以外&#xff0c;还包括一些常见的类型处理方式&#xff08;这之中包括了一些问题处理和Rust 特有内容&#xff09;。 细分之下为&#xff1a; 整数类型 重点问题&#xff1a…
阅读更多...
基于PyQt5的图形化界面开发——天气应用

基于PyQt5的图形化界面开发——天气应用

目录 0. 前言1. 注册心知天气2. 代码实现3. 其他PyQt5文章 0. 前言 本节使用PyQt5开发天气应用程序实现以下功能&#xff1a; 通过调用天气API获取实时天气数据&#xff0c;并在应用程序中显示当前城市的温度、天气状况、风速等信息。 操作系统&#xff1a;Windows10 专业版…
阅读更多...
关于 3.0 和 2.0 的数据文件差异以及性能优化思路

关于 3.0 和 2.0 的数据文件差异以及性能优化思路

如果需要对数据库性能优化&#xff0c;了解数据文件的存储方式和工作原理是必要的。 对于时序数据库&#xff08;Time Series Database&#xff09; TDengine 来说&#xff0c;在 2.x 版本中时序数据的保留策略是由keep和days这两个参数把控的。&#xff08;详情可见&#xff…
阅读更多...
云原生——Kubenetes基础

云原生——Kubenetes基础

❄️作者介绍&#xff1a;奇妙的大歪❄️ &#x1f380;个人名言&#xff1a;但行前路&#xff0c;不负韶华&#xff01;&#x1f380; &#x1f43d;个人简介&#xff1a;云计算网络运维专业人员&#x1f43d; 目录 一.什么是Kubernetes&#xff1f; 二.为什么你需要 Kubern…
阅读更多...
markdown数学公式总结

markdown数学公式总结

行内与独行 行内公式&#xff1a;将公式插入到本行内&#xff0c;符号&#xff1a; 公式内容 公式内容 公式内容&#xff0c;如&#xff1a; x y z xyz xyz 独行公式&#xff1a;将公式插入到新的一行内&#xff0c;并且居中&#xff0c;符号&#xff1a; 公式内容 公式内容 公…
阅读更多...
RISC-V IDE MRS使用笔记(十)：嵌入式编程开发技巧汇总

RISC-V IDE MRS使用笔记(十)：嵌入式编程开发技巧汇总

RISC-V IDE MRS使用笔记(十)&#xff1a;嵌入式编程开发技巧汇总 MRS常见嵌入式开发技巧: Q1&#xff1a;如何修改程序编译生成库&#xff1f; A1&#xff1a;在工具栏中点击活动工程的编译配置按钮&#xff0c;在Build Artifact的Tab页面指定目标类型&#xff0c;选中为Stat…
阅读更多...
uniapp仿浙北惠生活微信小程序

uniapp仿浙北惠生活微信小程序

最近给公司写了一个内部微信小程序&#xff0c;功能比较简单&#xff0c;之前是用微信小程序原声写的&#xff0c;一遍看文档一边写&#xff0c;js&#xff0c;wxml&#xff0c;wxcc&#xff0c;json分在不同文件的写法很不习惯&#xff0c;于是花了两天用uniapp重写了一遍&…
阅读更多...
思维导图对我生活以及工作的帮助（用户投稿）

思维导图对我生活以及工作的帮助（用户投稿）

作为一名白领&#xff0c;我每天都面临着各种各样的工作和生活压力。 为了更好地应对这些挑战&#xff0c;我开始尝试使用思维导图来帮助自己更好地组织和管理各种信息和任务。其中一款非常优秀的软件就是ProcessOn思维导图&#xff0c;它为我的工作和生活带来了很多便利和帮助…
阅读更多...
Spring Boot|启动图案修改ASCII字符画

Spring Boot|启动图案修改ASCII字符画

效果图 实现 在项目目录的resources文件夹中新建一个banner.txt&#xff0c;将内容放入即可&#xff1a; // _ooOoo_ // // o8888888o // // …
阅读更多...
华为ENSP配置无线AC-网关模式

华为ENSP配置无线AC-网关模式

1、配置交换机以及AC的接口为trunk 交换机 vlan b 10 20 # interface GigabitEthernet0/0/1port link-type trunkport trunk allow-pass vlan 10 20 # # interface GigabitEthernet0/0/2port link-type trunkport trunk pvid vlan 10port trunk allow-pass vlan 10 20 # …
阅读更多...
Linux系统安装QQ最新版 2023-06-30

Linux系统安装QQ最新版 2023-06-30

腾讯在2023-05-30更新了linux版的qq&#xff0c;这次界面终于不再复古&#xff0c;好看多了。 安装步骤&#xff1a; 1.进入官网&#xff0c;寻找合适的安装包下载 https://im.qq.com/linuxqq/index.shtml 选择跟自己计算机匹配的版本&#xff0c;一般都是X86&#xff0c;如…
阅读更多...
JAVA-编程基础-05-方法的定义、调用、重载

JAVA-编程基础-05-方法的定义、调用、重载

Lison <dreamlison163.com>, v1.0.0, 2023.03.22 JAVA-编程基础-05-方法的定义、调用、重载 文章目录 JAVA-编程基础-05-方法的定义、调用、重载方法的概念什么是方法 方法的定义和调用无参数方法定义和调用方法调用过程图解 带参数方法的定义和调用带返回值方法的定义和…
阅读更多...
Ureport 多数据集合关联显示

Ureport 多数据集合关联显示

ureport 使用较少&#xff0c;目前单位这边有项目正好使用到了&#xff0c;也遇到不少坑&#xff0c;和其他报表稍微有些不同&#xff0c;在这里记录一下&#xff0c;为大家排一下坑 目前需求是要求数据以这样显示 1、创建数据源 1.1 B2、C1、D2 、C4、C2 各使用了不同的数据…
阅读更多...
chatGPT流式回复是怎么实现的

chatGPT流式回复是怎么实现的

chatGPT流式回复是怎么实现的 先说结论&#xff1a; chatGPT的流式回复用的就是HTTP请求方案中的server-send-event流式接口&#xff0c;也就是服务端向客户端推流数据。 那eventStream流式接口怎么实现呢&#xff0c;下面就进入正题&#xff01; 文章目录 chatGPT流式回复…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023