数值类型

概述

数值类型 这里重点在于一些特殊的书写方式的格式，和几种特殊类型。除此以外，还包括一些常见的类型处理方式（这之中包括了一些问题处理和Rust 特有内容）。

细分之下为：

1. 整数类型
   1. 重点问题：溢出
2. 浮点数类型
   1. 重点类型：浮点数陷阱
3. 运算
   1. 数字运算
   2. 位运算
4. 序列
5. 有理数和复数（我的图形计算和数据计算可算省事了>_<）

整形

首先的是 一些特殊的整形表示方式。
在Rust中，我们是可以在数字中通过 下划线，来优化阅读体验的。毕竟一千万或者一亿还要自己数零也太让人眼花了吧。
具体实例如下：

let zry:i64 =  1000_0000_0000; // 这里的区分完全按照个人喜好，我喜欢四个一组正好按习惯区分，三位的还要转换一下不方便。

然后是取决于计算机处理器类型的特殊类型
在rust 中我们除去可以手动标定选择哪一种类型长度，还可以将这个过程交给处理器（CPU）。 这就是 size类型。 而在rust 中将类型简化，你可以认为 有几种类型，每种可以涉及正负号的类型都有有符号和无符号两种。
因此，我们可以推理出， 视架构而定的类型有 isize(有符号类型)usize（无符号类型）。

应用场景： isize 和 usize 的主要应用场景是用作集合的索引。

最后说一下类型定义的统一形式：有无符号 + 类型大小（位数）。
无符号数表示数字只能取正数，而有符号则表示数字既可以取正数又可以取负数。 有符号数字以 补码 形式存储。

长度	有符号类型	无符号类型
8 位	i8	u8
16 位	i16	u16
32 位	i32	u32
64 位	i64	u64
128 位	i128	u128
视架构而定	isize	usize

类型的存储范围计算规则
每个有符号类型规定的数字范围是 -(2^{n - 1}) ~ 2^{n -
1} - 1，其中 n 是该定义形式的位长度。因此 i8 可存储数字范围是 -(2⁷) ~ 2⁷ - 1，即 -128 ~ 127。无符号类型可以存储的数字范围是 0 ~ 2ⁿ - 1，所以 u8 能够存储的数字为 0 ~ 2⁸ - 1，即 0 ~ 255。

默认的整型
Rust 整型默认使用 i32，例如 let i = 1，那 i 就是 i32 类型，因此你可以首选它，同时该类型也往往是性能最好的。

多进制的表述方式
当然我们在C++ 中最喜欢的 0x00 清理内存时使用值。就有 十六进制表示法。
因此在Rust 中同样也有，针对不同的类型，有类似 C++ 的表示方式。具体展示如下：

数字字面量	示例
十进制	98_222
十六进制	0xff
八进制	0o77
二进制	0b1111_0000
字节 (仅限于 u8)	b'A'

整型溢出

在编程语言中，计算时常常会遇到一个问题，在长期运行后会遇到原有的空间不能存放运行结果的问题。即整型溢出。

在rust中，我们同样会遇到这个问题。 不过作为自称严格的开发语言，他会在调试模式下直接告诉你说：不行，这个东西你不能用。 （但要是你用 --release 那就没这优待了，都要投产了还给你做测试。开发人员总要有点自我要求啊）。

总结一下：

• 在 debug 模式编译时，Rust 会检查整型溢出，若存在这些问题，则使程序在编译时 panic(崩溃,Rust 使用这个术语来表明程序因错误而退出)。
• 使用 --release 参数进行 release 模式构建时，Rust 不检测溢出。相反，当检测到整型溢出时，Rust 会按照补码循环溢出（two’s complement wrapping）的规则处理。
  • 简而言之，大于该类型最大值的数值会被补码转换成该类型能够支持的对应数字的最小值。比如在 u8 的情况下，256 变成 0，257 变成 1，
    • 依此类推。程序不会 panic，但是该变量的值可能不是你期望的值。
    • 依赖这种默认行为的代码都应该被认为是错误的代码。

我们总不能提出问题不给解决方案的小喷子。所以解决这样的问题怎么做呢：
显示处理可能的溢出
使用标准库针对原始数字类型提供的这些方法：

• 使用 wrapping_* 方法在所有模式下都按照补码循环溢出规则处理，例如 wrapping_add

fn main() {
    let a : u8 = 255;
    let b = a.wrapping_add(20);
    println!("{}", b);  // 19
}

• 如果使用 checked_* 方法时发生溢出，则返回 None 值

fn main() {
    let a: u8 = 200;
    let b: u8 = 100;
    
    let result = a.checked_add(b);
    
    match result {
        Some(value) => println!("The sum is: {}", value),
        None => println!("Overflow occurred"),
    }
}

• 使用 overflowing_* 方法返回该值和一个指示是否存在溢出的布尔值

fn main() {
    let a: u8 = 200;
    let b: u8 = 100;
    
    let (result, overflow) = a.overflowing_add(b);
    
    if overflow {
        println!("Overflow occurred");
    } else {
        println!("The sum is: {}", result);
    }
}

• 使用 saturating_* 方法使值达到最小值或最大值

fn main() {
    let a: u8 = 250;
    let b: u8 = 10;
    
    let result = a.saturating_add(b);
    
    println!("The sum is: {}", result);
}

浮点数

在浮点数这一节，我们对类型本身的书写没有过多的解释，f32 、f64、是他可用的两种类型，没有无符号类型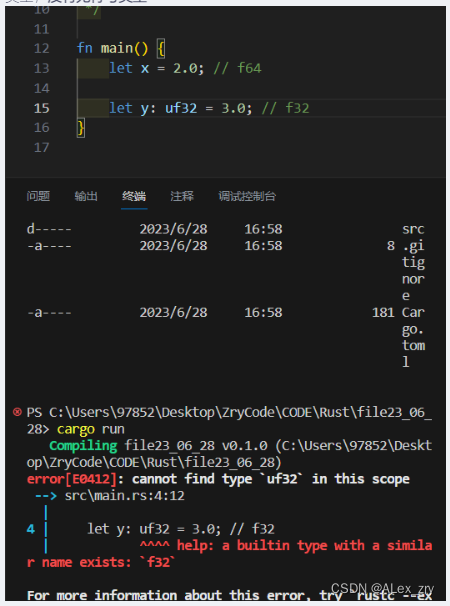

接下来重点在于浮点陷阱：
所谓的浮点陷阱是指，在rust 中的浮点并非真正意义的完全精确，只是我们通过一系列的手段给了它足够的精度。也就是说超过了它的精度保证区，就会出现异常。

举例

fn main(){
    let zry = 2.0; //默认的是使用 f64格式
    let z: f32 = 3.0; // f32

    let abc: (f32, f32, f32) = (0.1, 0.2, 0.3);
    let xyz: (f64, f64, f64) = (0.1, 0.2, 0.3);

    println!("abc (f32)");
    println!("   0.1 + 0.2: {:x}", (abc.0 + abc.1).to_bits());
    println!("         0.3: {:x}", (abc.2).to_bits());
    println!();

    println!("xyz (f64)");
    println!("   0.1 + 0.2: {:x}", (xyz.0 + xyz.1).to_bits());
    println!("         0.3: {:x}", (xyz.2).to_bits());
    println!();

    assert!(abc.0 + abc.1 == abc.2);
    assert!(xyz.0 + xyz.1 == xyz.2);
}

abc (f32)
   0.1 + 0.2: 3e99999a
         0.3: 3e99999a

xyz (f64)
   0.1 + 0.2: 3fd3333333333334
         0.3: 3fd3333333333333

thread 'main' panicked at 'assertion failed: xyz.0 + xyz.1 == xyz.2',
➥ch2-add-floats.rs.rs:14:5
note: run with `RUST_BACKTRACE=1` environment variable to display
➥a backtrace

对 f32 类型做加法时，0.1 + 0.2 的结果是 3e99999a，0.3 也是 3e99999a，因此 f32 下的 0.1 + 0.2 == 0.3 通过测试，但是到了 f64 类型时，结果就不一样了，因为 f64 精度高很多，因此在小数点非常后面发生了一点微小的变化，0.1 + 0.2 以 4 结尾，但是 0.3 以3结尾，这个细微区别导致 f64 下的测试失败了，并且抛出了异常。

如果非要进行比较呢？可以考虑用这种方式 (0.1_f64 + 0.2 - 0.3).abs() < 0.00001 ，具体小于多少，取决于你对精度的需求。

为了避免上面说的两个陷阱，你需要遵守以下准则：

• 避免在浮点数上测试相等性
• 当结果在数学上可能存在未定义时，需要格外的小心

总结一下

浮点数由于底层格式的特殊性，导致了如果在使用浮点数时不够谨慎，就可能造成危险，有两个原因：

1. 浮点数往往是你想要数字的近似表达 浮点数类型是基于二进制实现的，但是我们想要计算的数字往往是基于十进制，例如 0.1 在二进制上并不存在精确的表达形式，但是在十进制上就存在。这种不匹配性导致一定的歧义性，更多的，虽然浮点数能代表真实的数值，但是由于底层格式问题，它往往受限于定长的浮点数精度，如果你想要表达完全精准的真实数字，只有使用无限精度的浮点数才行

2. 浮点数在某些特性上是反直觉的 例如大家都会觉得浮点数可以进行比较，对吧？是的，它们确实可以使用 >，>= 等进行比较，但是在某些场景下，这种直觉上的比较特性反而会害了你。因为 f32 ， f64 上的比较运算实现的是 std::cmp::PartialEq 特征(类似其他语言的接口)，但是并没有实现 std::cmp::Eq 特征，但是后者在其它数值类型上都有定义，说了这么多，可能大家还是云里雾里，用一个例子来举例：

Rust 的 HashMap 数据结构，是一个 KV 类型的 Hash Map 实现，它对于 K 没有特定类型的限制，但是要求能用作 K 的类型必须实现了 std::cmp::Eq 特征，因此这意味着你无法使用浮点数作为 HashMap 的 Key，来存储键值对，但是作为对比，Rust 的整数类型、字符串类型、布尔类型都实现了该特征，因此可以作为 HashMap 的 Key。

NaN 不是NULL 的新一种未定义代称

首先我们再次复习一下，rust 的类型是被包装之后的。所以其原生的带着一些可供操作的API接口。
因此我们可以有这样的写法：

fn main() {
  let x = (-42.0_f32).sqrt();
  assert_eq!(x, x);
}

执行结果：

Compiling playground v0.0.1 (/playground)  
Finished dev [unoptimized + debuginfo] target(s) in 0.55s  
Running `target/debug/playground`  
thread 'main' panicked at 'assertion failed: `(left == right)`  
left: `NaN`,  
right: `NaN`', src/main.rs:3:3  
note: run with `RUST_BACKTRACE=1` environment variable to display a backtrace

对于数学上未定义的结果，例如对负数取平方根 -42.1.sqrt() ，会产生一个特殊的结果：Rust 的浮点数类型使用 NaN (not a number)来处理这些情况。

出于防御性编程的考虑，可以使用 is_nan() 等方法，可以用来判断一个数值是否是 NaN ：

fn main() {
    let x = (-42.0_f32).sqrt();
    if x.is_nan() {
        println!("未定义的数学行为")
    }
}

运算

数字运算

在rust 中的数字运算，依旧是传统意义上的加减乘除四则运算，然后是取模求余运算，
注意，不同类型是不可以混合计算的，否则会出现这样的结果报错!

位运算

Rust的运算基本上和其他语言一样

运算符	说明
& 位与	相同位置均为1时则为1，否则为0
| 位或	相同位置只要有1时则为1，否则为0
^ 异或	相同位置不相同则为1，相同则为0
! 位非	把位中的0和1相互取反，即0置为1，1置为0
<< 左移	所有位向左移动指定位数，右位补0
>> 右移	所有位向右移动指定位数，带符号移动（正数补0，负数补1）

fn main() {
    // 二进制为00000010
    let a:i32 = 2;
    // 二进制为00000011
    let b:i32 = 3;

    println!("(a & b) value is {}", a & b);

    println!("(a | b) value is {}", a | b);

    println!("(a ^ b) value is {}", a ^ b);

    println!("(!b) value is {} ", !b);

    println!("(a << b) value is {}", a << b);

    println!("(a >> b) value is {}", a >> b);

    let mut a = a;
    // 注意这些计算符除了!之外都可以加上=进行赋值 (因为!=要用来判断不等于)
    a <<= b;
    println!("(a << b) value is {}", a);
}

序列

Rust 提供了一个非常简洁的方式，用来生成连续的数值，例如 1..5，生成从 1 到 4 的连续数字，不包含 5 ；1..=5，生成从 1 到 5 的连续数字，包含 5，它的用途很简单，常常用于循环中：

for i in 1..=5 {
    println!("{}",i);
}

最终程序输出:

1
2
3
4
5

序列只允许用于数字或字符类型，原因是：它们可以连续，同时编译器在编译期可以检查该序列是否为空，字符和数字值是 Rust 中仅有的可以用于判断是否为空的类型。如下是一个使用字符类型序列的例子：

for i in 'a'..='z' {
    println!("{}",i);
}

有理数和复数

rust 对有理数和复数进行了支持，但是目前不在标准库中，需要我们显式说明加载对应工具库。

按照以下步骤来引入 num 库：

1. 创建新工程 cargo new complex-num && cd complex-num
2. 在 Cargo.toml 中的 [dependencies] 下添加一行 num = "0.4.0"
3. 将 src/main.rs 文件中的 main 函数替换为下面的代码
4. 运行 cargo run

use num::complex::Complex;

 fn main() {
   let z = Complex { re: 2.1, im: -1.2 };
   let r = Complex::new(11.1, 22.2);
   let y = z + r;

   println!("{} + {}i", y.re, y.im)
 }

运行结果：

downloaded部分是只在初次运行时使用的。后面就没有了。

总结

1. 整数类型：

   • 有符号类型：i8、i16、i32、i64、i128、isize，表示带有正负号的整数。
   • 无符号类型：u8、u16、u32、u64、u128、usize，表示非负整数。
   • 整数类型的范围取决于位数，例如i8可以表示范围为-128到127的整数。

2. 浮点数类型：

   • f32和f64，分别表示32位和64位的浮点数。
   • 浮点数在表示小数时具有一定的精度限制，可能存在舍入误差。

3. NaN类型

4. 运算：

   1. 数值运算
   2. 位运算
      • 位与（&）：相同位置均为1时结果为1，否则为0。
      • 位或（|）：相同位置只要有1时结果为1，否则为0。
      • 异或（^）：相同位置不相同结果为1，相同结果为0。
      • 位非（!）：将位中的0和1相互取反。
      • 左移（<<）：将所有位向左移动指定位数，右侧补0。
      • 右移（>>）：将所有位向右移动指定位数，带符号移动（正数补0，负数补1）。

5. 序列（Range）：

   • 使用..表示左闭右开的序列，例如1..5表示从1到4的连续数字。
   • 使用..=表示左闭右闭的序列，例如1..=5表示从1到5的连续数字。

6. 有理数和复数：

   • Rust的标准库不直接提供有理数和复数类型，但可以使用第三方库（num）来实现。（use num::complex::Complex;）