【算法】区间DP （从记忆化搜索到递推DP）⭐

news2024/11/17 2:47:49

文章目录

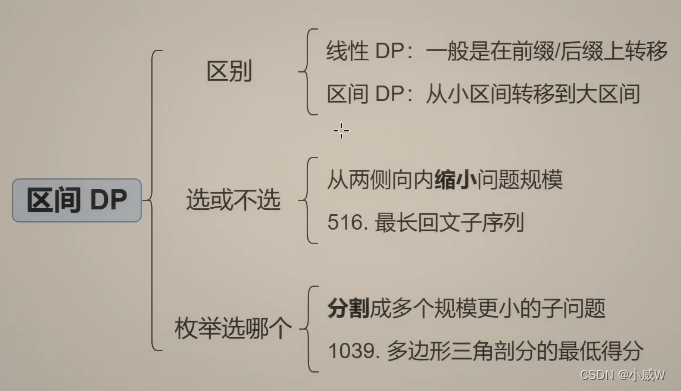
  • 前期知识
    • 516. 最长回文子序列
      • 思路1——转换问题：求 s 和反转后 s 的 LCS（最长公共子序列）
      • 思路2——区间DP：从两侧向内缩小问题规模
        • 补充：记忆化搜索代码
    • 1039. 多边形三角剖分的最低得分
      • 从记忆化搜索开始
      • 翻译成递推
  • 典型例题
  • 相关练习题目
    • 375. 猜数字大小 II https://leetcode.cn/problems/guess-number-higher-or-lower-ii/
      • 记忆化搜索
      • 递推dp
    • 1312. 让字符串成为回文串的最少插入次数 https://leetcode.cn/problems/minimum-insertion-steps-to-make-a-string-palindrome/
      • 记忆化搜索
      • 区间dp
      • 解法2：转换成最长回文子序列
    • 1771. 由子序列构造的最长回文串的长度 https://leetcode.cn/problems/maximize-palindrome-length-from-subsequences/
    • 1547. 切棍子的最小成本 https://leetcode.cn/problems/minimum-cost-to-cut-a-stick/
      • 记忆化搜索
      • 递推dp
    • 1000. 合并石头的最低成本 https://leetcode.cn/problems/minimum-cost-to-merge-stones/ ⭐⭐⭐⭐⭐
      • 前置知识——前缀和
      • 思路：寻找子问题
      • 记忆化搜索
        • 记忆化搜索的优化
      • DP递推

前期知识

在这里插入图片描述
通过本篇文章的学习，最重要的就是学会 记忆化搜索 的方法，
很多问题直接写 递推DP 会比较困难，但是寻找子问题，按照记忆化搜索的方式会比较简单。
之后还可以相对容易地将记忆化搜索的代码翻译成递推 DP。

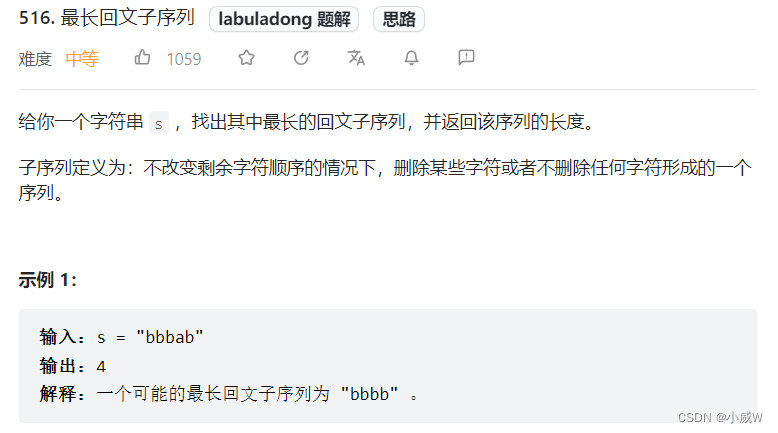
516. 最长回文子序列

516. 最长回文子序列
在这里插入图片描述

思路1——转换问题：求 s 和反转后 s 的 LCS（最长公共子序列）

因为回文子序列从前往后和从后往前是一样的，所以可以转换成求
s = eacbba
和
s_rev = abbace
的最长公共子序列的长度。最长公共子序列的方法参见：【算法】最长公共子序列&编辑距离

class Solution {
    public int longestPalindromeSubseq(String s) {
        int n = s.length();
        String s2 = new StringBuilder(s).reverse().toString();
        int[][] dp = new int[n + 1][n + 1];
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (s.charAt(i - 1) == s2.charAt(j - 1)) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] + 1);
                } else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        return dp[n][n];
    }
}

思路2——区间DP：从两侧向内缩小问题规模

在这里插入图片描述
这道题目相对简单一些，可以直接写出递推公式。

刚开始不确定 i 和 j 的枚举顺序，这时候看看状态转移方法看看它们是从哪里转移来的就好了。

class Solution {
    public int longestPalindromeSubseq(String s) {
        int n = s.length();
        // dp[i][j]表示从i~j的区间中，最长回文子序列的长度
        int[][] dp = new int[n][n];
        for (int i = n - 1; i >= 0; --i) {
            dp[i][i] = 1;   // dp数组初始化
            for (int j = i + 1; j < n; ++j) {
                if (s.charAt(i) == s.charAt(j)) {   
                    // i和j相同，可以选
                    dp[i][j] = Math.max(dp[i + 1][j - 1] + 2, dp[i][j]);
                } else {
                    // 不选i或者不选j
                    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);    
                }
            }
        }
        return dp[0][n - 1];
    }
}

补充：记忆化搜索代码

class Solution {
    int[][] memo;
    public int longestPalindromeSubseq(String s) {
        int n = s.length();
        this.memo = new int[n][n];
        return dfs(s.toCharArray(), 0, n - 1);
    }

    public int dfs(char[] s, int l, int r) {
        if (l > r) return 0;
        if (memo[l][r] != 0) return memo[l][r];
        if (l == r) return memo[l][r] = 1;
        if (s[l] == s[r]) memo[l][r] = Math.max(memo[l][r], dfs(s, l + 1, r - 1) + 2);
        else memo[l][r] = Math.max(dfs(s, l, r - 1), dfs(s, l + 1, r));
        return memo[l][r];
    }
}

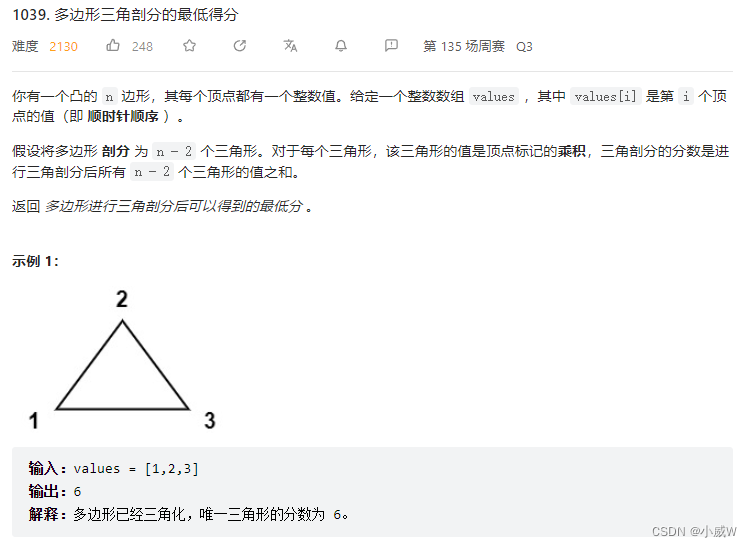
1039. 多边形三角剖分的最低得分

1039. 多边形三角剖分的最低得分
在这里插入图片描述

把这题当成经典例题，学习记忆化搜索的写法。

从记忆化搜索开始

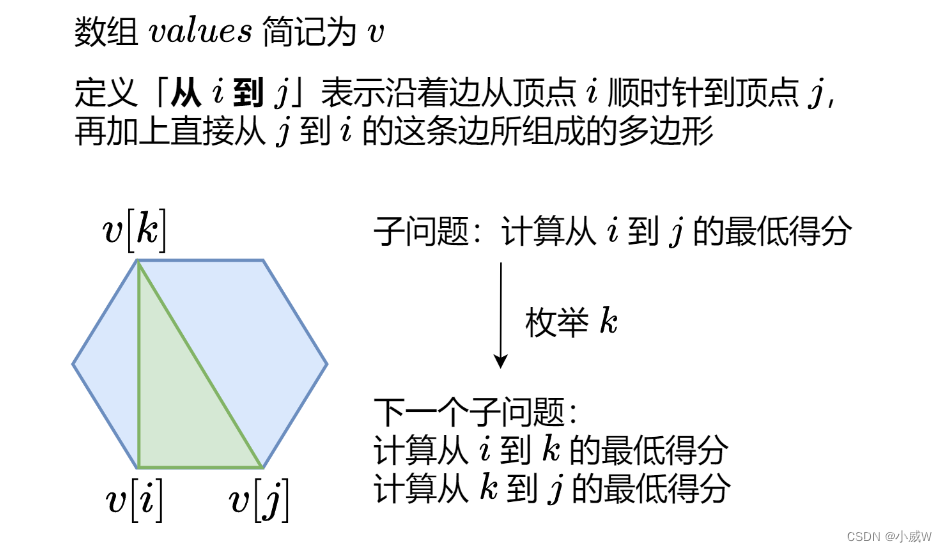
在这里插入图片描述
在这里插入图片描述

所谓记忆化搜索，就是用一个数组存一下各个 dfs 的结果，让 dfs 不会再重复计算。

class Solution {
    int[][] memo;

    public int minScoreTriangulation(int[] values) {
        int n = values.length;
        this.memo = new int[n][n];
        return dfs(values, 0, n - 1);
    }

    public int dfs(int[] values, int l, int r) {
        if (memo[l][r] != 0) return memo[l][r];
        else if (r == l + 1) memo[l][r] = 0;
        else {
            int res = Integer.MAX_VALUE;
            for (int i = l + 1; i < r; ++i) {
                res = Math.min(res, dfs(values, i, r) + dfs(values, l, i) + values[l] * values[i] * values[r]);
            }
            memo[l][r] = res;
        }
        return memo[l][r];
    }
}

翻译成递推

在这里插入图片描述

上图中说了，分不清枚举的顺序，就看状态转移的时候是从哪里转移过来的。

class Solution {
    public int minScoreTriangulation(int[] values) {
        int n = values.length;
        int[][] dp = new int[n][n];
        for (int i = n - 3; i >= 0; --i) {
            for (int j = i + 2; j < n; ++j) {
                dp[i][j] = Integer.MAX_VALUE;
                for (int k = i + 1; k < j; ++k) {
                    dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j] + values[i] * values[k] * values[j]);
                }
            }
        }
        return dp[0][n - 1];
    }
}

典型例题

相关练习题目

375. 猜数字大小 II https://leetcode.cn/problems/guess-number-higher-or-lower-ii/

https://leetcode.cn/problems/guess-number-higher-or-lower-ii/

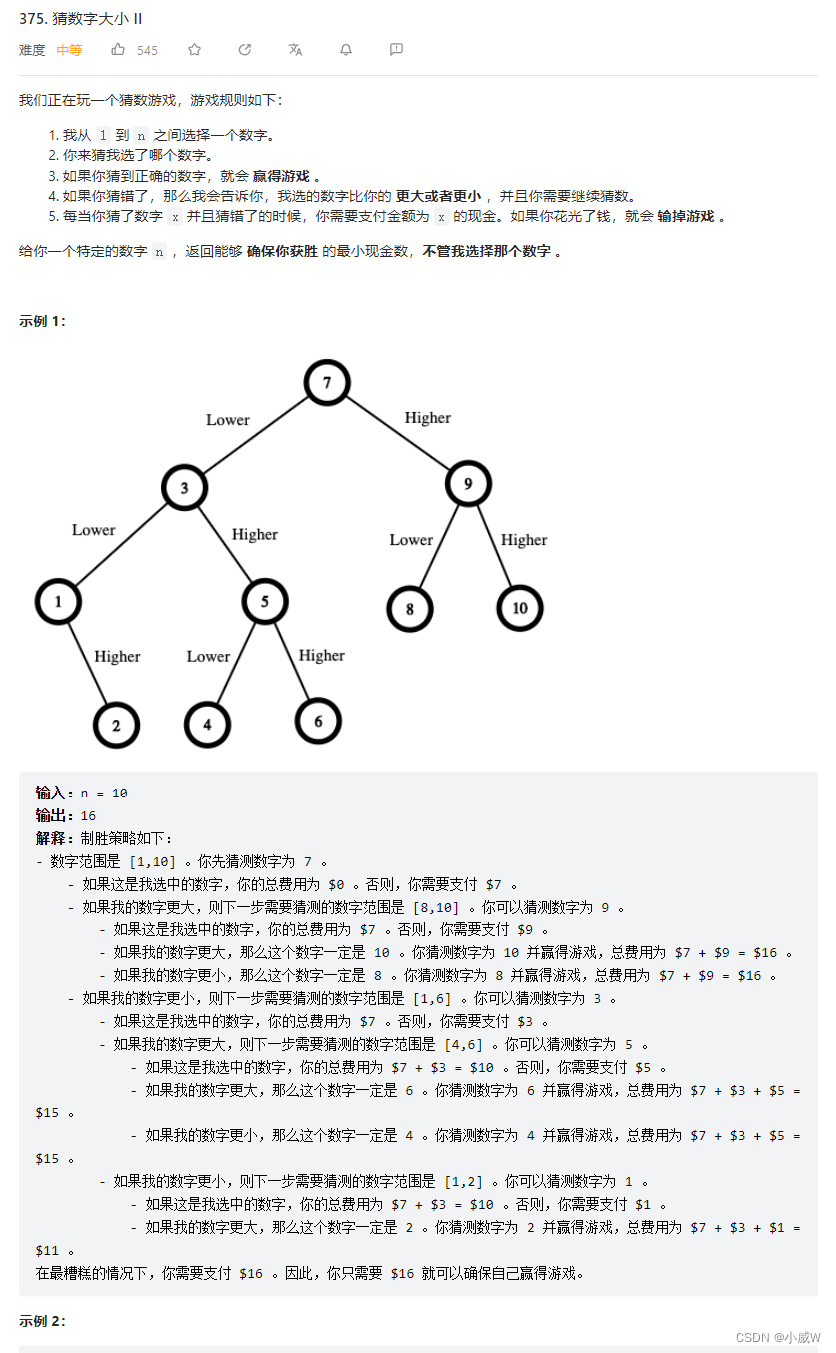
在这里插入图片描述

记忆化搜索

  1. 当只有一个数字需要被选择时，消耗是 0
  2. 当有两个数字需要被选择时，消耗是大的那一个，因为要保证游戏一定胜利
    在这里插入图片描述

res = Math.min(res, Math.max(dfs(l, i - 1), dfs(i + 1, r)) + i);

从记忆化搜索开始写，好写一些。

class Solution {
    int[][] memo;

    public int getMoneyAmount(int n) {
        memo = new int[n + 1][n + 1];
        return dfs(1, n);
    }

    public int dfs(int l, int r) {
        if (l >= r) return 0;
        if (memo[l][r] != 0) return memo[l][r];
        int res = Integer.MAX_VALUE;
        for (int i = l; i <= r; ++i) {
            res = Math.min(res, Math.max(dfs(l, i - 1), dfs(i + 1, r)) + i);
        }
        memo[l][r] = res;
        return res;
    }
}

递推dp

同样看递推的方向来判断枚举 i 和 j 的顺序。

class Solution {
    public int getMoneyAmount(int n) {
        int[][] dp = new int[n + 2][n + 2];
        for (int i = n; i >= 1; --i) {
            for (int j = i + 1; j <= n; ++j) {
                dp[i][j] = Integer.MAX_VALUE;
                for (int k = i; k <= j; ++k) {
                    dp[i][j] = Math.min(dp[i][j], k + Math.max(dp[i][k - 1], dp[k + 1][j]));
                }
            }
        }
        return dp[1][n];
    }
}

1312. 让字符串成为回文串的最少插入次数 https://leetcode.cn/problems/minimum-insertion-steps-to-make-a-string-palindrome/

https://leetcode.cn/problems/minimum-insertion-steps-to-make-a-string-palindrome/
在这里插入图片描述

  1. 当字符串的长度为 1 时，答案是0。
  2. 否则，当 s[i] != s[j] 时，需要增添一个元素 s[i] 或者 s[j]。答案是 dfs(s, l + 1, r) 和 dfs(s, l, r - 1) 之间的最小值 + 1。
  3. 当 s[i] == s[j] 时，答案是 dfs(s, l + 1, r - 1) ，因为这两个元素不需要考虑了。

记忆化搜索

class Solution {
    int[][] memo;

    public int minInsertions(String s) {
        int n = s.length();
        this.memo = new int[n][n];
        return dfs(s, 0, n - 1);
    }

    public int dfs(String s, int l, int r) {
        if (l >= r) return 0;
        if (memo[l][r] != 0) return memo[l][r];
        
        if (s.charAt(l) == s.charAt(r)) memo[l][r] = dfs(s, l + 1, r - 1);
        else memo[l][r] = 1 + Math.min(dfs(s, l + 1, r), dfs(s, l, r - 1));
        return memo[l][r];
    }
}

dfs 中第一句写的 if (l >= r) return 0; ，其实我也不知道在 dfs 的过程中 l 会不会 大于 r，但是无所谓，因为只有当 l < r 时我才想让函数接着往下走。
所以，何必写成 l == r 呢？不如宽松一点条件，省得万一 l 可能会大于 r。

区间dp

class Solution {
    public int minInsertions(String s) {
        int n = s.length();
        int[][] dp = new int[n][n];
        for (int i = n - 1; i >= 0; --i) {
            for (int j = i + 1; j < n; ++j) {
                if (s.charAt(i) == s.charAt(j)) dp[i][j] = dp[i + 1][j - 1];
                else dp[i][j] = 1 + Math.min(dp[i + 1][j], dp[i][j - 1]);
            }
        }
        return dp[0][n - 1];
    }
}

解法2：转换成最长回文子序列

考虑增加后的回文字符串，对称的两个字符不可能都是新增加的，要么其中一个是新增加的，要么就是都属于原字符串。如果只把两个都属于原字符串的那些字符作为子序列提出来（奇数长度的情况包含中间那个），他是一个回文子序列，并且是原字符串的回文子序列。并且有insertion step的数量就是原字符串长度 - 回文子序列的长度（要为那些本来只有一个的字符手动增加对称的字符）。

因此，一个增加字符使得原字符串变成回文的方案，对应着一个原字符串的回文子序列。并且，回文子序列越长，需要增加的字符越少。

从而变成找原字符串的最长回文子序列的问题。

class Solution {
    public int minInsertions(String s) {
        int n = s.length();
        // dp[i][j]表示从i~j之间的最长回文子序列的长度
        int[][] dp = new int[n][n];
        for (int i = n - 1; i >= 0; --i) {
            dp[i][i] = 1;
            for (int j = i + 1; j < n; ++j) {
                if (s.charAt(i) == s.charAt(j)) dp[i][j] = dp[i + 1][j - 1] + 2;
                else dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
            }
        }
        return n - dp[0][n - 1];
    }
}

1771. 由子序列构造的最长回文串的长度 https://leetcode.cn/problems/maximize-palindrome-length-from-subsequences/

https://leetcode.cn/problems/maximize-palindrome-length-from-subsequences/

在这里插入图片描述
这道题目本质上就是将 s1 和 s2 合并之后，求最长回文子序列，同时要求这个最长回文子序列的首元素在 s1 中，末尾元素在 s2 中。

class Solution {
    public int longestPalindrome(String word1, String word2) {
        String s = word1 + word2;
        int n = s.length(), n1 = word1.length(), ans = 0;
        int[][] dp = new int[n][n];
        for (int i = n - 1; i >= 0; --i) {
            dp[i][i] = 1;
            for (int j = i + 1; j < n; ++j) {
                if (s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                    if (i < n1 && j >= n1) ans = Math.max(ans, dp[i][j]);   // 需要在两个字符串上都选择
                }
                else dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
            } 
        }
        return ans;
    }
}

1547. 切棍子的最小成本 https://leetcode.cn/problems/minimum-cost-to-cut-a-stick/

https://leetcode.cn/problems/minimum-cost-to-cut-a-stick/

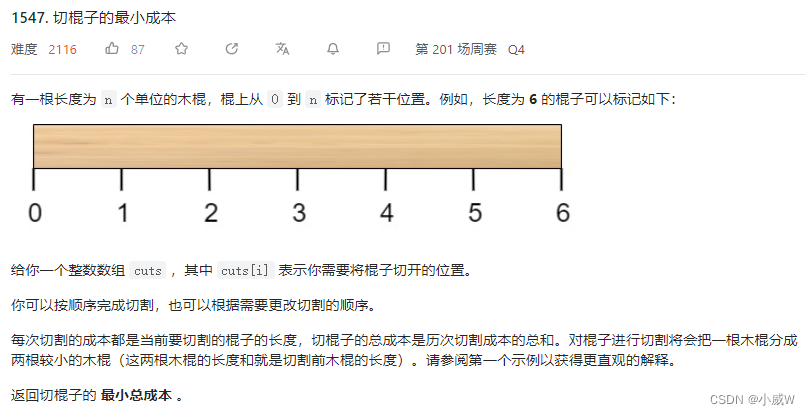
在这里插入图片描述
示例：
在这里插入图片描述

记忆化搜索

通过 dfs 求从 i ~ j 之间切割的最小花费。

class Solution {
    int[][] memo;   // 记忆数组

    public int minCost(int n, int[] cuts) {
        Arrays.sort(cuts);
        this.memo = new int[cuts.length][cuts.length];
        return dfs(cuts, 0, cuts.length - 1, 0, n);
    }

    public int dfs(int[] cuts, int l, int r, int start, int end) {
        if (l > r) return 0;
        if (memo[l][r] != 0) return memo[l][r];
        int res = Integer.MAX_VALUE;
        for (int i = l; i <= r; ++i) {
            res = Math.min(res, end - start + dfs(cuts, l, i - 1, start, cuts[i]) + dfs(cuts, i + 1, r, cuts[i], end));
        }
        memo[l][r] = res;
        return res;
    }
}

递推dp

先留给读者思考了。（实际上是自己不太会改
思考不出来可以看 https://leetcode.cn/problems/minimum-cost-to-cut-a-stick/solution/qie-gun-zi-de-zui-xiao-cheng-ben-by-leetcode-solut/

在这里插入代码片

1000. 合并石头的最低成本 https://leetcode.cn/problems/minimum-cost-to-merge-stones/ ⭐⭐⭐⭐⭐

https://leetcode.cn/problems/minimum-cost-to-merge-stones/

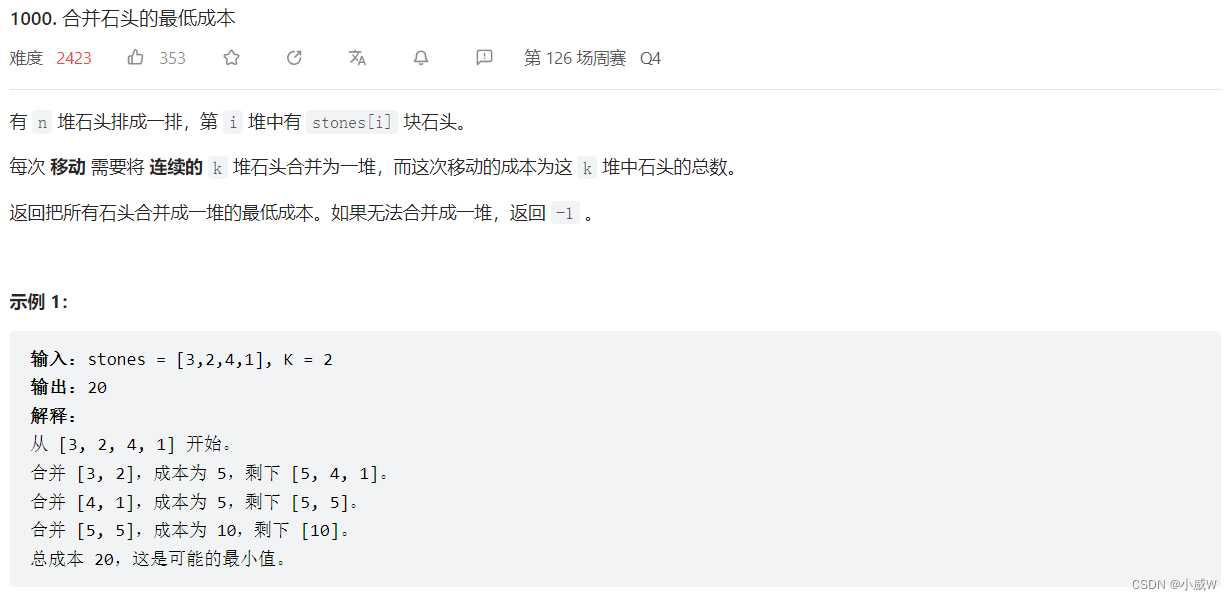
在这里插入图片描述

这道题目的难度还是很大的，但是学会之后收益颇丰。

前置知识——前缀和

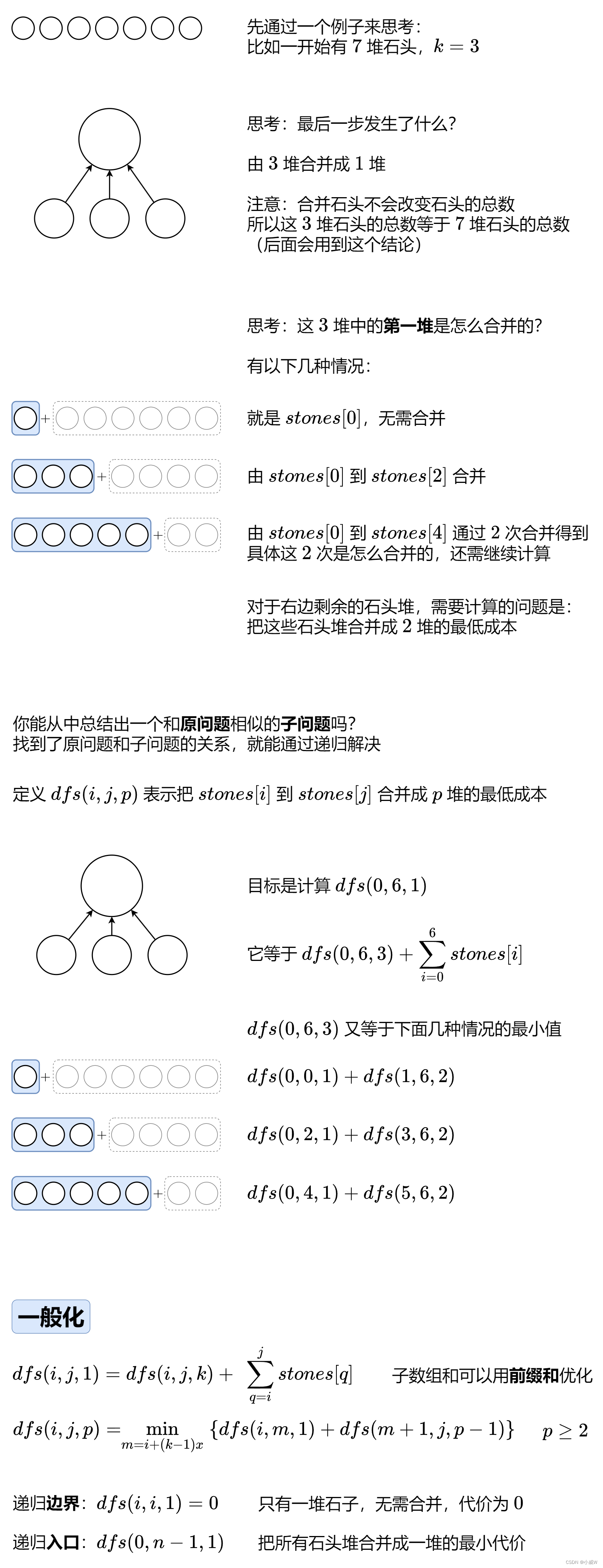
在这里插入图片描述

思路：寻找子问题

在这里插入图片描述

Q：什么时候输出-1呢？
A：从 n 堆变成 1 堆，需要减少 n - 1 堆，而每次合并都会减少 k - 1 堆，所以 n - 1 必须是 k - 1 的倍数。

记忆化搜索

将上面的思路转换成记忆化搜索。

class Solution {
    int[][][] memo;     // 记忆数组
    int[] s;            // 前缀和数组
    int k;

    public int mergeStones(int[] stones, int k) {
        int n = stones.length;
        if ((n - 1) % (k - 1) != 0) return -1;  // 返回-1
        this.s = new int[n + 1];
        // 计算前缀和数组
        for (int i = 0; i < n; ++i) {
            s[i + 1] = s[i] + stones[i];
        }
        this.k = k;
        this.memo = new int[n][n][k + 1];   // 表示从i~j合并成p堆的最低成本
        return dfs(0, n - 1, 1);    // 最后返回的是从0~n-1合并成1堆的最低成本
    }

    public int dfs(int l, int r, int p) {
        if (p == 1) return memo[l][r][p] = l == r? 0: dfs(l, r, k) + s[r + 1] - s[l];
        if (memo[l][r][p] != 0) return memo[l][r][p];   // 如果已经计算过了
        int res = Integer.MAX_VALUE;
        for (int i = l; i < r; i += k - 1) {
            res = Math.min(res, dfs(l, i, 1) + dfs(i + 1, r, p - 1));
        }
        return memo[l][r][p] = res;
    }
}

动态规划的时间复杂度 = 状态个数 × 单个状态的计算时间

时间复杂度： O ( N 3 ) O(N^3) O(N3)
空间复杂度： O ( N 2 K ) O(N^2K) O(N2K)

记忆化搜索的优化

在这里插入图片描述

class Solution {
    int[][] memo;     // 记忆数组
    int[] s;            // 前缀和数组
    int k;

    public int mergeStones(int[] stones, int k) {
        int n = stones.length;
        if ((n - 1) % (k - 1) != 0) return -1;  // 返回-1
        this.s = new int[n + 1];
        // 计算前缀和数组
        for (int i = 0; i < n; ++i) {
            s[i + 1] = s[i] + stones[i];
        }
        this.k = k;
        this.memo = new int[n][n];   // 表示从i~j合并成1堆的最低成本
        return dfs(0, n - 1);    // 最后返回的是从0~n-1合并成1堆的最低成本
    }

    public int dfs(int l, int r) {
        if (l == r) return 0;                   // 如果已经是一堆了
        if (memo[l][r] != 0) return memo[l][r];   // 如果已经计算过了
        int res = Integer.MAX_VALUE;
        for (int i = l; i < r; i += k - 1) {
            res = Math.min(res, dfs(l, i) + dfs(i + 1, r));
        }
        if ((r - l) % (k - 1) == 0) {           // 如果可以合并成一堆
            res += s[r + 1] - s[l];
        }
        return memo[l][r] = res;
    }
}

DP递推

直接写出来递推还是挺难的，但是可以从记忆化搜索的代码 1：1 翻译成递推 DP。

class Solution {
    public int mergeStones(int[] stones, int k) {
        int n = stones.length;
        if ((n - 1) % (k - 1) != 0) return -1;  // 返回-1
        // 计算前缀和数组
        int[] s = new int[n + 1];
        for (int i = 0; i < n; ++i) {
            s[i + 1] = s[i] + stones[i];
        }

        int[][] dp = new int[n][n];
        for (int i = n - 1; i >= 0; --i) {
            for (int j = i + 1; j < n; ++j) {
                dp[i][j] = Integer.MAX_VALUE / 2;
                for (int m = i; m < j; m += k - 1) {
                    dp[i][j] = Math.min(dp[i][j], dp[i][m] + dp[m + 1][j]);
                }
                if ((j - i) % (k - 1) == 0) dp[i][j] += s[j + 1] - s[i];
            }
        }
        return dp[0][n - 1];
    }
}

在这里插入图片描述
还是经典的那句话，不知道枚举的顺序，就看状态从哪里转移过来。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/705554.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

改造3dmax的快捷键自定义3dmax快捷键

改造3dmax的快捷键自定义3dmax快捷键

快捷键需要整体规划&#xff0c;不然太乱了&#xff0c;不要担心你的自定义快捷键破坏了系统原有的快捷键&#xff0c;或者和原有的某些快捷键冲突&#xff0c;如果那些被系统定义的快捷键所对应的功能指令你都不知道他们是干什么用的&#xff0c;你要他们有什么用。还不如来得…
阅读更多...
Rust 基础入门 ——数值类型

Rust 基础入门 ——数值类型

数值类型 概述 数值类型 这里重点在于一些特殊的书写方式的格式&#xff0c;和几种特殊类型。除此以外&#xff0c;还包括一些常见的类型处理方式&#xff08;这之中包括了一些问题处理和Rust 特有内容&#xff09;。 细分之下为&#xff1a; 整数类型 重点问题&#xff1a…
阅读更多...
基于PyQt5的图形化界面开发——天气应用

基于PyQt5的图形化界面开发——天气应用

目录 0. 前言1. 注册心知天气2. 代码实现3. 其他PyQt5文章 0. 前言 本节使用PyQt5开发天气应用程序实现以下功能&#xff1a; 通过调用天气API获取实时天气数据&#xff0c;并在应用程序中显示当前城市的温度、天气状况、风速等信息。 操作系统&#xff1a;Windows10 专业版…
阅读更多...
关于 3.0 和 2.0 的数据文件差异以及性能优化思路

关于 3.0 和 2.0 的数据文件差异以及性能优化思路

如果需要对数据库性能优化&#xff0c;了解数据文件的存储方式和工作原理是必要的。 对于时序数据库&#xff08;Time Series Database&#xff09; TDengine 来说&#xff0c;在 2.x 版本中时序数据的保留策略是由keep和days这两个参数把控的。&#xff08;详情可见&#xff…
阅读更多...
云原生——Kubenetes基础

云原生——Kubenetes基础

❄️作者介绍&#xff1a;奇妙的大歪❄️ &#x1f380;个人名言&#xff1a;但行前路&#xff0c;不负韶华&#xff01;&#x1f380; &#x1f43d;个人简介&#xff1a;云计算网络运维专业人员&#x1f43d; 目录 一.什么是Kubernetes&#xff1f; 二.为什么你需要 Kubern…
阅读更多...
markdown数学公式总结

markdown数学公式总结

行内与独行 行内公式&#xff1a;将公式插入到本行内&#xff0c;符号&#xff1a; 公式内容 公式内容 公式内容&#xff0c;如&#xff1a; x y z xyz xyz 独行公式&#xff1a;将公式插入到新的一行内&#xff0c;并且居中&#xff0c;符号&#xff1a; 公式内容 公式内容 公…
阅读更多...
RISC-V IDE MRS使用笔记(十)：嵌入式编程开发技巧汇总

RISC-V IDE MRS使用笔记(十)：嵌入式编程开发技巧汇总

RISC-V IDE MRS使用笔记(十)&#xff1a;嵌入式编程开发技巧汇总 MRS常见嵌入式开发技巧: Q1&#xff1a;如何修改程序编译生成库&#xff1f; A1&#xff1a;在工具栏中点击活动工程的编译配置按钮&#xff0c;在Build Artifact的Tab页面指定目标类型&#xff0c;选中为Stat…
阅读更多...
uniapp仿浙北惠生活微信小程序

uniapp仿浙北惠生活微信小程序

最近给公司写了一个内部微信小程序&#xff0c;功能比较简单&#xff0c;之前是用微信小程序原声写的&#xff0c;一遍看文档一边写&#xff0c;js&#xff0c;wxml&#xff0c;wxcc&#xff0c;json分在不同文件的写法很不习惯&#xff0c;于是花了两天用uniapp重写了一遍&…
阅读更多...
思维导图对我生活以及工作的帮助（用户投稿）

思维导图对我生活以及工作的帮助（用户投稿）

作为一名白领&#xff0c;我每天都面临着各种各样的工作和生活压力。 为了更好地应对这些挑战&#xff0c;我开始尝试使用思维导图来帮助自己更好地组织和管理各种信息和任务。其中一款非常优秀的软件就是ProcessOn思维导图&#xff0c;它为我的工作和生活带来了很多便利和帮助…
阅读更多...
Spring Boot|启动图案修改ASCII字符画

Spring Boot|启动图案修改ASCII字符画

效果图 实现 在项目目录的resources文件夹中新建一个banner.txt&#xff0c;将内容放入即可&#xff1a; // _ooOoo_ // // o8888888o // // …
阅读更多...
华为ENSP配置无线AC-网关模式

华为ENSP配置无线AC-网关模式

1、配置交换机以及AC的接口为trunk 交换机 vlan b 10 20 # interface GigabitEthernet0/0/1port link-type trunkport trunk allow-pass vlan 10 20 # # interface GigabitEthernet0/0/2port link-type trunkport trunk pvid vlan 10port trunk allow-pass vlan 10 20 # …
阅读更多...
Linux系统安装QQ最新版 2023-06-30

Linux系统安装QQ最新版 2023-06-30

腾讯在2023-05-30更新了linux版的qq&#xff0c;这次界面终于不再复古&#xff0c;好看多了。 安装步骤&#xff1a; 1.进入官网&#xff0c;寻找合适的安装包下载 https://im.qq.com/linuxqq/index.shtml 选择跟自己计算机匹配的版本&#xff0c;一般都是X86&#xff0c;如…
阅读更多...
JAVA-编程基础-05-方法的定义、调用、重载

JAVA-编程基础-05-方法的定义、调用、重载

Lison <dreamlison163.com>, v1.0.0, 2023.03.22 JAVA-编程基础-05-方法的定义、调用、重载 文章目录 JAVA-编程基础-05-方法的定义、调用、重载方法的概念什么是方法 方法的定义和调用无参数方法定义和调用方法调用过程图解 带参数方法的定义和调用带返回值方法的定义和…
阅读更多...
Ureport 多数据集合关联显示

Ureport 多数据集合关联显示

ureport 使用较少&#xff0c;目前单位这边有项目正好使用到了&#xff0c;也遇到不少坑&#xff0c;和其他报表稍微有些不同&#xff0c;在这里记录一下&#xff0c;为大家排一下坑 目前需求是要求数据以这样显示 1、创建数据源 1.1 B2、C1、D2 、C4、C2 各使用了不同的数据…
阅读更多...
chatGPT流式回复是怎么实现的

chatGPT流式回复是怎么实现的

chatGPT流式回复是怎么实现的 先说结论&#xff1a; chatGPT的流式回复用的就是HTTP请求方案中的server-send-event流式接口&#xff0c;也就是服务端向客户端推流数据。 那eventStream流式接口怎么实现呢&#xff0c;下面就进入正题&#xff01; 文章目录 chatGPT流式回复…
阅读更多...
UE5ControlRig脚部IK匹配地面（FootIK）的简易实现

UE5ControlRig脚部IK匹配地面（FootIK）的简易实现

UE的Foot IK可以有多套方案&#xff0c;老的有动画蓝图中用TwoBoneIK&#xff0c;新的做法有ControlRig的BasicIK、FullBodyIK。博主针对FootIK做一个简单的验证&#xff0c;因此使用ControlRigTwoBoneIK的做法&#xff0c;并做一下记录&#xff0c;之前做过UE FootIK的大佬可以…
阅读更多...
小白到运维工程师自学之路 第四十四集 （mariadb高可用集群故障转移）

小白到运维工程师自学之路 第四十四集 （mariadb高可用集群故障转移）

一、概述 故障转移是指在集群中某个节点发生故障时&#xff0c;自动将服务转移到其他正常节点上的 过程。在MariaDB高可用集群中&#xff0c;通常使用主从复制的方式来实现故障转移。其中一个 节点被指定为主节点&#xff0c;负责处理所有的写操作和部分读操作&#xff0c;其…
阅读更多...
通过无模型多代理强化学习掌握Stratego游戏

通过无模型多代理强化学习掌握Stratego游戏

Stratego是一款流行的双人不完美信息棋盘游戏。由于其复杂性源于其巨大的游戏树、在不完善的信息下进行决策以及一开始的分段部署阶段&#xff0c;Stratego对人工智能&#xff08;AI&#xff09;构成了挑战。以前的计算机程序充其量只在业余水平上运行。 Perolat等人引入了一种…
阅读更多...
Crontab的sendmail邮件发送引发磁盘问题

Crontab的sendmail邮件发送引发磁盘问题

一.背景 大清早的收到一台服务器的内存占用高达98%的钉钉告警。 回想了一下&#xff0c;这台服务器没跑什么业务啊&#xff0c;咋从凌晨1点就开始告警呢? 赶紧登录服务器&#xff0c;top 按照内存倒序一下&#xff0c;没发现占用特别大的进程。内存监控图如下: 但是发现了很…
阅读更多...
Windows环境本地部署Oracle11g r2实操手册

Windows环境本地部署Oracle11g r2实操手册

前言&#xff1a;一直在做其他测试&#xff0c;貌似都忘了Windows环境oracle安装&#xff0c;这是一个很早很早的安装记录了&#xff0c;放上来做个备录给到大家参考。 环境&#xff1a; &#xff08;都是常规系统及工具&#xff0c;官网度娘搜索即可下载测试学习&#xff09;…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023