RS-FAIRFRS: COMMUNICATION EFFICIENT FAIR FEDERATED RECOMMENDER SYSTEM
Anonymous authors
Paper under double-blind review
communication efficient fair federated recommender system
ICLR 2023
1. What does literature study?
- 结合随机抽样和确定每轮通信中要抽样的客户端数量以保持模型在FRS中的准确性;训练本地客户端建立公平的全局模型,以减少客户端层面的人口偏见。
2. What’s the innovation?
1. Past shortcomings
- 监督学习算法通过在训练损失中添加公平约束来减轻群体偏见,这需要与服务器共享受保护的属性
2.Innovation:
- 提出的基于随机抽样的公平联邦推荐系统无需分享其受保护的属性。
- 提供了客户端采样复杂度界限提高了通信成本。
- 在两个数据集(ML-1M,ML-100K)和不同的敏感特征(年龄和性别)中证明RS-FAIRFRS有助于降低通信成本和人口统计偏差,提高了模型的准确性。
3. What was the methodology?

利用FedRec作为基础模型,使用矩阵分解识别潜在特征向量。最小化损失函数:
L
M
F
=
∑
u
∈
[
n
]
∑
i
∈
[
m
]
p
u
i
(
r
u
i
−
U
u
⋅
V
i
T
)
2
+
λ
r
(
∥
V
i
∥
2
+
∥
U
u
∥
2
)
\mathcal{L}^{\mathcal{M F}}=\sum_{u \in[n]} \sum_{i \in[m]} p_{u i}\left(r_{u i}-U_u \cdot V_i^T\right)^2+\lambda^r\left(\left\|V_i\right\|^2+\left\|U_u\right\|^2\right)
LMF=∑u∈[n]∑i∈[m]pui(rui−Uu⋅ViT)2+λr(∥Vi∥2+∥Uu∥2)
1.随机采样
利用霍夫丁约束支持不替换的抽样,随机均匀采样(无替换,不重复)将包含来自每个集群的大致相等数量的客户端。
采样
C
T
C^{\mathcal{T}}
CT个客户端的平均项目向量:
V
ˉ
i
τ
=
1
n
τ
∑
i
∈
C
τ
V
i
\bar{V}_i^\tau=\frac{1}{n \tau} \sum_{i \in C^\tau} V_i
Vˉiτ=nτ1∑i∈CτVi,总的
n
n
n个客户端的平均项目向量:
V
ˉ
i
n
=
1
n
∑
i
=
1
n
V
i
\bar{V}_i^n=\frac{1}{n} \textstyle\sum_{i=1}^n V_i
Vˉin=n1∑i=1nVi。使样本和整个训练集预测评分的期望相等
E
[
U
u
T
V
ˉ
i
τ
]
=
E
[
U
u
T
V
ˉ
i
n
]
\mathbb{E}[U_u^T\bar{V}_i^\tau]=\mathbb{E}[U_u^T\bar{V}_i^n]
E[UuTVˉiτ]=E[UuTVˉin]。
2.双公平更新
精度奇偶性
L
a
p
=
1
∣
g
∣
∑
u
∈
g
1
∣
I
u
∣
∑
I
∈
I
u
(
r
^
u
i
−
r
u
i
)
2
−
1
∣
¬
g
∣
∑
u
∈
¬
g
1
∣
I
u
∣
∑
I
∈
I
u
(
r
^
u
i
−
r
u
i
)
2
\mathcal{L}^{a p}=\frac{1}{|g|} \sum_{u \in g} \frac{1}{\left|I_u\right|} \sum_{I \in I_u}\left(\hat{r}_{u i}-r_{u i}\right)^2-\frac{1}{|\neg g|} \sum_{u \in \neg g} \frac{1}{\left|I_u\right|} \sum_{I \in I_u}\left(\hat{r}_{u i}-r_{u i}\right)^2
Lap=∣g∣1u∈g∑∣Iu∣1I∈Iu∑(r^ui−rui)2−∣¬g∣1u∈¬g∑∣Iu∣1I∈Iu∑(r^ui−rui)2,表示两个群体之间的差异。对于模型
θ
{\theta}
θ和
θ
ˉ
\bar{\theta}
θˉ,如果
L
a
p
(
θ
)
<
L
a
p
(
θ
ˉ
)
\mathcal{L}^{a p}({\theta})<\mathcal{L}^{a p}(\bar{\theta})
Lap(θ)<Lap(θˉ),则
θ
{\theta}
θ更公平。
服务器端20%的客户端数据用来评估公平损失:
min
U
,
V
L
M
F
+
λ
f
L
a
p
\min\limits_{U,V}\mathcal{L}^{MF}+\lambda^f\mathcal{L}^{ap}
U,VminLMF+λfLap以获得
V
f
a
i
r
V_{fair}
Vfair发给客户端。
客户端从服务器下载
V
f
a
i
r
V_{fair}
Vfair和
V
i
V_{i}
Vi;公平目标函数为:
min
U
,
V
L
M
F
+
η
(
∣
∣
V
f
a
i
r
−
V
i
∣
∣
2
)
\min\limits_{U,V}\mathcal{L}^{MF}+\eta(||V_{fair}-V_i||^2)
U,VminLMF+η(∣∣Vfair−Vi∣∣2)
4. What are the conclusions?
- 结论:
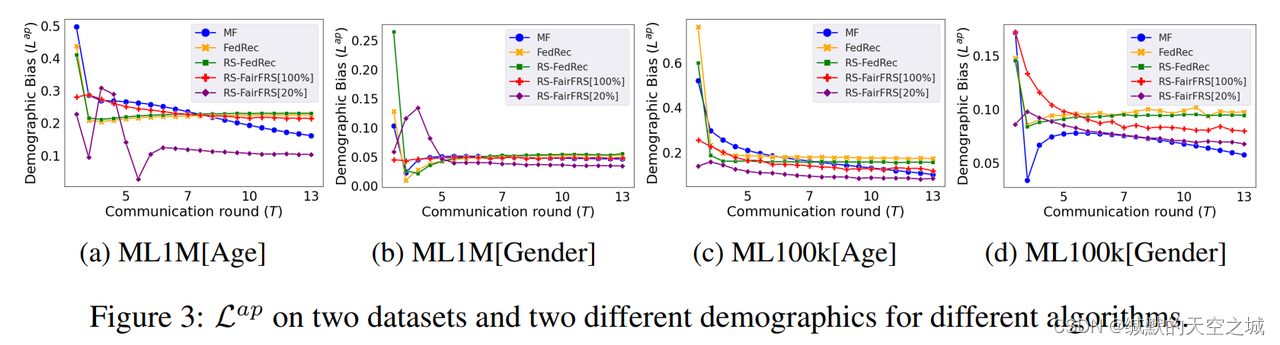
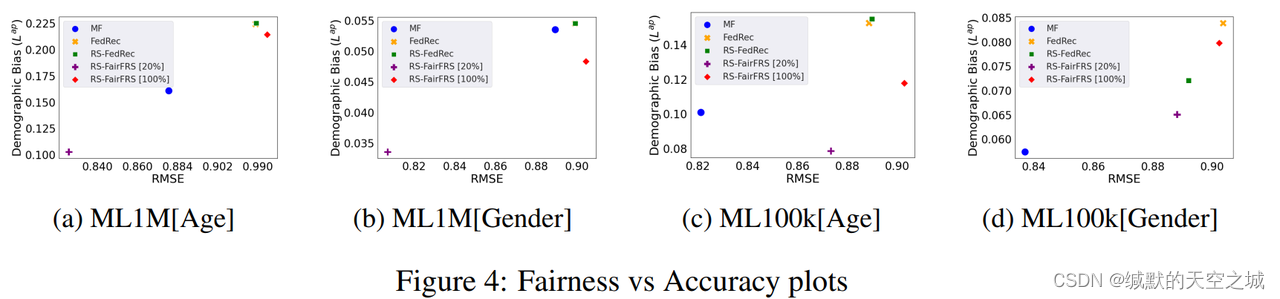
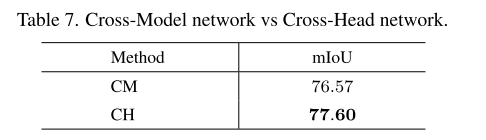
经过实验客户端抽样比率为 T = 35 % {\mathcal{T}}=35\% T=35%作为理想值;>18和男性群体数量多可以获得更低的损失;RS-FairFRS可以实现公平性。
5. others
男多女少,平均抽样
-
我们提出了一种具有两个阶段的双公平向量更新技术。在阶段1中,服务器聚合接收到的项目向量,并对其进行训练,使其在一小部分数据上公平。在第2阶段,客户端将本地误差降至最低,并学习更接近全局公平项目向量的项目向量。
-
利用FedRec作为基础模型,客户端上传项目梯度,从服务器下载项目向量。
(1)FRS中的人口统计学偏差问题,量化为不同组间平均错误率差异。
(2)给出了FRS的样本复杂度边界。 -
集中式RS领域的公平性:
(1)Sirui Yao and Bert Huang. Beyond parity: Fairness objectives for collaborative filtering. Advances in neural information processing systems, 30, 2017.
RecBole-FairRec-Optimized/focf.py at 5c88cb8c2f2586febe6bff8832d7bdc326e8392b · Keyvantajfar/RecBole
RecBole-FairRec/focf.py at 08a7f4cf330477bc4e755749df7dda826e96384a · TangJiakai/RecBole-FairRec
(2) Yunqi Li, Hanxiong Chen, Zuohui Fu, Yingqiang Ge, and Yongfeng Zhang. User-oriented fairness in recommendation. In Proceedings of the Web Conference 2021, pp. 624–632, 2021.
https://github.com/rutgerswiselab/user-fairness