1、权重衰退

1. 基础概念

实际上，限制特征的数量是缓解过拟合的一种常用技术。然而，简单地丢弃特征对这项工作来说可能过于生硬。我们继续思考多项式回归的例子，考虑高维输入可能发生的情况。多项式对多变量数据的自然扩展称为单项式（monomials），也可以说是变量幂的乘积。单项式的阶数是幂的和。

例如，$x_1^2{x}_2$和$x_3{x}_5^2$都是3次单项式。注意，随着阶数$d$的增长，带有阶数$d$的项数迅速增加。 给定$k$个变量，阶数为$d$的项的个数为$\left(\genfrac{}{}{0ex}{}{k-1+d}{k-1}\right)$，即$C_{k-1+d}^{k-1}=\frac{(k-1+d)!}{(d)!(k-1)!}$。因此即使是阶数上的微小变化，比如从$2$到$3$，也会显著增加我们模型的复杂性。仅仅通过简单的限制特征数量（在多项式回归中体现为限制阶数），可能仍然使模型在过简单和过复杂中徘徊，我们需要一个更细粒度的工具来调整函数的复杂性，使其达到一个合适的平衡位置。

我们已经描述了$L_2$范数和$L_1$范数，它们是更为一般的$L_p$范数的特殊情况。在训练参数化机器学习模型时，权重衰减（weight decay）是最广泛使用的正则化的技术之一，它通常也被称为$L_2$正则化。

这项技术通过函数与零的距离来衡量函数的复杂度，因为在所有函数$f$中，函数$f=0$（所有输入都得到值$0$）在某种意义上是最简单的。但是我们应该如何精确地测量一个函数和零之间的距离呢？没有一个正确的答案。事实上，函数分析和巴拿赫空间理论的研究，都在致力于回答这个问题。

一种简单的方法是通过线性函数$f(\mathbf{x})={\mathbf{w}}^{\top }\mathbf{x}$中的权重向量的某个范数来度量其复杂性，例如$\Vert \mathbf{w}{\Vert }^2$。要保证权重向量比较小，最常用方法是将其范数作为惩罚项加到最小化损失的问题中。将原来的训练目标 最小化训练标签上的预测损失，调整为最小化预测损失和惩罚项之和。 现在，如果我们的权重向量增长的太大，我们的学习算法可能会更集中于最小化权重范数$\Vert \mathbf{w}{\Vert }^2$。这正是我们想要的。让我们回顾一下性回归例子。我们的损失由下式给出：

$$L(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right)}^2.$$

回想一下，${\mathbf{x}}^{(i)}$是样本$i$的特征，$y^{(i)}$是样本$i$的标签，$(\mathbf{w},b)$是权重和偏置参数。为了惩罚权重向量的大小，

我们必须以某种方式在损失函数中添加$\Vert \mathbf{w}{\Vert }^2$，但是模型应该如何平衡这个新的额外惩罚的损失？实际上，我们通过正则化常数$\lambda$来描述这种权衡，这是一个非负超参数，我们使用验证数据拟合：

$$L(\mathbf{w},b)+\frac{\lambda }{2}\Vert \mathbf{w}{\Vert }^2,$$

对于$\lambda =0$，我们恢复了原来的损失函数。对于$\lambda >0$，我们限制$\Vert \mathbf{w}\Vert$的大小。

这里我们仍然除以$2$：当我们取一个二次函数的导数时，$2$和$1/2$会抵消，以确保更新表达式看起来既漂亮又简单。为什么在这里我们使用平方范数而不是标准范数（即欧几里得距离）？我们这样做是为了便于计算。 通过平方$L_2$范数，我们去掉平方根，留下权重向量每个分量的平方和。这使得惩罚的导数很容易计算：导数的和等于和的导数。

此外，为什么我们首先使用$L_2$范数，而不是$L_1$范数。事实上，这个选择在整个统计领域中都是有效的和受欢迎的。$L_2$正则化线性模型构成经典的岭回归（ridge regression）算法，$L_1$正则化线性回归是统计学中类似的基本模型，通常被称为套索回归（lasso regression）。 使用$L_2$范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。 在实践中，这可能使它们对单个变量中的观测误差更为稳定。相比之下，$L_1$惩罚会导致模型将权重集中在一小部分特征上，而将其他权重清除为零。 这称为特征选择（feature selection），这可能是其他场景下需要的。

$L_2$正则化回归的小批量随机梯度下降更新如下式：

$$\begin{array}{rl}\mathbf{w}& \leftarrow \left(1-\eta \lambda \right)\mathbf{w}-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{\mathbf{x}}^{(i)}\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right).\end{array}$$

根据之前章节所讲的，我们根据估计值与观测值之间的差异来更新$\mathbf{w}$。然而，我们同时也在试图将$\mathbf{w}$的大小缩小到零。这就是为什么这种方法有时被称为权重衰减。我们仅考虑惩罚项，优化算法在训练的每一步衰减权重。与特征选择相比，权重衰减为我们提供了一种连续的机制来调整函数的复杂度。较小的$\lambda$值对应较少约束的$\mathbf{w}$，而较大的$\lambda$值对$\mathbf{w}$的约束更大。

是否对相应的偏置$b^2$进行惩罚在不同的实践中会有所不同，在神经网络的不同层中也会有所不同。通常，网络输出层的偏置项不会被正则化。

2. 代码演示

（1）生成数据

首先，我们[像以前一样生成一些数据]，生成公式如下：

$$y=0.05+\sum _{i=1}^{d}0.01x_i+ϵ\text{ where }ϵ\sim \mathcal{N}(0,0.01^2).$$

我们选择标签是关于输入的线性函数。标签同时被均值为0，标准差为0.01高斯噪声破坏。
为了使过拟合的效果更加明显，我们可以将问题的维数增加到$d=200$，并使用一个只包含20个样本的小训练集。

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

（2）初始化模型参数

def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]

（3）定义惩罚项

def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2
def l1_penalty(w):
    return torch.sum(torch.abs(w))

（4）训练

def train(lambd):
    w, b = init_params()
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
    num_epochs, lr = 100, 0.003
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 增加了L2范数惩罚项，
            # 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
            l = loss(net(X), y) + lambd * l2_penalty(w)
            # l = loss(net(X), y) + lambd * l1_penalty(w)
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数是：', torch.norm(w).item())
 

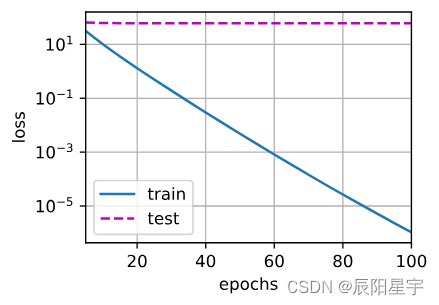
不适用权重衰退

train(lambd=0)   

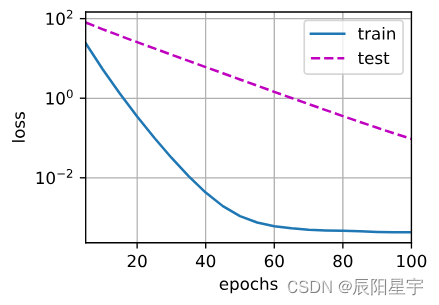
使用权重衰退L2

train(lambd=3)

使用权重衰退L1

train(lambd=3)

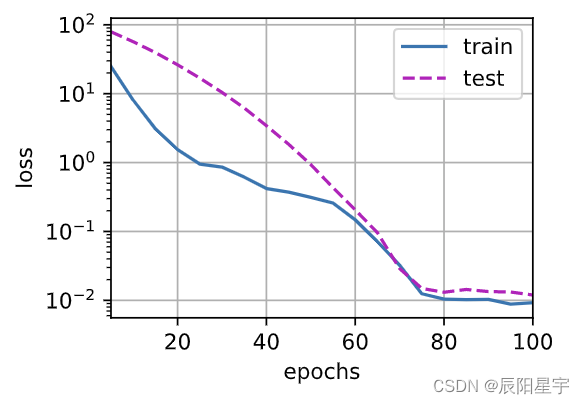
参考文章：4.5. 权重衰减

2、丢弃法

1. 扰动性

我们介绍了通过惩罚权重的$L_2$范数来正则化统计模型的经典方法。 在概率角度看，我们可以通过以下论证来证明这一技术的合理性： 我们已经假设了一个先验，即权重的值取自均值为0的高斯分布。 更直观的是，我们希望模型深度挖掘特征，即将其权重分散到许多特征中， 而不是过于依赖少数潜在的虚假关联。

在探究泛化性之前，我们先来定义一下什么是一个“好”的预测模型？我们期待“好”的预测模型能在未知的数据上有很好的表现：经典泛化理论认为，为了缩小训练和测试性能之间的差距，应该以简单的模型为目标。简单性以较小维度的形式展现，我们在讨论线性模型的单项式函数时探讨了这一点。 此外，正如我们在中讨论权重衰减（$L_2$正则化）时看到的那样，参数的范数也代表了一种有用的简单性度量。

简单性的另一个角度是平滑性，即函数不应该对其输入的微小变化敏感。例如，当我们对图像进行分类时，我们预计向像素添加一些随机噪声应该是基本无影响的。1995年，克里斯托弗·毕晓普证明了具有输入噪声的训练等价于Tikhonov正则化 :cite:Bishop.1995。这项工作用数学证实了**“要求函数光滑”和“要求函数对输入的随机噪声具有适应性”之间的联系**。

然后在2014年，斯里瓦斯塔瓦等人 :cite:Srivastava.Hinton.Krizhevsky.ea.2014就如何将毕晓普的想法应用于网络的内部层提出了一个想法：在训练过程中，他们建议在计算后续层之前向网络的每一层注入噪声。因为当训练一个有多层的深层网络时，注入噪声只会在输入-输出映射上增强平滑性。

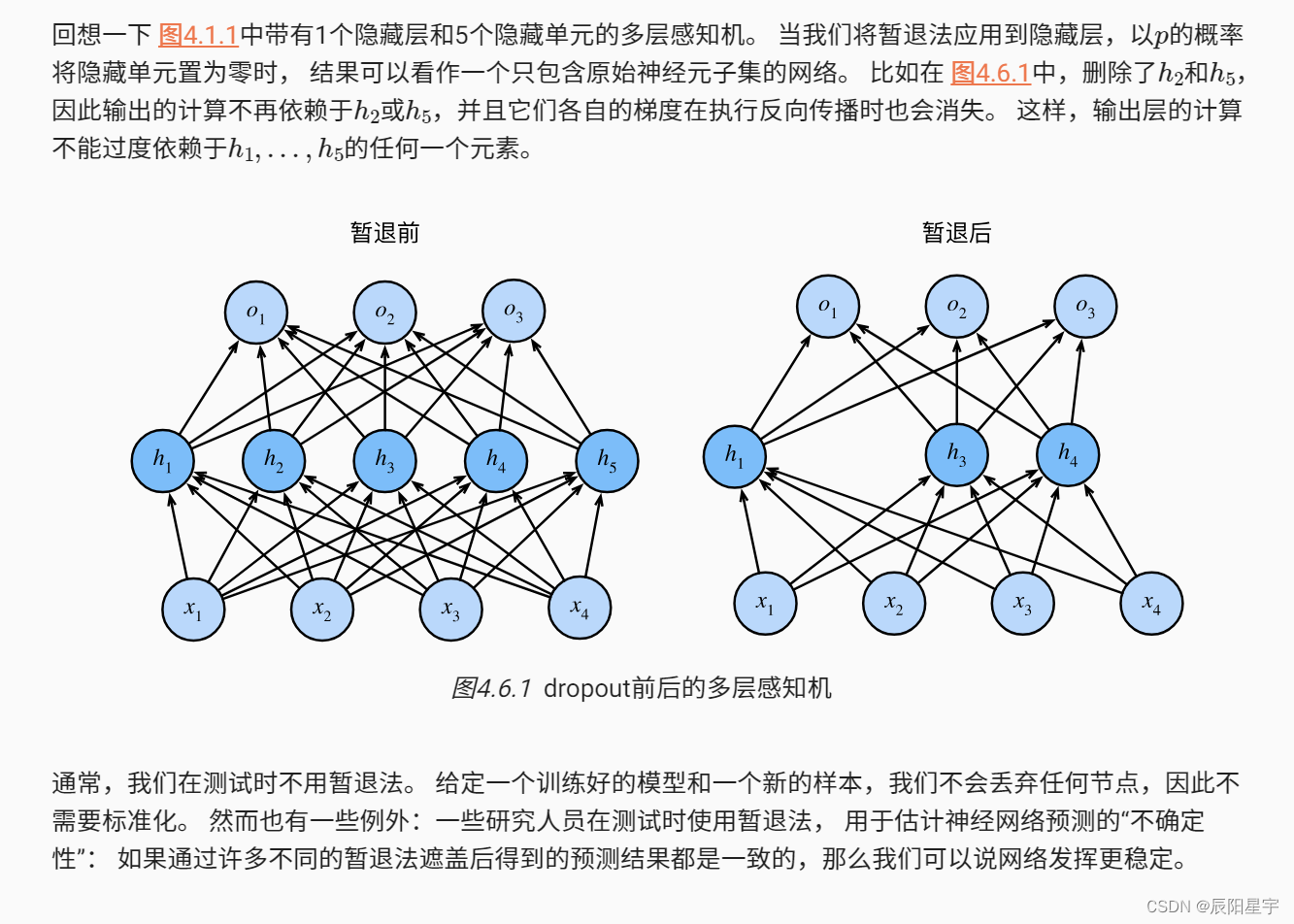
这个想法被称为暂退法（dropout）。暂退法在前向传播过程中，计算每一内部层的同时注入噪声，这已经成为训练神经网络的常用技术。这种方法之所以被称为暂退法，因为我们从表面上看是在训练过程中丢弃（drop out）一些神经元。在整个训练过程的每一次迭代中，标准暂退法包括在计算下一层之前将当前层中的一些节点置零。

需要说明的是，暂退法的原始论文提到了一个关于有性繁殖的类比：神经网络过拟合与每一层都依赖于前一层激活值相关，称这种情况为“共适应性”。作者认为，暂退法会破坏共适应性，就像有性生殖会破坏共适应的基因一样。

那么关键的挑战就是如何注入这种噪声。一种想法是以一种无偏向（unbiased）的方式注入噪声。
这样在固定住其他层时，每一层的期望值等于没有噪音时的值。

在毕晓普的工作中，他将高斯噪声添加到线性模型的输入中。在每次训练迭代中，他将从均值为零的分布$ϵ\sim \mathcal{N}(0,{\sigma }^2)$采样噪声添加到输入$\mathbf{x}$，从而产生扰动点${\mathbf{x}}^{\prime }=\mathbf{x}+ϵ$，预期是$E[{\mathbf{x}}^{\prime }]=\mathbf{x}$。

在标准暂退法正则化中，通过按保留（未丢弃）的节点的分数进行规范化来消除每一层的偏差。
换言之，每个中间活性值$h$以暂退概率$p$由随机变量$h^{\prime }$替换，如下所示：

$$\begin{array}{r}{h}^{\prime }=\{\begin{array}{ll}0& \text{ 概率为 }p\\ \frac{h}{1-p}& \text{ 其他情况}\end{array}\end{array}$$

根据此模型的设计，其期望值保持不变，即$E[h^{\prime }]=h$。（$E[h^{\prime }]=p\ast 0+1-p\ast \frac{h}{1-p}$）这样子可以保证期望不变，让训练时候进行dropout，测试时候不进行dropout，同时可不需让训练时候神经网络层数翻倍。

2. 从零开始实现

要实现单层的暂退法函数，我们从均匀分布$U[0,1]$中抽取样本，样本数与这层神经网络的维度一致。然后我们保留那些对应样本大于$p$的节点，把剩下的丢弃。

在下面的代码中，(我们实现 dropout_layer 函数，该函数以dropout的概率丢弃张量输入X中的元素)，如上所述重新缩放剩余部分：将剩余部分除以1.0-dropout。

（1）dropout操作

import torch
from torch import nn
from d2l import torch as d2l


def dropout_layer(X, dropout):
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃
    if dropout == 1:
        return torch.zeros_like(X)
    # 在本情况中，所有元素都被保留
    if dropout == 0:
        return X
    mask = (torch.rand(X.shape) > dropout).float()
    return mask * X / (1.0 - dropout)

（1）torch.rand(X.shape) > dropout：大于dropout时候返回True，小于时候返回False。
（2）(torch.rand(X.shape) > dropout).float()：再使用float()，将True和False分别变成0和1
（3）X * mask：代表选中或者不选中某一神经元

###（2）测试dropout操作

X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1.))

tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0.,  0.,  4.,  0.,  0., 10., 12.,  0.],
        [16., 18., 20., 22.,  0., 26.,  0.,  0.]])
tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.]])

（3）定义模型参数

同样，我们使用Fashion-MNIST数据集。 我们定义具有两个隐藏层的多层感知机，每个隐藏层包含256个单元。

num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256

（4）定义模型

我们可以将暂退法应用于每个隐藏层的输出（在激活函数之后）， 并且可以为每一层分别设置暂退概率： 常见的技巧是在靠近输入层的地方设置较低的暂退概率。 下面的模型将第一个和第二个隐藏层的暂退概率分别设置为0.2和0.5， 并且暂退法只在训练期间有效。

dropout1, dropout2 = 0.2, 0.5

class Net(nn.Module):
    def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
                 is_training = True):
        super(Net, self).__init__()
        self.num_inputs = num_inputs
        self.training = is_training
        self.lin1 = nn.Linear(num_inputs, num_hiddens1)
        self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
        self.lin3 = nn.Linear(num_hiddens2, num_outputs)
        self.relu = nn.ReLU()

    def forward(self, X):
        H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
        # 只有在训练模型时才使用dropout
        if self.training == True:
            # 在第一个全连接层之后添加一个dropout层
            H1 = dropout_layer(H1, dropout1)
        H2 = self.relu(self.lin2(H1))
        if self.training == True:
            # 在第二个全连接层之后添加一个dropout层
            H2 = dropout_layer(H2, dropout2)
        out = self.lin3(H2)
        return out


net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

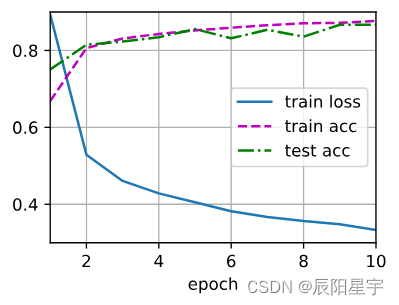
（5）训练和测试

num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

3. 简洁实现

net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),
        nn.ReLU(),
        # 在第一个全连接层之后添加一个dropout层
        nn.Dropout(dropout1),
        nn.Linear(256, 128),
        nn.ReLU(),
        # 在第二个全连接层之后添加一个dropout层
        nn.Dropout(dropout2),
        nn.Linear(128, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

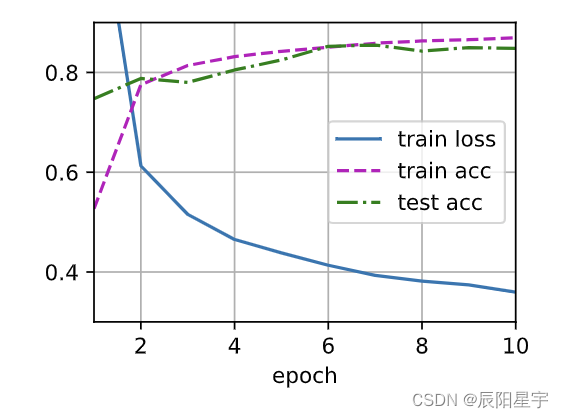
测试和训练

trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

参考文章：暂退法（Dropout）