目录
标准卷积
卷积的运算
conv2d
conv1d
其他卷积类型
空洞卷积(膨胀卷积)
反卷积(转置卷积)
深度可分离卷积
分组卷积
参考文章
上学时,卷积常在各个课程中出现,现代、信号与系统这些,加上前面学习深度学习中有使用过卷积,但具体是什么情况还是没有明白,我觉得问题有二,其一是简单考试可能卷积都考不到,没有仔细思考过具体前后的实现过程。其二是本人天资比较愚钝,理解能力没有到位。
这里结合着pytorch,力求能把自己搞懂!
标准卷积
目前标准卷积是主流的卷积方式。
输出尺寸的计算公式:
参数的含义:
- n:特征图的宽或者高
- k:卷积核的尺寸
- p:padding的数值,一般指单侧填充几个单元
- stride:步长
卷积的运算
卷积的本质就是用卷积核的参数提取原始数据的特征,通过矩阵点乘的运算,提取出和卷积核特征一致的值,如果卷积层有多个卷积核,则神经网络会自动学习卷积核的参数值,使得每个卷积核代表着一个特征。
这里使用的pytorch中最常用的就是conv2d和conv1d,来说明卷积过程计算。
conv2d
conv2d是二维度卷积,对数据在宽和高两个维度进行卷积。
import torch.nn as nn
nn.functional.conv2d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1)
input
:输入的特征图Tensor,形状为(batch_size, in_channels, height, width)。其中,batch_size是批次大小,in_channels是输入特征图的通道数,height和 width是输入特征图的高度和宽度。weight
:卷积核的权重,形状为(out_channels, in_channels/groups, kernel_height, kernel_width)。其中,out_channels是输出特征图的通道数,kernel_height和 kernel_width是卷积核的高度和宽度。
bias:可选的偏置张量。如果指定了偏置,每个输出通道都将添加偏置,一般不管这个。stride
:卷积核的步幅,可以是一个整数或一个长度为2的元组 (stride_height, stride_width)。默认值为 1,表示使用步幅为 1 进行卷积。padding
:是否对输入数据填充0。Padding可以将输入数据的区域改造成卷积核大小的整数倍,这样对不满足卷积核大小的部分数据就不会忽略了,通过padding参数指定填充区域的高度和宽度,默认为0(就是填充区域为0,不填充的意思)。dilation
:卷积核的膨胀率,卷积核之间的空格,默认为1。groups
:输入和输出通道之间的连接方式,通常不用这个参数可以不管。
测试代码:
import torch
from torch.autograd import Variable
import torch.nn.functional as F
print("conv2d sample:")
a=torch.ones(4,4)
x = Variable(a)
x=x.view(1,1,4,4)
print("x variable:", x)
b=torch.ones(2,2)
b[0,0]=0.1
b[0,1]=0.2
b[1,0]=0.3
b[1,1]=0.4
weights = Variable(b)
weights=weights.view(1,1,2,2)
print ("weights:",weights)
y=F.conv2d(x, weights, padding=0)
print ("y:",y)控制台:
conv2d sample:
x variable: tensor([[[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]]])
weights: tensor([[[[0.1000, 0.2000],
[0.3000, 0.4000]]]])
y: tensor([[[[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]]]])这里我来看看它是怎样的一个运算过程:

原始数据大小是,这里的
我们不管它,就是一个样本,而每个样本一个通道的意思。
说明每个通道的数据是
大小的。而卷积核的大小为
。最后卷积的结果为
。
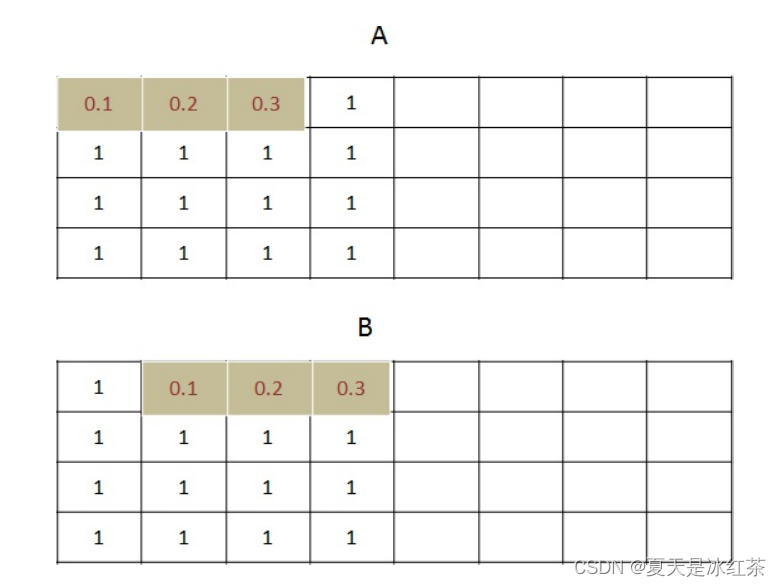
首先,卷积核与原始数据第一个数据做卷积乘法。如图中示例A:0.1*1+0.2*1+0.3*1+0.4*1=1.0。
其次,按照顺序移动卷积核,并且和目标区域做矩阵乘法。得到这一步的卷积值,作为结果矩阵的一个元素。如图中示例B:0.1*1+0.2*1+0.3*1+0.4*1=1.0。
最后,用卷积核卷积input[2:4,2:4],最后共四个元素。如图中示例C,算法相同最后的值也是1。
由于原始数据都为1,所以卷积后得到的结果相同。如上控制台中的信息‘y’。
conv1d
conv1d是一维卷积,它和conv2d的区别在于只对宽度进行卷积,对高度不卷积。
import torch.nn as nn
nn.functional.conv1d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1)
- input:输入的Tensor数据,格式为 (batch,channels,W),三维数组,第一维度是样本数量,第二维度是通道数或者记录数,三维度是宽度。
- weight:卷积核权重,也就是卷积核本身。是一个三维数组,(out_channels, in_channels/groups, kW)。out_channels 是卷积核输出层的神经元个数,也就是这层有多少个卷积核;in_channels 是输入通道数;kW 是卷积核的宽度。
- bias:位移参数,可选项,一般也不用管。
- stride:滑动窗口,默认为 1,指每次卷积对原数据滑动 1 个单元格。
- padding:是否对输入数据填充 0。Padding 可以将输入数据的区域改造成是卷积核大小的整数倍,这样对不满足卷积核大小的部分数据就不会忽略了。通过 padding 参数指定填充区域的高度和宽度,默认 0(就是填充区域为0,不填充的意思)。
- dilation:卷积核之间的空格,默认 1。
- groups:将输入数据分组,通常不用管这个参数,没有太大意义。
测试代码:
import torch
from torch.autograd import Variable
import torch.nn.functional as F
print("conv1d sample:")
a=range(16)
x = Variable(torch.Tensor(a))
x=x.view(1,1,16)
print("x variable:", x)
b=torch.ones(3)
b[0]=0.1
b[1]=0.2
b[2]=0.3
weights = Variable(b)
weights=weights.view(1,1,3)
print ("weights:",weights)
y=F.conv1d(x, weights, padding=0)
print ("y:",y)控制台:
conv1d sample:
x variable: tensor([[[ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11., 12., 13.,
14., 15.]]])
weights: tensor([[[0.1000, 0.2000, 0.3000]]])
y: tensor([[[0.8000, 1.4000, 2.0000, 2.6000, 3.2000, 3.8000, 4.4000, 5.0000,
5.6000, 6.2000, 6.8000, 7.4000, 8.0000, 8.6000]]])这里我来看看它是怎样的一个运算过程:
最开始,原始数据大小是 0-15 的一共 16 个数字,卷积核宽度是 3,向量是 [0.1,0.2,0.3]。
我们看第一个卷积是对 x[0:3] 共 3 个值 [0,1,2] 进行卷积,公式如下:0*0.1+1*0.2+2*0.3=0.8
对第二个目标卷积,是 x[1:4] 共 3 个值 [1,2,3] 进行卷积,公式如下:1*0.1+2*0.2+3*0.3=1.4
其余过程,略......
计算结果与控制台中打印出的内容相同。
上图就是conv1d的示意图,和conv2d的区别就是只对宽度卷积,不对高度卷积。最后结果的宽度是原始数据的宽度减去卷积核的宽度再加上1,这里就是 14。
我们在来看看输入数据有多个通道的情况:
测试代码:
import torch
from torch.autograd import Variable
import torch.nn.functional as F
print("conv1d sample:")
a=range(16)
x = Variable(torch.Tensor(a))
x=x.view(1,2,8)
print("x variable:", x)
b=torch.ones(6)
b[0]=0.1
b[1]=0.2
b[2]=0.3
weights = Variable(b)
weights=weights.view(1,2,3)
print ("weights:",weights)
y=F.conv1d(x, weights, padding=0)
print ("y:",y)控制台:
conv1d sample:
x variable: tensor([[[ 0., 1., 2., 3., 4., 5., 6., 7.],
[ 8., 9., 10., 11., 12., 13., 14., 15.]]])
weights: tensor([[[0.1000, 0.2000, 0.3000],
[1.0000, 1.0000, 1.0000]]])
y: tensor([[[27.8000, 31.4000, 35.0000, 38.6000, 42.2000, 45.8000]]])这里我们就来看看返回的第一个元素27.8是怎么计算的,这时候卷积核有两个通道。
[0.1,0.2,0.3]和[1,1,1]
(1)第1个卷积对象也有2个通道:[0,1,2]和[8,9,10]
结果是2个卷积核分别对应2个输入通道进行卷积然后求和。
卷积核是对第1个卷积对象的卷积值:(0.1*0+0.2*1+0.3*2)+(1*8+1*9+1*10)=27.8
(2)第2个卷积对象也有2个通道:[1,2,3] 和 [9,10,11]
卷积核对第 2 个卷积对象的卷积值:(0.1*1+0.2*2+0.3*3)+(1*9+1*10+1*11)=31.4
计算出来的结果也与控制台得到的相同。
其他卷积类型
卷积除了标准卷积还有空洞卷积、反卷积、深度可分离卷积、分组卷积等等。
空洞卷积(膨胀卷积)
在卷积核大小相同的情况下,空洞卷积的滑窗元素之间存在着一些间隙,这些间隙在空洞卷积中叫膨胀因子(dilated_ratio)。
普通的卷积就是dilated_ratio=1的时候。(如下图示例)
(dilated_ratio - 1) 的值则为塞入的空格数,这里dilated_ratio我们简写为d,假定原卷积核大小为 k,那么塞入了 (d - 1) 个空格后的卷积核大小 size 为:
空洞卷积输出特征图大小计算公式为:
参数的含义:
- n:特征图的宽或者高
- k:卷积核的尺寸
- p:padding的数值,一般指单侧填充几个单元
- stride:步长
- d:d-1的值为塞入的空格数
普通的卷积:

kernel_size=3, stride=1, padding=0
空洞卷积:

kernel_size = 3, dilated_ratio = 2, stride = 1, padding = 0
我们这里使用pytorch来实现一下
import torch
import torch.nn as nn
class DilatedConv(nn.Module):
# 定义一个包含空洞卷积的模型
def __init__(self):
super(DilatedConv, self).__init__()
self.dilated_conv = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, dilation=2)
# dilation=2,空洞率(膨胀率),指定了卷积核中的空洞大小。在这里,设置为2表示每隔一个像素进行卷积计算,相当于在水平和垂直方向上引入了一个间隔。
self.relu = nn.ReLU()
def forward(self, x):
out = self.dilated_conv(x)
out = self.relu(out)
return out
model = DilatedConv()
input_data = torch.randn(1, 3, 32, 32) # 假设输入尺寸为 32x32,通道数为 3
output = model(input_data)
print(output.size())最后输出的结果是torch.Size([1, 64, 28, 28]),我们来仔细推究一下如何从输入(1, 3, 32, 32)转为这个结果的。
首先,输入数据的尺寸为(1, 3, 32, 32),其中1是批次大小,3是输入通道数,32x32是输入图像的高度和宽度。
然而,空洞卷积的参数设置为in_channels=3、out_channels=64、kernel_size=3和dilation=2。由于填充默认为0,卷积操作的输出特征图尺寸计算公式为:
输出高度 = (输入高度 + 2 * padding - dilation * (kernel_size - 1) - 1) / stride + 1
输出宽度 = (输入宽度 + 2 * padding - dilation * (kernel_size - 1) - 1) / stride + 1
在这里,stride默认为1,padding默认为0。
根据上述公式,计算输出特征图的尺寸:
输出高度 = (32 + 2 * 0 - 2 * (3 - 1) - 1) / 1 + 1 = 28
输出宽度 = (32 + 2 * 0 - 2 * (3 - 1) - 1) / 1 + 1 = 28
因此,输出特征图的尺寸为(1, 64, 28, 28),其中1是批次大小,64是输出通道数,28x28是输出特征图的高度和宽度。
反卷积(转置卷积)
卷积是对输入图像提取出特征(可能尺寸会变小),“反卷积”便是进行相反的操作。但这里说是“反卷积”并不严谨,因为并不会完全还原到跟输入图像一样,一般是还原后的尺寸与输入图像一致,主要用于向上采样。从数学计算上看,“反卷积”相当于是将卷积核转换为稀疏矩阵后进行转置计算,因此,也被称为“转置卷积”。

在2x2的输入图像上应用步长为1、边界全0填充的3x3卷积核,进行转置卷积(反卷积)计算,向上采样后输出的图像大小为4x4。
我们这里使用pytorch来实现一下
import torch
import torch.nn as nn
class TransposedConv(nn.Module):
# 定义转置卷积模型
def __init__(self):
super(TransposedConv, self).__init__()
self.transposed_conv = nn.ConvTranspose2d(in_channels=3, out_channels=64, kernel_size=3, stride=2, padding=1)
self.relu = nn.ReLU()
def forward(self, x):
out = self.transposed_conv(x)
out = self.relu(out)
return out
model = TransposedConv()
input_data = torch.randn(1, 3, 16, 16) # 假设输入尺寸为 16x16,通道数为 3
output = model(input_data)
print(output.size())输入数据的尺寸为 (1, 3, 16, 16),其中 1 是批次大小,3 是输入通道数,16x16 是输入图像的高度和宽度。
转置卷积层的计算公式如下:
输出高度 = (输入高度 - 1) * stride - 2 * padding + dilation * (kernel_size - 1) + output_padding + 1
输出宽度 = (输入宽度 - 1) * stride - 2 * padding + dilation * (kernel_size - 1) + output_padding + 1
在这里,stride 默认为 2,padding 默认为 1,dilation 默认为 1,output_padding 默认为 0。
根据上述公式,计算输出特征图的尺寸:
输出高度 = (16 - 1) * 2 - 2 * 1 + 1 * (3 - 1) + 0 + 1 = 31
输出宽度 = (16 - 1) * 2 - 2 * 1 + 1 * (3 - 1) + 0 + 1 = 31
因此,输出特征图的尺寸应为 (1, 64, 31, 31),其中 1 是批次大小,64 是输出通道数,31x31 是输出特征图的高度和宽度。
深度可分离卷积
深度可分离卷积主要由两步组成:深度卷积和1x1卷积。
完整的过程如下:
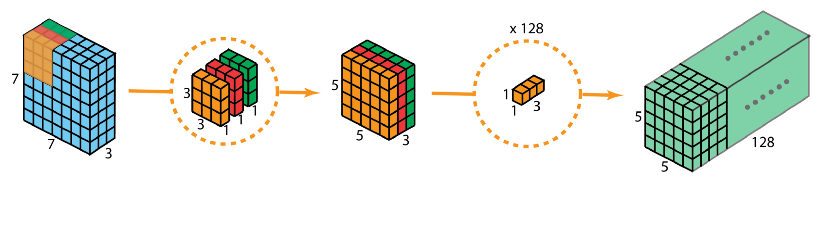
实现流程
首先,在输入层上应用深度卷积。使用3个卷积核分别对输入层的3个通道作卷积计算,再堆叠在一起。再使用1x1的卷积(3个通道)进行计算,得到只有1个通道的结果。 重复多次1x1的卷积操作(如上x128),最后便会得到一个深度的卷积结果。
我们这里使用pytorch来实现一下
import torch
import torch.nn as nn
class DepthwiseSeparableConv(nn.Module):
# 定义深度可分离卷积模型
def __init__(self, in_channels, out_channels):
super(DepthwiseSeparableConv, self).__init__()
self.depthwise_conv = nn.Sequential(
nn.Conv2d(in_channels, in_channels, kernel_size=3, groups=in_channels, padding=1),
nn.ReLU(),
nn.BatchNorm2d(in_channels)
)
self.pointwise_conv = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=1),
nn.ReLU(),
nn.BatchNorm2d(out_channels)
)
def forward(self, x):
out = self.depthwise_conv(x)
out = self.pointwise_conv(out)
return out
model = DepthwiseSeparableConv(in_channels=3, out_channels=64)
input_data = torch.randn(1, 3, 32, 32) # 假设输入尺寸为 32x32,通道数为 3
output = model(input_data)
print(output.size())输出是torch.Size([1, 64, 32, 32]),这里倒是没问题。
- 深度卷积部分:self.depthwise_conv 包含一个 nn.Conv2d 层,输入通道数为 3,输出通道数也为 3,卷积核大小为 3x3,填充为 1。深度卷积操作将在输入上应用一个 3x3 的卷积核,并在每个通道上进行独立的卷积计算。这会生成一个大小为 (1, 3, 32, 32) 的特征图。
- 逐点卷积部分:self.pointwise_conv 包含一个 nn.Conv2d 层,输入通道数为 3,输出通道数为 64,卷积核大小为 1x1。逐点卷积操作将在每个位置上对所有输入通道的像素进行加权求和,生成一个输出通道数为 64 的特征图。这会生成一个大小为 (1, 64, 32, 32) 的特征图。
因此,根据上述描述,输入 (1, 3, 32, 32) 经过深度可分离卷积模型的操作后,得到输出 (1, 64, 32, 32)。
要注意的是,这里的深度可分离卷积模型中的深度卷积和逐点卷积操作是连续应用的,没有使用池化层或其他降采样操作,因此输出尺寸与输入尺寸相同。
分组卷积
2012年,AlexNet论文中最先提出来的概念,当时主要为了解决GPU显存不足问题,将卷积分组后放到两个GPU并行执行。
在分组卷积中,卷积核被分成不同的组,每组负责对相应的输入层进行卷积计算,最后再进行合并。如下图,卷积核被分成前后两个组,前半部分的卷积组负责处理前半部分的输入层,后半部分的卷积组负责处理后半部分的输入层,最后将结果合并组合。
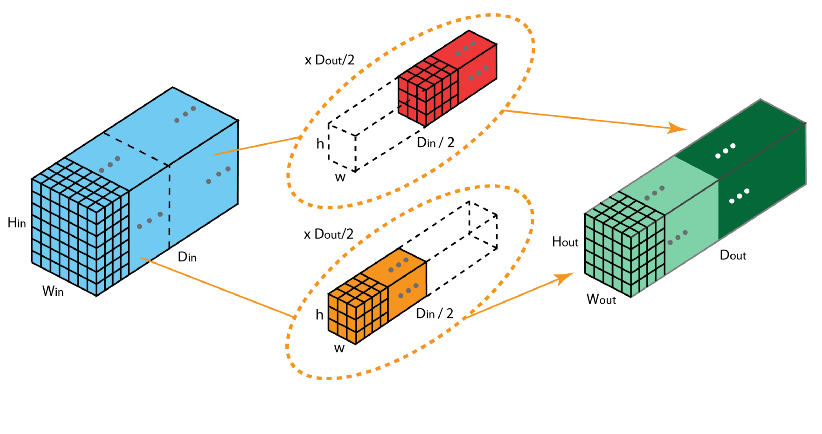
我们这里使用pytorch来实现一下
import torch
import torch.nn as nn
class GroupConvModel(nn.Module):
# 定义一个包含分组卷积的模型
def __init__(self):
super(GroupConvModel, self).__init__()
self.group_conv = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=3, groups=3)
self.relu = nn.ReLU()
def forward(self, x):
out = self.group_conv(x)
out = self.relu(out)
return out
model = GroupConvModel()
input_data = torch.randn(1, 6, 32, 32) # 假设输入尺寸为 32x32,通道数为 6
output = model(input_data)
print(output.size())输出为torch.Size([1, 12, 30, 30]),输入是(1, 6 ,32 ,32 )
- 分组卷积部分:self.group_conv 包含一个 nn.Conv2d 层,输入通道数为 6,输出通道数为 12,卷积核大小为 3x3,分组数为 3。分组卷积操作将输入的 6 个通道分成 3 组,每组 2 个通道,然后在每组内进行独立的卷积计算。这会生成一个大小为 (1, 12, 30, 30) 的特征图。
- ReLU激活:将分组卷积后的特征图通过 ReLU 激活函数进行非线性处理。
因此,根据上述描述,输入 (1, 6, 32, 32) 经过分组卷积模型的操作后,得到输出 (1, 12, 30, 30)。
分组卷积的输出尺寸会因为分组数和卷积核大小而有所变化。在这个例子中,输入的 6 个通道被分成了 3 组,每组 2 个通道,然后对每组内的通道应用了 3x3 的卷积核。这导致输出特征图的高度和宽度分别减小了 2 个像素。
参考文章
(1条消息) 空洞卷积(膨胀卷积)的相关知识以及使用建议(HDC原则)_膨胀卷积和空洞卷积_Le0v1n的博客-CSDN博客
图解AI:各种类型的卷积-标准卷积、反卷积、可分离卷积、分组卷积等_涵小呆的博客-CSDN博客