题目来源:https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/
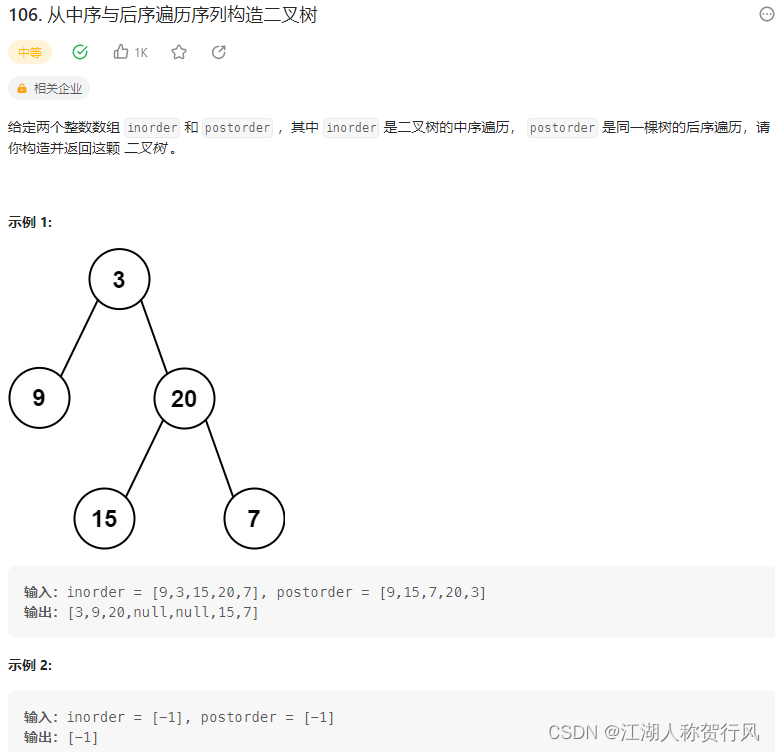

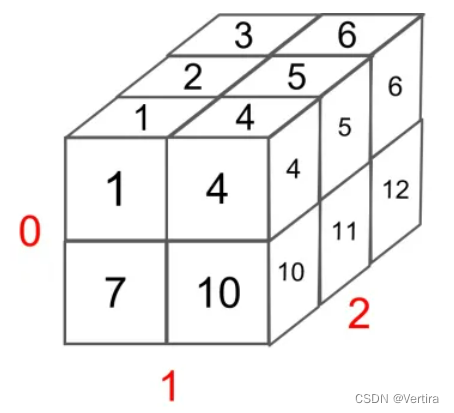
C++题解:中序遍历是左中右,后序遍历是左右中,所以拿到两个遍历数组,我们可以从后序遍历获取中间节点,再通过中间节点在中序遍历的索引,可以将中序遍历的左右子树分割开,根据左子树的长度也可以将后序遍历的左右子树分割开。
进行遍历时,我们需要分别找到左右子树,所以每次遍历,都需要单独获取左子树的中序和后序遍历数组、右子树的中序和后序遍历数组。当无左右子树时,返回空指针;当左右子树为叶子节点时,返回当前节点。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int len = postorder.size();
if(len == 0) return nullptr;
TreeNode* root = new TreeNode(postorder[len-1]);
if(len == 1) return root;
// 寻找中间节点postorder[len-1]在中序数组的索引
int ind = find(inorder.begin(), inorder.end(), postorder[len-1]) - inorder.begin();
// 中间节点的左子树的中序遍历和后续遍历
vector<int> inleft(inorder.begin(), inorder.begin() + ind);
vector<int> postleft(postorder.begin(), postorder.begin() + ind);
root->left = buildTree(inleft, postleft);
// 中间节点的右子树的中序遍历和后续遍历
vector<int> inright(inorder.begin() + ind + 1, inorder.end());
vector<int> postright(postorder.begin() + ind, postorder.end() - 1);
root->right = buildTree(inright, postright);
return root;
}
};