b站刘二大人《PyTorch深度学习实践》课程第三讲梯度下降笔记与代码:https://www.bilibili.com/video/BV1Y7411d7Ys?p=3&vd_source=b17f113d28933824d753a0915d5e3a90
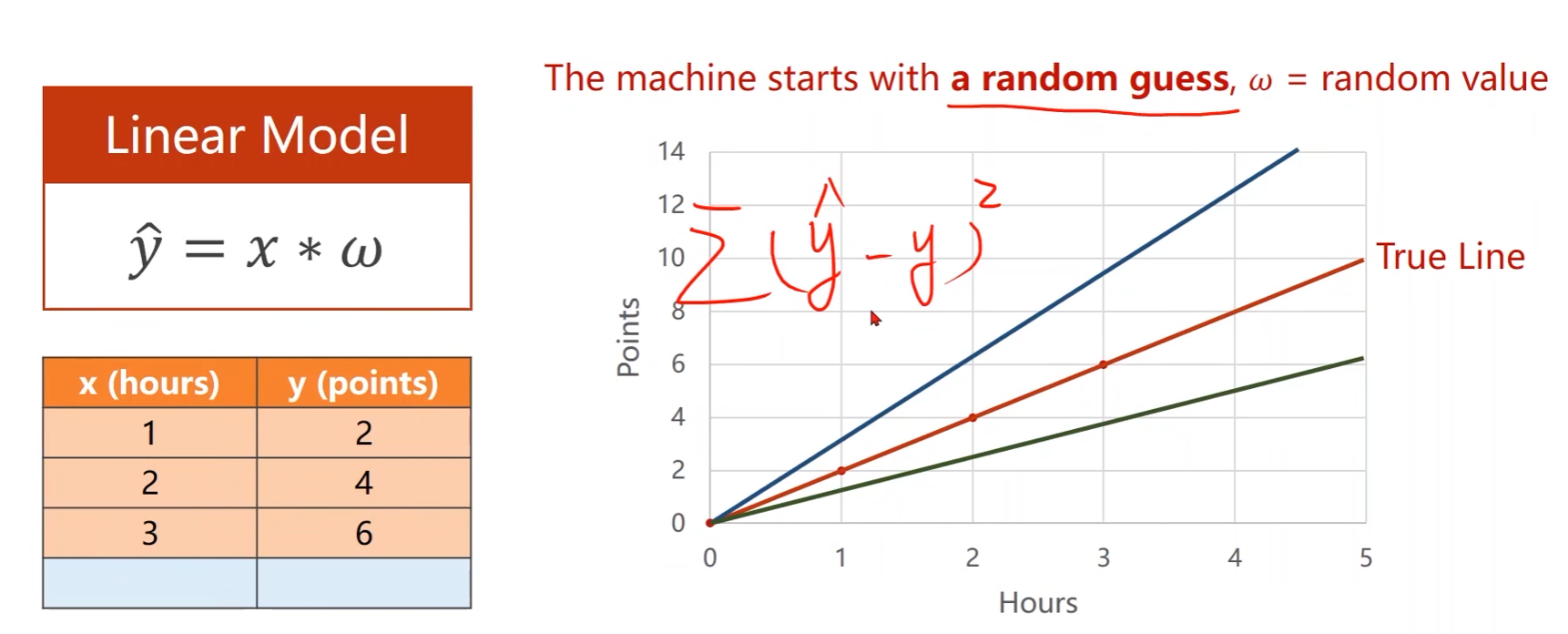
上一讲例子中,初始权重 w w w是随机给的,然后计算每个样本 x x x的预测值 y ^ \hat{y} y^与真实值 y y y的误差平方,再算整个训练集的均方根误差,选择最小的均方根误差对应的权重值
-
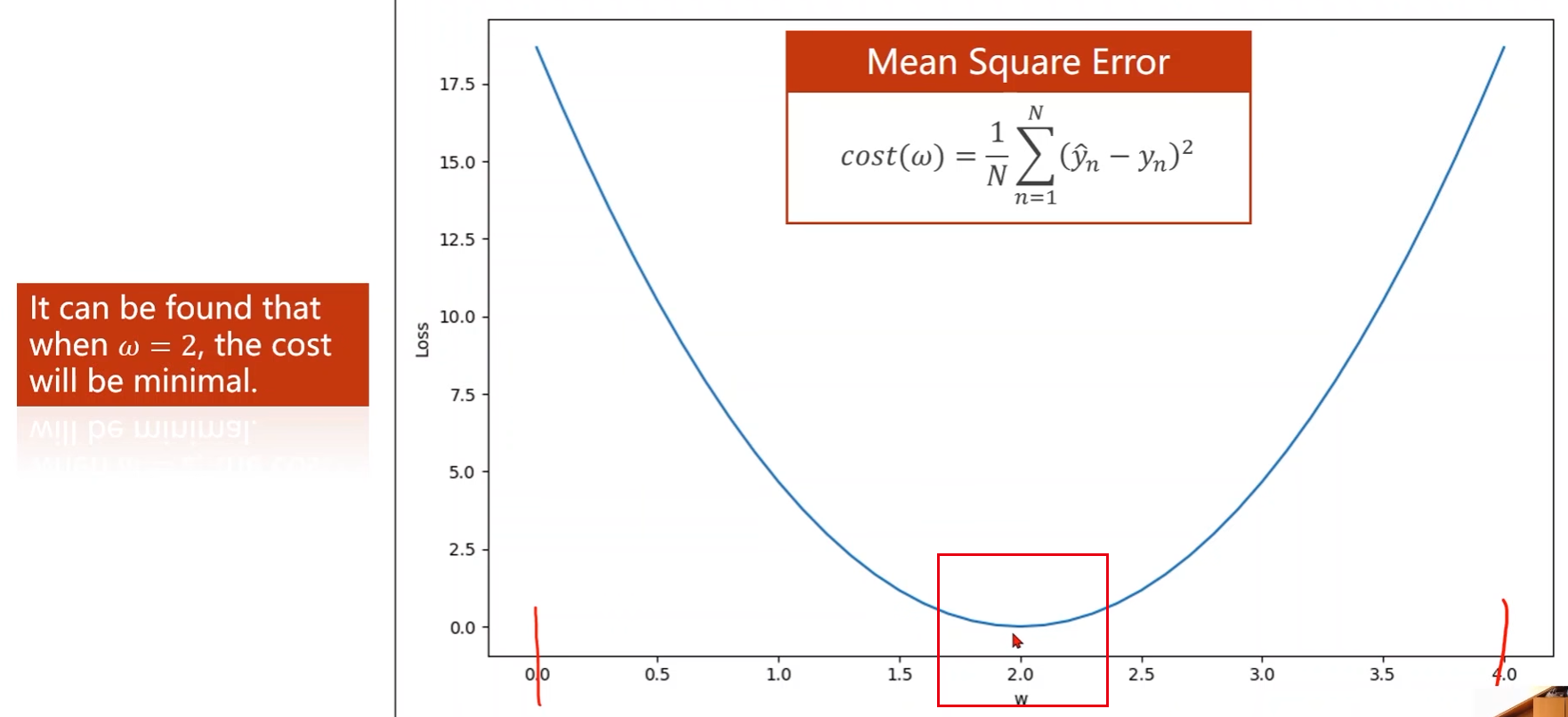
上一讲中采用的是穷举法来确定权重值,即先确定权重值的一个大概范围,然后再里面进行采样,计算每个权重值 w w w的误差,最后选择误差最小的那个权重值
存在的问题:
- 在实际的学习任务中,损失函数
c
o
s
t
(
w
)
cost(w)
cost(w)并不是图中这种理想曲线
- 一维的时候还可以使用线性搜索,但如果有两个权重 y ^ ( w 1 , w 2 , x ) \hat{y}(w_1,w_2,x) y^(w1,w2,x),那么就是在一个平面中进行搜索,一维如果是搜索100次,那么在二维的时候就是100的平方,权重再多点那么搜索量将会更大
分治法:
-
先进行稀疏的搜索,认为结果在值较小的区域,然后再在值较小的区域内进行稀疏的搜索,以此往复……
-
问题:容易陷入局部最优;高维度无法搜索
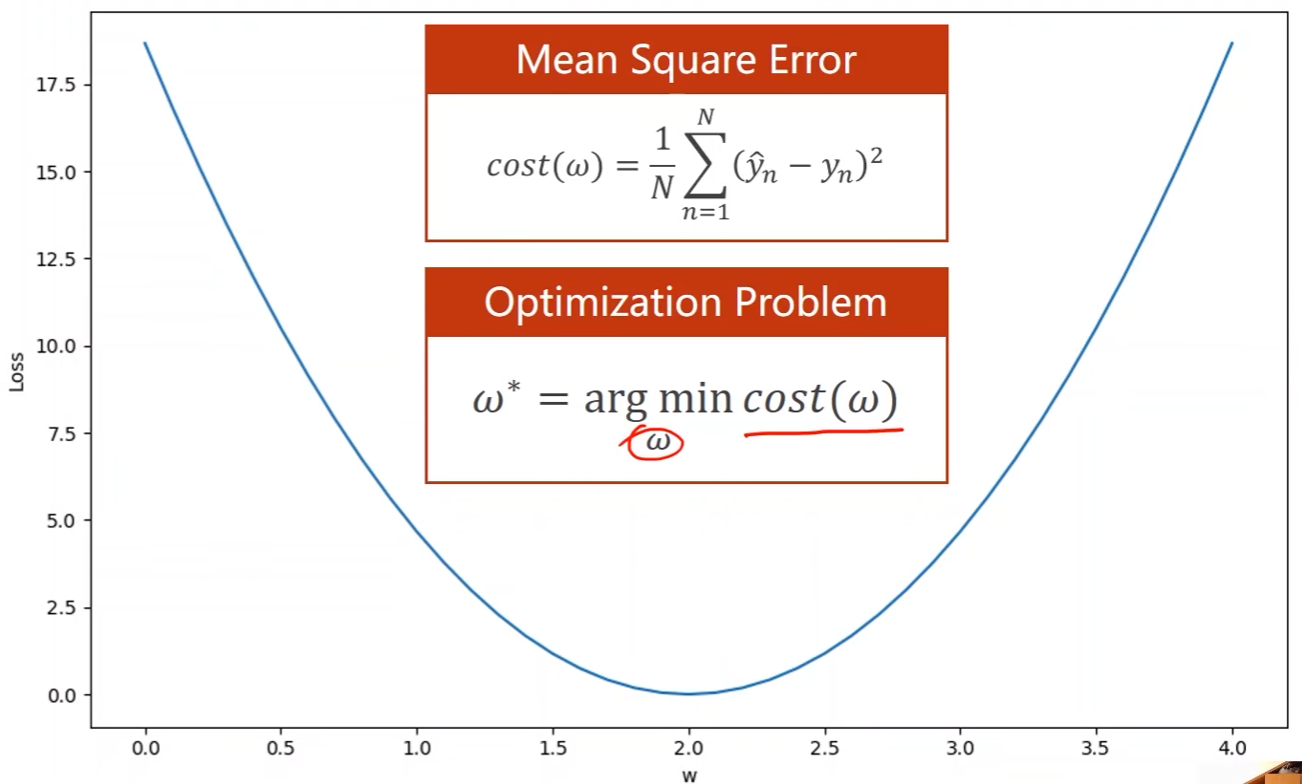
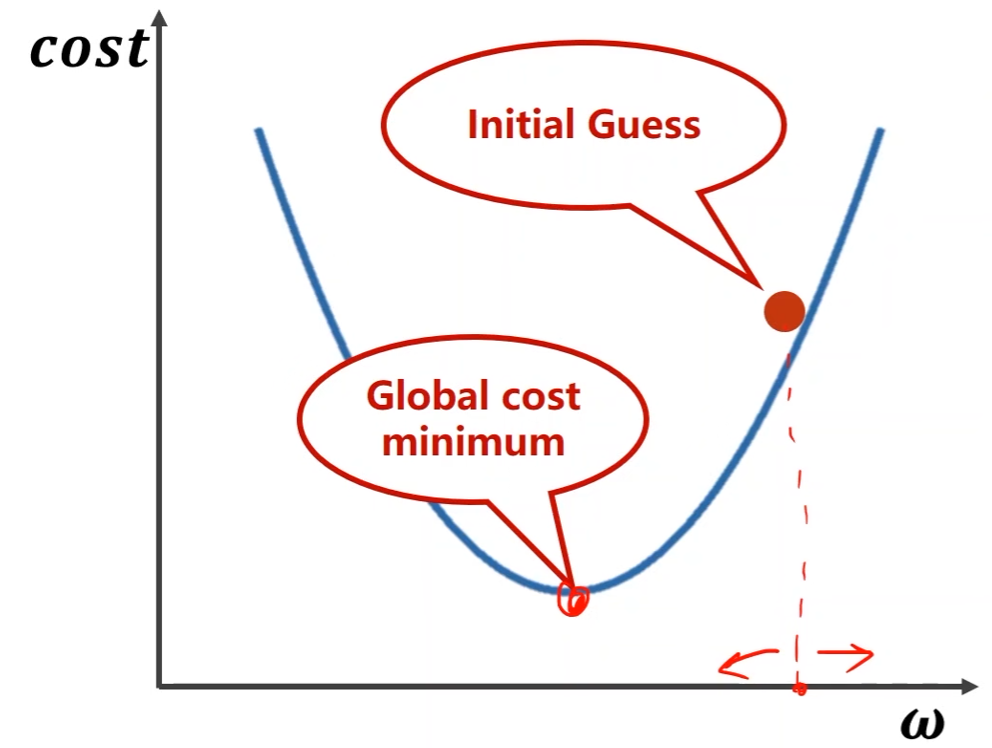
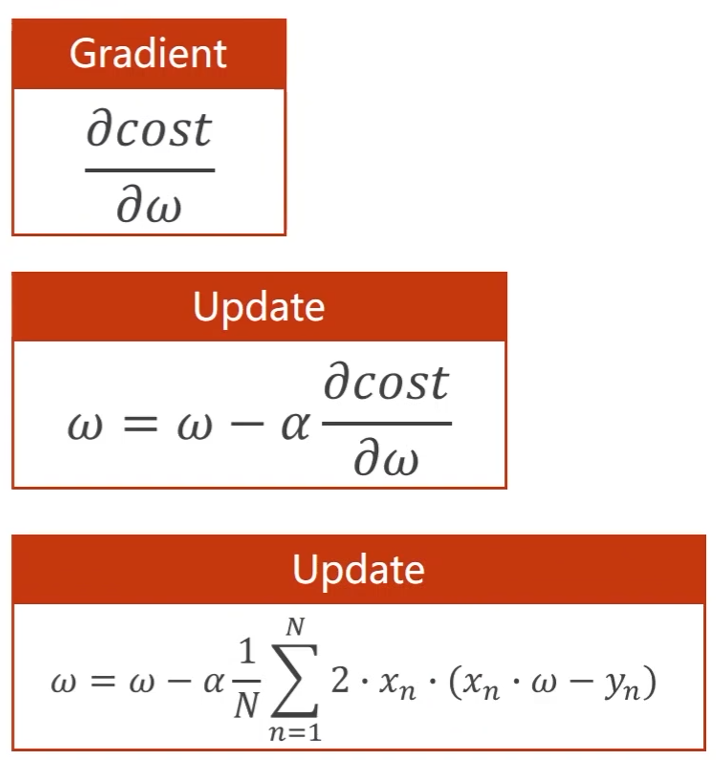
将使目标函数最小的问题定义为优化问题:
Gradient Descent,梯度下降法:
-
有一个初始猜测值,但需要确定搜索方向?
-
采用梯度确定搜索方向
-
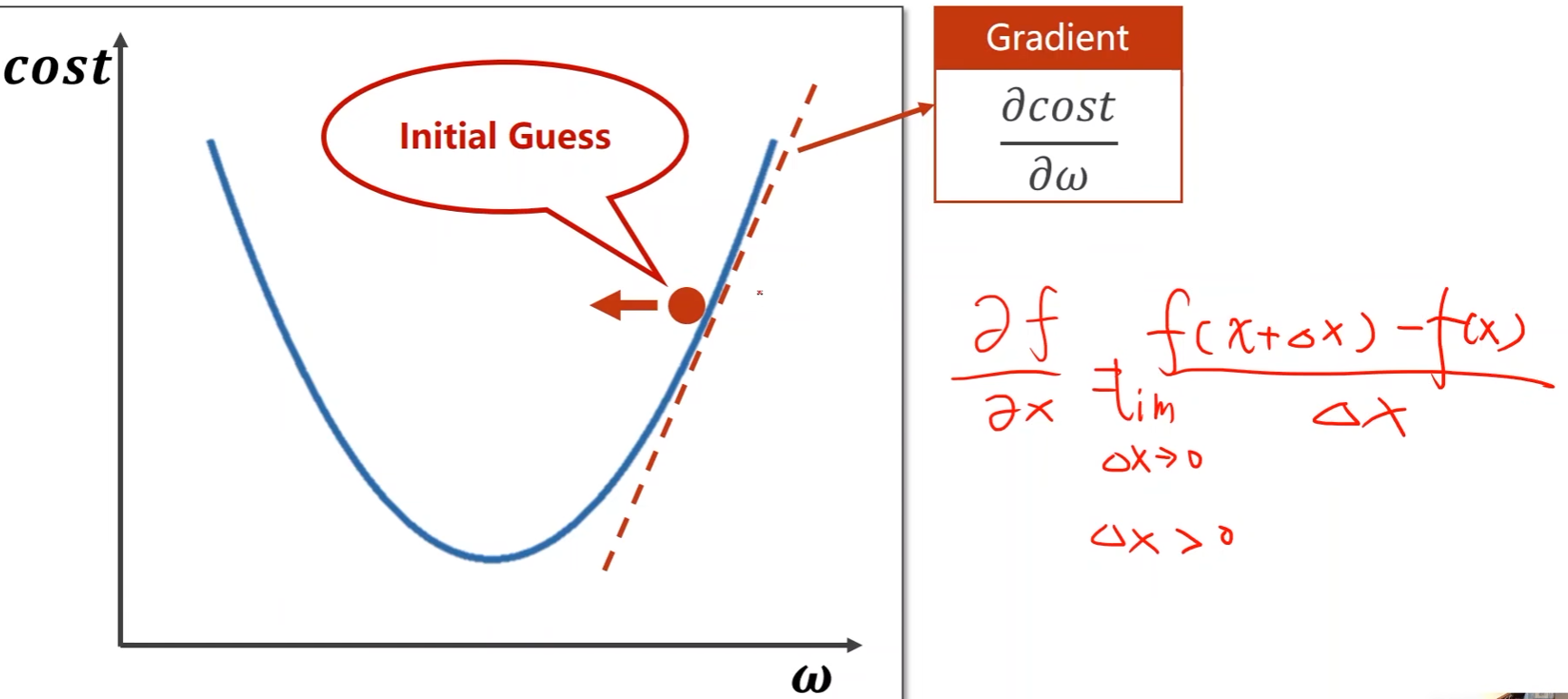
对代价函数 c o s t cost cost求关于权重 w w w的导数,可以得到上升方向
-
Δ x \Delta x Δx大于0,如果导数大于0,意味着 x x x加上 Δ x \Delta x Δx后函数变大了,即往正方向是上升的;如果导数小于0,意味着随着 x x x的增加函数在减小,即往负方向是上升的
-
-
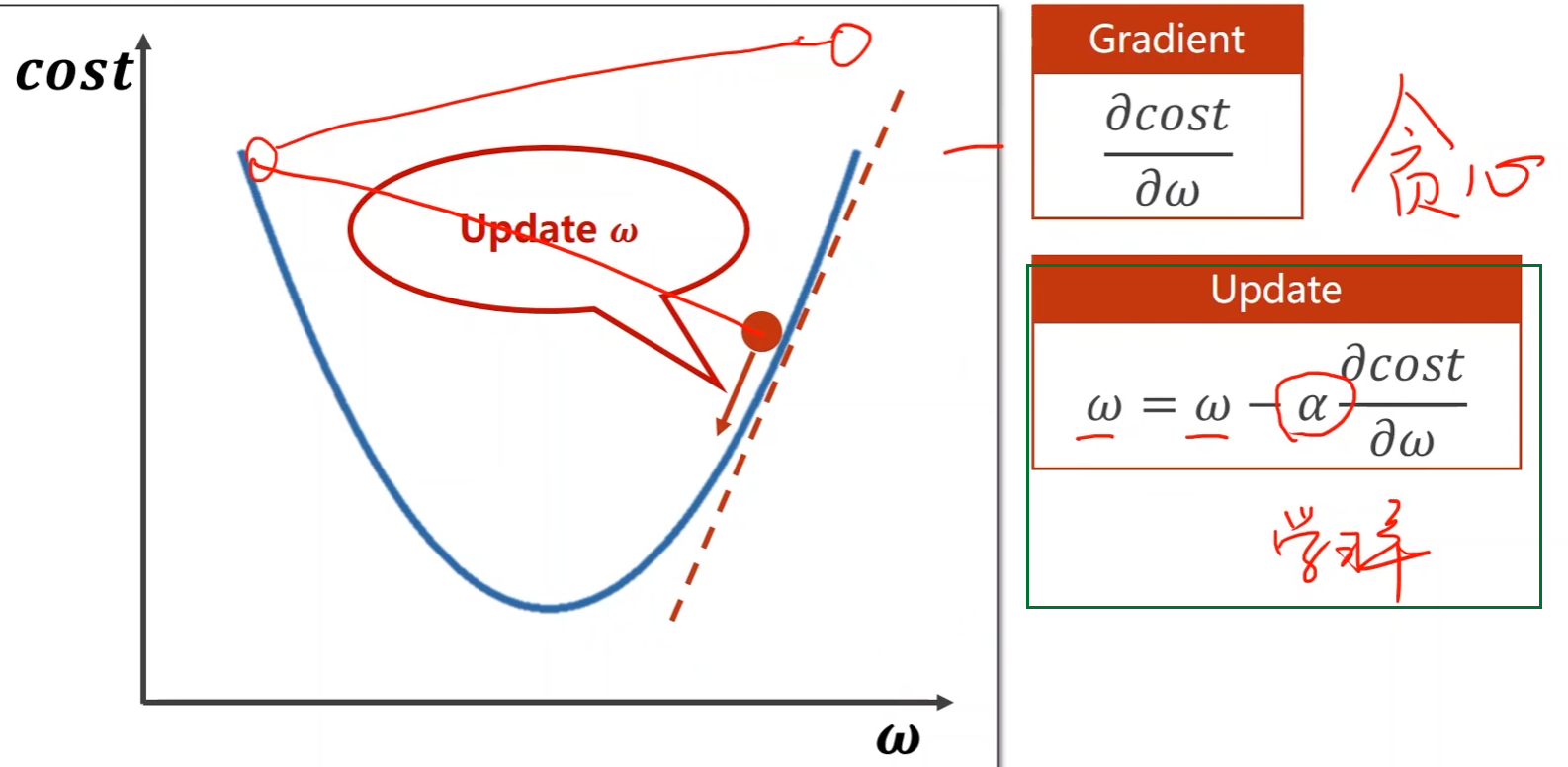
往梯度的负方向搜索(下降最快的方向),可以得到最小值
- α \alpha α是学习率,即搜索步长
-
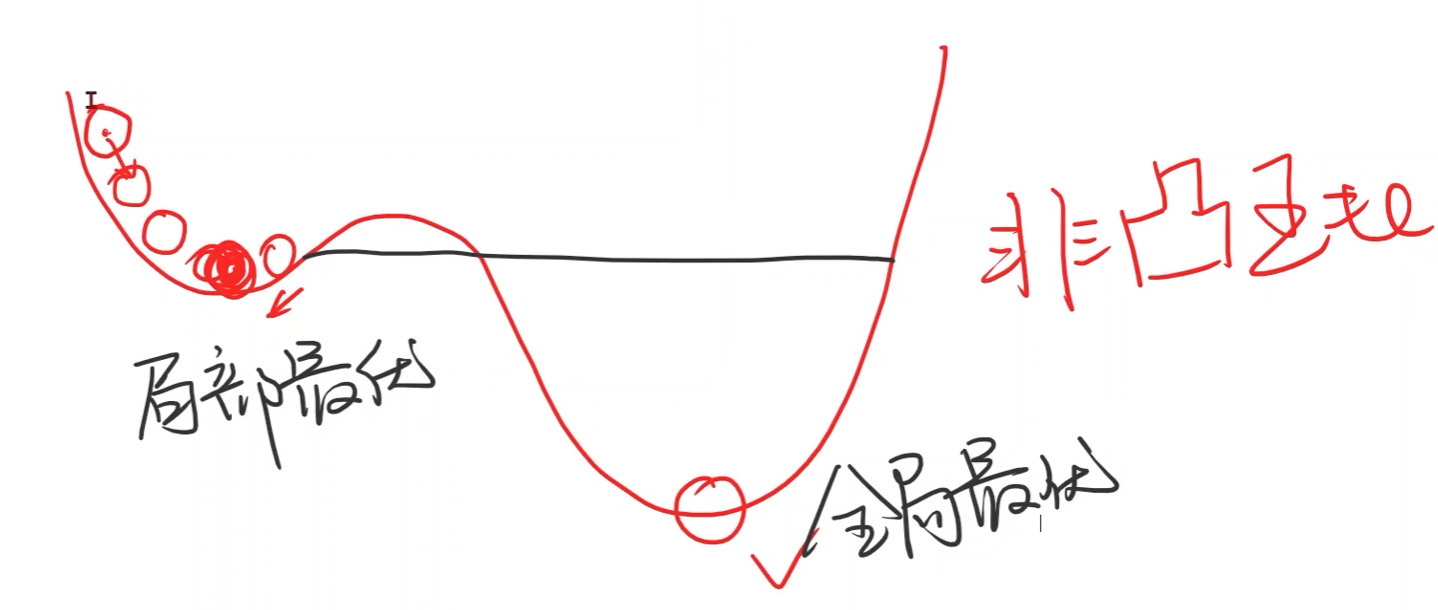
梯度下降法只能保证找到局部最优点,不一定能找到全局最优
- 实际深度学习问题中的损失函数并没有很多的局部最优点,不容易陷入局部最优点
-
鞍点:梯度等于0(马鞍面)
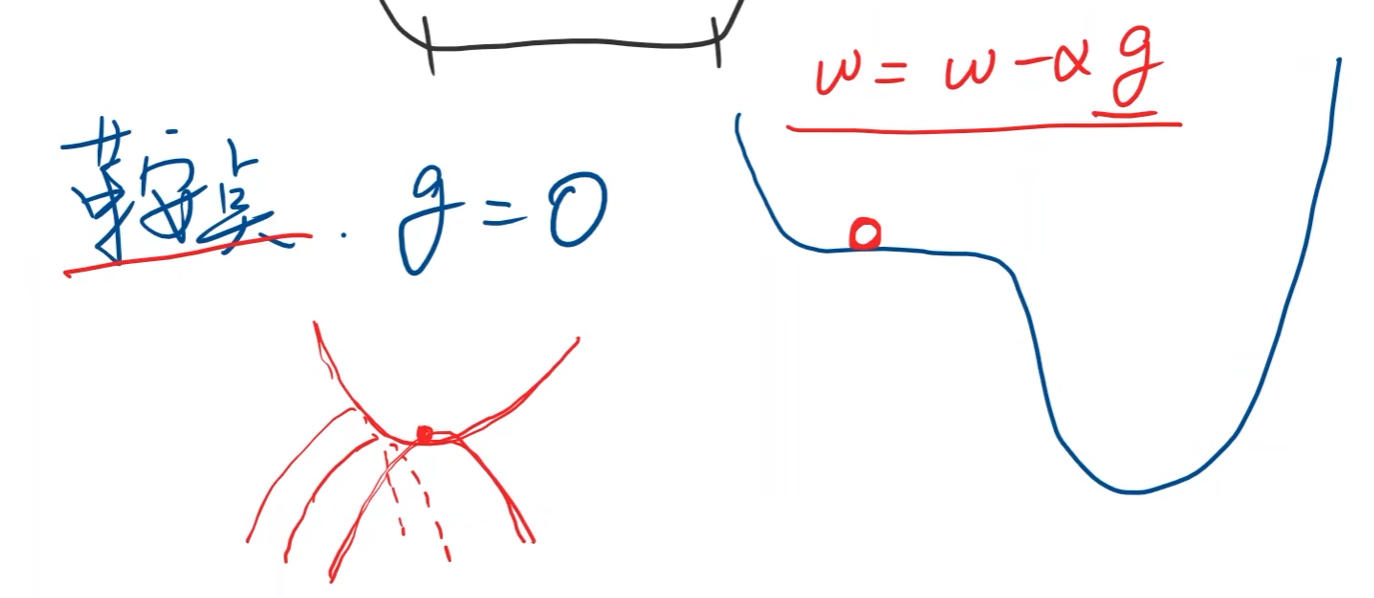
-
接下去就是反复求梯度,往梯度负方向搜索
梯度计算看原视频20:17处,老师讲的很详细

代码实现:
import numpy as np
import matplotlib.pyplot as plt
# 训练集
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 初始权重的猜测值
w = 1.0
# 存储训练轮数以及对应的loss值用于绘图
epoch_list = []
cost_list = []
def forward(x):
# 定义模型:y_hat = x * w
return x * w
def cost(xs, ys):
# 定义代价函数cost(w)。xs就是x_data, ys就是y_data
cost = 0
for x, y in zip(xs, ys):
y_pred = forward(x) # y_hat
cost += (y_pred - y) ** 2 # (y_hat - y)^2,然后再累加
return cost / len(xs) # 累加后再除样本数量N,即MSE公式中的1/N
def gradient(xs, ys):
# 计算梯度,即对cost(w)求关于w的偏导
grad = 0
for x, y in zip(xs, ys):
grad += 2 * x * (x * w - y) # 累加部分
return grad / len(xs) # 除样本数量N
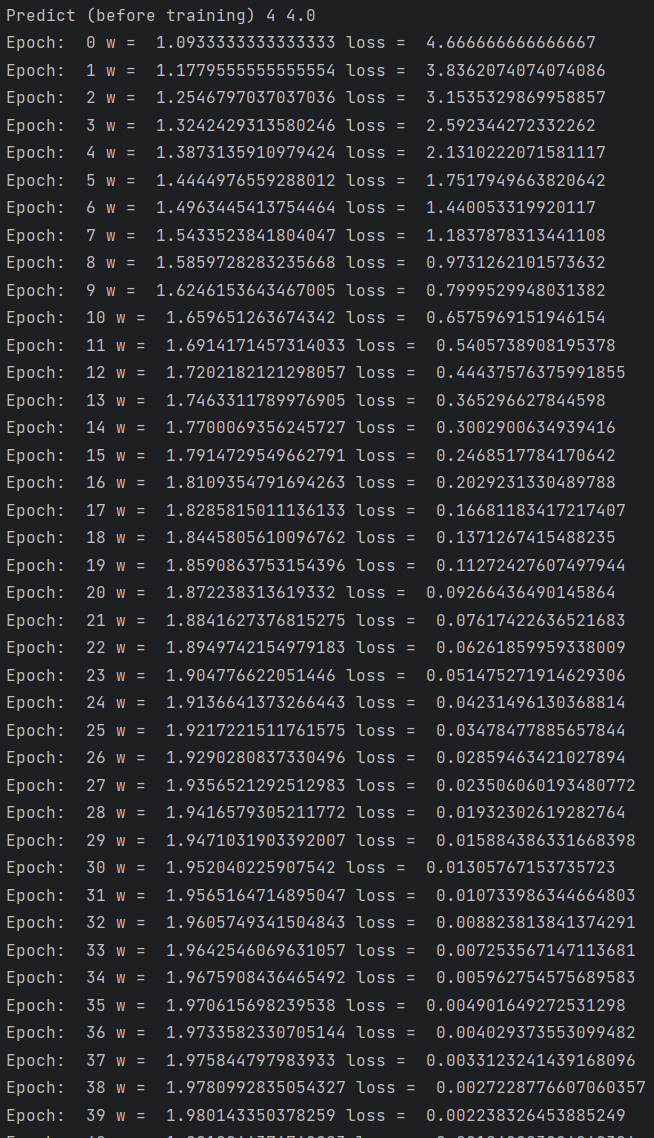
print('Predict (before training)', 4, forward(4))
# 训练过程,迭代100次(100轮训练)
# 每次都是将权重w减去学习率乘以梯度
for epoch in range(100):
cost_val = cost(x_data, y_data) # 当前步的损失值
grad_val = gradient(x_data, y_data) # 当前的梯度
w -= 0.01 * grad_val # 更新权重w,0.01是学习率
print('Epoch: ', epoch, 'w = ', w, 'loss = ', cost_val) # 打印每一轮训练的日志
epoch_list.append(epoch)
cost_list.append(cost_val)
print('Predict (after training)', 4, forward(4))
# loss曲线绘制,x轴是epoch,y轴是loss值
plt.plot(epoch_list, cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()
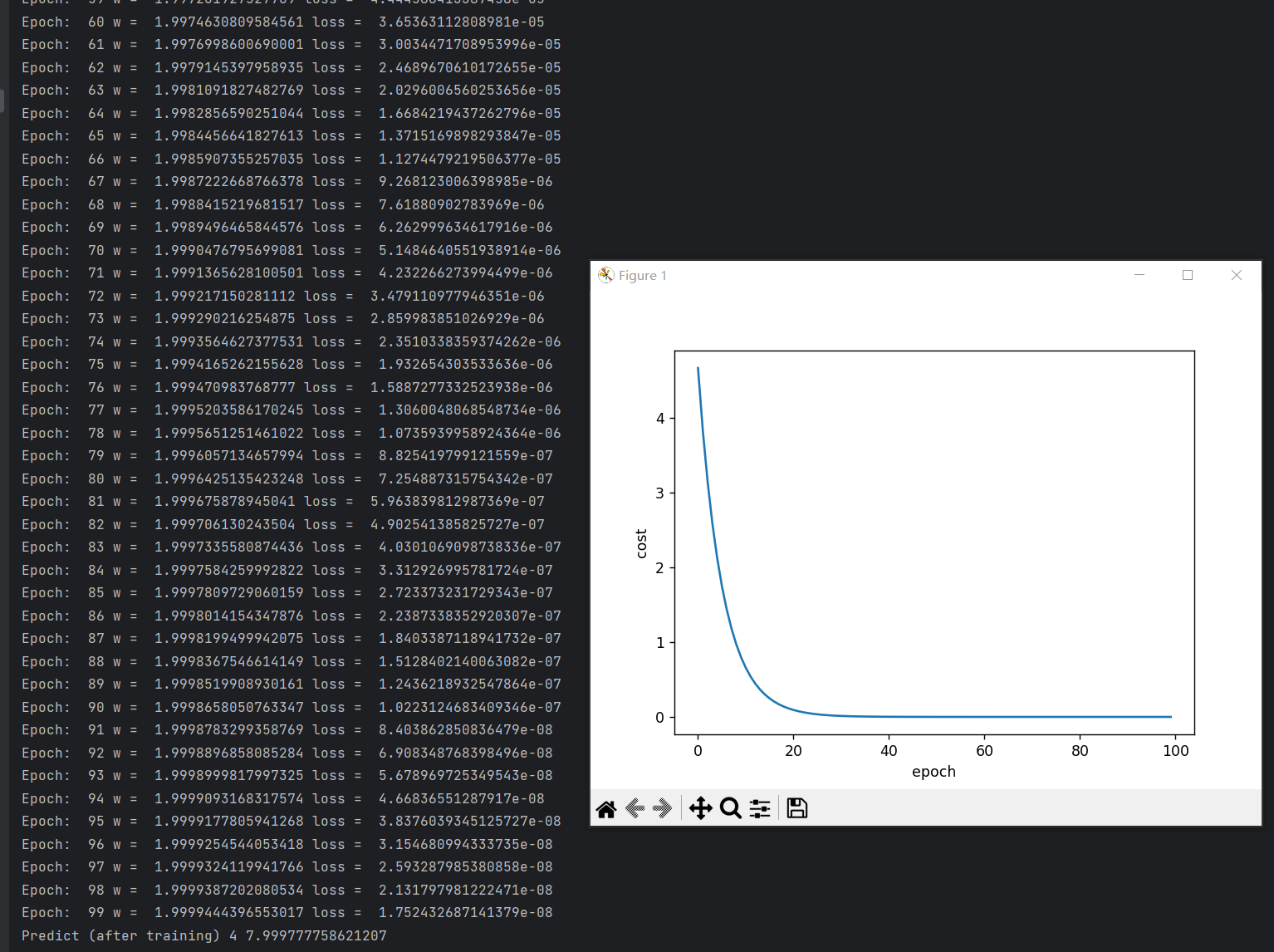
实际中的训练曲线一般存在波动,但总体上是收敛的
- 绘图的时候一般会采用指数加权均值来对曲线做平滑处理,以便观察训练趋势

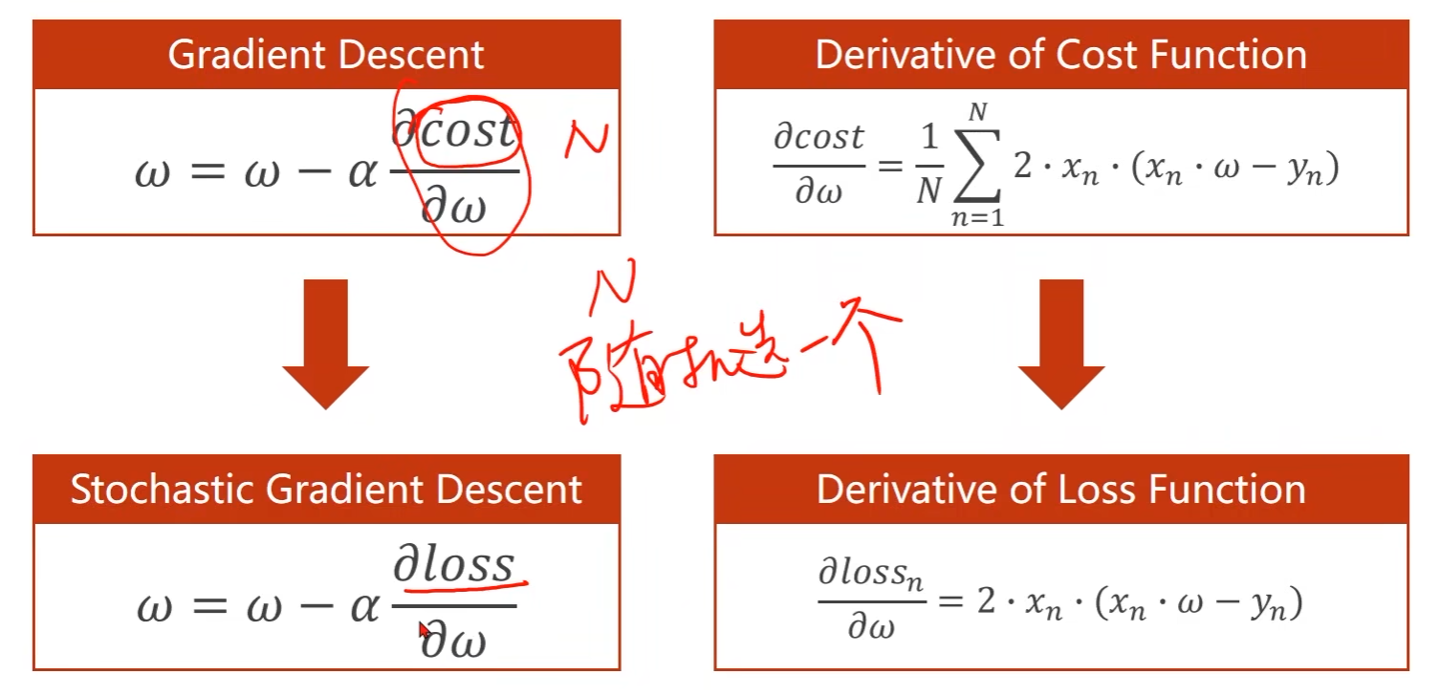
梯度下降法在实际中应用较少,用的比较多的是它的衍生版本,随机梯度下降
Stochastic Gradient Descent
- 梯度下降法中是对数据集的损失cost进行梯度更新
- 提供N个数据,随机梯度下降是从这N个数据中随机选一个,将其损失loss来更新,即单个样本的损失对权重求导
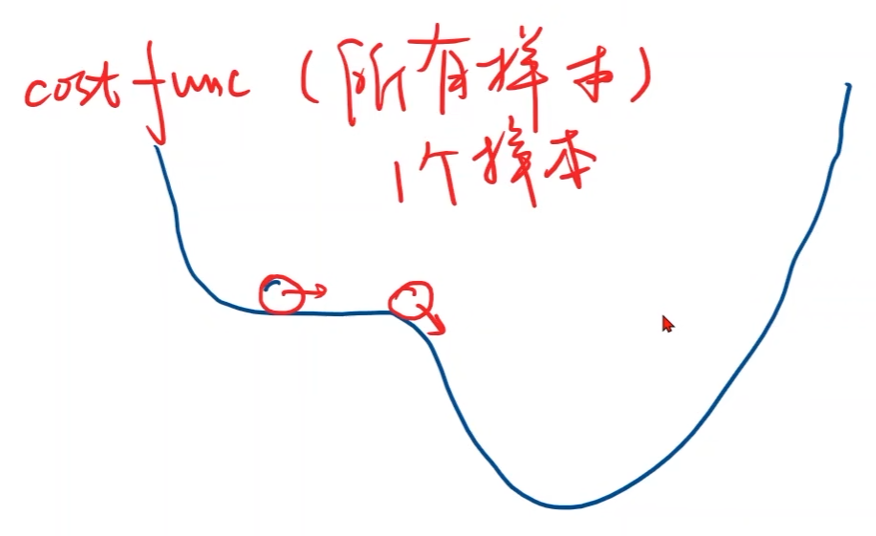
使用随机梯度下降的原因:
-
cost function曲线存在鞍点
-
每次随机取1个样本,会引入了随机噪声,那么即便陷入鞍点,随机噪声可能会对其进行推动,那么有可能离开鞍点
代码实现:
import matplotlib.pyplot as plt
# 训练集
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 初始权重的猜测值
w = 1.0
# 存储训练轮数以及对应的los值用于绘图
epoch_list = []
cost_list = []
def forward(x):
# 定义模型:y_hat = x * w
return x * w
def loss(x, y):
# 计算loss function
y_pred = forward(x) # y_hat
return (y_pred - y) ** 2 # (y_hat - y)^2
def gradient(x, y):
# 计算梯度
return 2 * x * (x * w - y)
print('Predict (before training)', 4, forward(4))
# 训练过程
for epoch in range(100):
for x, y in zip(x_data, y_data):
grad = gradient(x, y) # 对每一个样本求梯度
w = w - 0.01 * grad # 用一个样本的梯度来更新权重,而不是所有的
print("\tgrad: ", x, y, grad)
l = loss(x, y)
print("progress: ", epoch, "w = ", w, "loss = ", l)
print('Predict (after training)', 4, forward(4))
在实际问题中,梯度下降中对 f ( x i ) f(x_i) f(xi)求导和对 f ( x i + 1 ) f(x_{i+1}) f(xi+1)求导是没有关联的,相互独立,因此是可以进行并行计算的
但是在随机梯度下降中,对 w w w求导,但是 w w w是要更新的,因此下一步的权重更新与上一步的更新结果之间存在关系,即不可进行并行计算
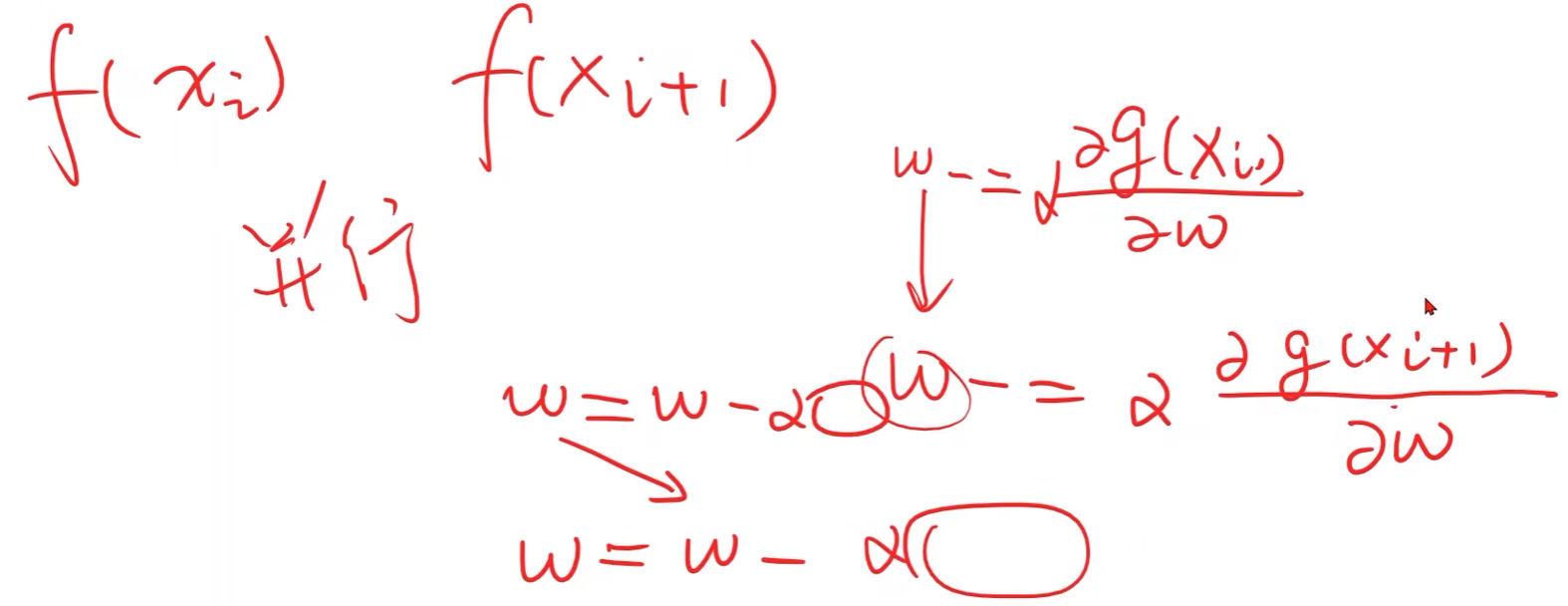
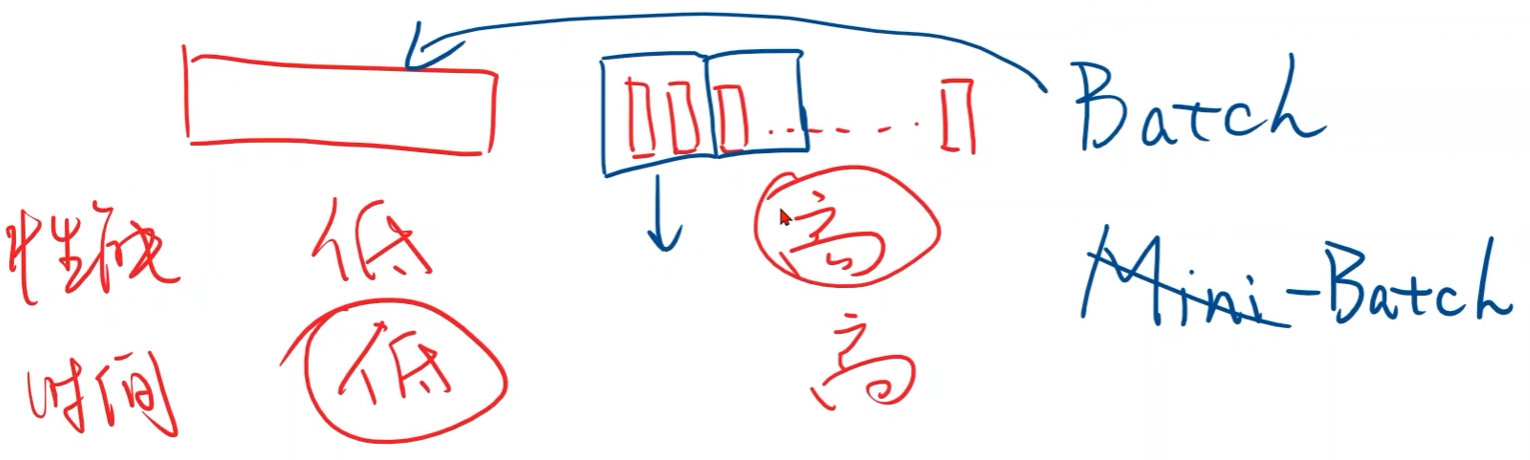
- 梯度下降法可以并行计算,时间复杂度低,但学习器的性能差
- 随机梯度下降无法并行计算,时间复杂度高,但学习器的性能好
采用折中的方法:Batch,批量
批量随机梯度下降:
- 若干个样本一组,每次用这一组样本的梯度进行权重更新