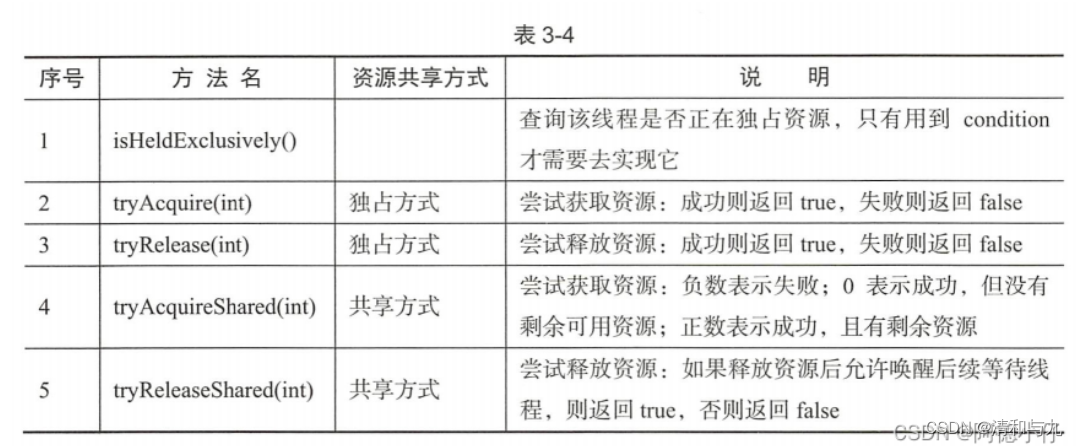
文章目录
- (一)负采样
- (二)GloVe
- 1.带全局语料库的跳元模型
- 2.GloVe模型
- 3.问题
- 4.跳元模型与GloVe模型的比较
- (三)问题
- 1.参数初始化
- 2.梯度下降
- 3.下游任务
- 4.句法信息
- 5.似然估计
- 6.词向量表示
(一)负采样
首先我们回顾一下之前所学word2vec模型的条件概率公式:
P
(
w
o
∣
w
c
)
=
e
x
p
(
u
o
T
v
c
)
∑
i
∈
V
e
x
p
(
u
i
T
v
c
)
P(w_o|w_c)=\frac{exp(u_o^Tv_c)}{\sum_{i\in V}exp(u_i^Tv_c)}
P(wo∣wc)=∑i∈Vexp(uiTvc)exp(uoTvc)
注意到每次计算条件概率,我们都需要遍历一次语料库,以求将条件概率值压至
(
0
,
1
)
(0,1)
(0,1)范围内。
这样做的开销是巨大的;同时,因为我们只更新窗口中出现过的词向量表示,所以反向传播计算的巨大的梯度矩阵具有严重的稀疏性问题(大量资源被浪费掉)。
我们尝试对这一概率公式进行优化。
当前模型优化的目的是使中心词向量
v
v
v和上下文词向量
u
u
u共现概率尽可能的大,我们发现下面的公式也可以很好的表示这一目的:
P
(
D
=
1
∣
w
c
,
w
o
)
=
σ
(
u
o
T
v
c
)
σ
(
x
)
=
1
1
+
e
x
p
(
−
x
)
P(D=1|w_c,w_o)=\sigma(u_o^Tv_c)\\ \sigma(x)=\frac1{1+exp(-x)}
P(D=1∣wc,wo)=σ(uoTvc)σ(x)=1+exp(−x)1
但很快我们就会发现一个问题:调整公式之后模型优化的方向,是试图使每一个词向量变为无穷大,这显然没有任何意义。
为了使目标函数更有意义,负采样添加了为条件概率公式添加了负样本
w
k
w_k
wk:
P
(
w
o
∣
w
c
)
=
P
(
D
=
1
∣
w
c
,
w
o
)
∏
k
P
(
D
=
0
∣
w
c
,
w
k
)
P(w_o|w_c)=P(D=1|w_c,w_o)\prod^k{P(D=0|w_c,w_k)}
P(wo∣wc)=P(D=1∣wc,wo)∏kP(D=0∣wc,wk)
对于上述公式,上下文词
w
o
w_o
wo是与中心词
w
c
w_c
wc共现的正样本,噪声词
w
k
w_k
wk是与中心词
w
c
w_c
wc不共现的负样本。模型优化的方向是使正样本共现概率尽可能的大,负样本的共现概率尽可能的小。
现在,我们进行反向传播时不需要再去计算整个语料库的梯度矩阵,只需要计算正负样本的梯度然后更新即可,很好地解决了稀疏性问题。
以下是负采样实现代码:
def get_negatives(all_contexts, vocab, counter, k):
"""
返回负采样中的噪声词
:param k 噪声词数量
:param all_contexts 二维列表,所有中心词对应的上下文(必须数字化,否则无法比较噪声词和上下文词)
:param counter 词频统计数据
:param vocab 词典
:return all_negatives 二维列表,所有中心词对应的噪声词
"""
sampling_weights = [counter[vocab.idx2token[i]] ** 0.75 # 采样频率=词频 ** (3/4)
for i in range(1, len(vocab))] # 索引为0的是被排除的未知标记
all_negatives, generator = [], RandomGenerator(sampling_weights)
for contexts in all_contexts:
negatives = [] # 每个上下文词对应的k个噪声词
while len(negatives) < len(contexts) * k:
neg = generator.draw()
if neg not in contexts: # 噪声词不能是上下文词
negatives.append(neg)
all_negatives.append(negatives)
return all_negatives
The,a等高频词并不会给我们带来很多信息,但人们没有发现到底词频(概率)多小才算好。
所以我们在进行负采样时,将原词频分布以函数 f ( x ) = x 3 4 f(x)=x^{\frac34} f(x)=x43处理得到采样词频,以期减少高频词的采样。
(二)GloVe
1.带全局语料库的跳元模型
我们用共现矩阵累计窗口中出现的词的次数:
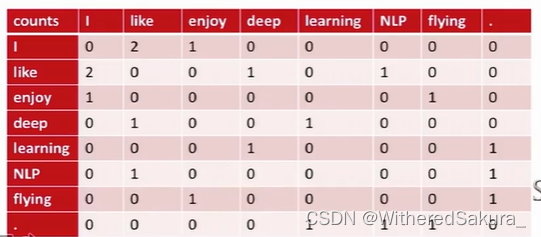
使用这样的全局语料库统计,跳元模型的损失函数变为:
−
∑
i
∈
V
∑
j
∈
V
x
i
j
l
o
g
q
i
j
-\sum_{i\in V}\sum_{j\in V}{x_{ij}}\ log\ q_{ij}
−i∈V∑j∈V∑xij log qij
其中
q
i
j
q_{ij}
qij表示
w
i
w_i
wi与
w
j
w_j
wj的共现概率;而
x
i
j
x_{ij}
xij表示
w
i
w_i
wi作为中心词时,
w
j
w_j
wj与其共现的次数。
有了全局语料库的辅助,上述损失函数优化出的词向量表示的条件分布会更加接近全局语料库统计中的条件分布。
2.GloVe模型
GloVe建立损失函数的思想与跳元模型有些不同。
基础此前的了解,我们知道优化的目标是使出现在同一上下文窗口中的两个词元 w i w_i wi和 w j w_j wj共现的概率 p i j p_{ij} pij尽可能的大。
那么对于任意三个词元 w i , w j , w k w_i,w_j,w_k wi,wj,wk,其中中心词 w i w_i wi,上下文词 w j , w k w_j,w_k wj,wk:
(1)当两个上下文词均与中心词相关时(如water,ice,steam),有 p i j p i k \frac{p_{ij}}{p_{ik}} pikpij接近于1;
(2)当 w i w_i wi与 w j w_j wj相关,而 w i w_i wi与 w k w_k wk无关时(如water,ice,fashion),有 p i j p i k \frac{p_{ij}}{p_{ik}} pikpij大于1。
对这种关系进行建模,可以有效解决跳元模型中,稀有词向量被赋予过大的权重问题。
利用这种思想,GloVe模型进一步学习词与词之间的关系信息。
f
(
w
i
,
w
j
,
w
k
)
=
p
i
j
p
i
k
f(w_i,w_j,w_k)=\frac {p_{ij}}{p_{ik}}
f(wi,wj,wk)=pikpij
因为这一比值是标量,并且有
f
(
w
i
,
w
j
,
w
k
)
f
(
w
i
,
w
k
,
w
j
)
=
1
f(w_i,w_j,w_k)f(w_i,w_k,w_j)=1
f(wi,wj,wk)f(wi,wk,wj)=1,使用余弦相似度和
e
x
p
(
x
)
exp(x)
exp(x)对其进行建模。
f
(
w
i
,
w
j
,
w
k
)
=
α
e
x
p
(
w
i
T
w
j
)
β
e
x
p
(
w
i
T
w
k
)
f(w_i,w_j,w_k)=\frac{\alpha\ exp(w_i^Tw_j)}{\beta\ exp(w_i^Tw_k)}
f(wi,wj,wk)=β exp(wiTwk)α exp(wiTwj)
其中
α
,
β
\alpha,\beta
α,β是常数。
α
e
x
p
(
w
i
T
w
j
)
=
p
i
j
\alpha\ exp(w_i^Tw_j)=p_{ij}
α exp(wiTwj)=pij
代入
p
i
j
=
x
i
j
x
i
p_{ij}=\frac{x_{ij}}{x_i}
pij=xixij,等式两侧取对数:
l
o
g
α
−
l
o
g
x
i
+
w
i
T
w
j
=
l
o
g
x
i
j
log\ \alpha-log\ x_i+w_i^Tw_j=log\ x_{ij}
log α−log xi+wiTwj=log xij
用两个标量模型参数来拟合
l
o
g
α
−
l
o
g
x
i
log\ \alpha-log\ x_i
log α−log xi:
w
i
T
w
j
+
b
i
+
c
i
=
l
o
g
x
i
j
w_i^Tw_j+b_i+c_i=log\ x_{ij}
wiTwj+bi+ci=log xij
使用加权平方损失:
−
∑
i
∈
V
∑
j
∈
V
h
(
x
i
j
)
(
w
i
T
w
j
+
b
i
+
b
j
)
2
-\sum_{i\in V}\sum_{j\in V}{h(x_{ij})(w_i^Tw_j+b_i+b_j)^2}
−i∈V∑j∈V∑h(xij)(wiTwj+bi+bj)2
其中
h
(
x
i
j
)
h(x_{ij})
h(xij)是权重函数。
以上就是GloVe模型的损失函数。
3.问题
(1)全局语料库统计数据的应用有几个问题:
<1>每当有新的词加入,就需要更新整个共现矩阵;
<2>共现矩阵非常大,但由于窗口大小有限,造成稀疏性问题。
相应的解决办法有两个:
<1>增加信息存储量,不只是存储共同出现的次数,再存储一些其他重要信息;
<2>使用主成分分析、奇异值分解对共现矩阵进行降维(压缩)。
(2)如何进行全局语料库的数据统计?
可以采用常规的计数方式,对窗口中每个出现的词元进行计数。
也可以采用加权计数,例如:对窗口中距离中心词近的上下文词计数为1,较远的计数为0.5(表明关系没有那么密切)。
4.跳元模型与GloVe模型的比较
(1)跳元模型不能有效利用全局语料库统计数据,但在下游任务比较多时,表现更好;
(2)GloVe模型能够有效利用全局语料库统计数据,学习得到的词向量会更加接近全局语料库统计中的条件分布。
(三)问题
1.参数初始化
如何初始化参数,以避免陷入局部最优解?
最简单的初始化方式就是在两个比较小的数值之间随机取值来初始化参数。
2.梯度下降
可以一个窗口一下降,也可以经过多个窗口后再一起下降。
但是不建议遍历所有窗口后再下降,这通常的效果并不怎么好。
3.下游任务
当我们进行word2vec模型的优化的时候,会发生聚类现象:

下游任务的语料库往往不能包含我们的训练语料库,因此如果在下游对词向量表示进行优化,会出现一种严重的问题。
举个例子来说,在上游,telly,TV,television发生了聚类现象,而下游模型优化的只包括TV,television的词向量表示。
因此TV,television发生了移动,而telly不会移动,会导致严重的错误。
所以当下游数据少的时候,不建议训练词向量,而是保持不变;当下游数据多的时候可以进行训练。
4.句法信息
曾经有过相关研究,对语法(比如说,英语语法)进行深度学习而不是对上下文分布,结果并不是很好。
5.似然估计
在估计方面,点积、欧式距离(二维欧式距离就是 x 2 + y 2 x^2+y^2 x2+y2)表现的都很好。
如在英语中,动词与其名词变形总是出现在相似的上下文中,具有相似的欧式距离。
6.词向量表示
每一个词元有两个词向量表示:上下文词向量和中心词向量。
对此,我们在应用词向量表示的时候通常将二者相加,这会表现得更好。
这可能是因为中心词和上下文词关系的对称性(对于窗口 { w 1 , w 2 , . . . , w n } \{w_1,w_2,...,w_n\} {w1,w2,...,wn}来说,取 w 2 w_2 w2为中心词, w 1 w_1 w1是其上下文词,反之亦然),和模型优化的随机性,从而导致将二者相加得到的词向量表示更加稳定。