文章目录

前期知识
股票问题
- 买卖股票的最佳时机 II
- 最佳买卖股票时机含冷冻期
- 买卖股票的最佳时机 IV
- - 补充：恰好k次 / 至少k次怎么做？
相关题目练习
- 买卖股票的最佳时机 https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/
- - 解法1——状态机DP
  - 解法2——贪心
- 买卖股票的最佳时机 III https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/
- 买卖股票的最佳时机含手续费 https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/
- 最大子序列交替和 https://leetcode.cn/problems/maximum-alternating-subsequence-sum/
- - 理解1写法
  - 理解2写法

前期知识

先来看一下股票题目家族。

一类不限制交易次数；一类交易 k 次。
在这里插入图片描述

股票问题

买卖股票的最佳时机 II

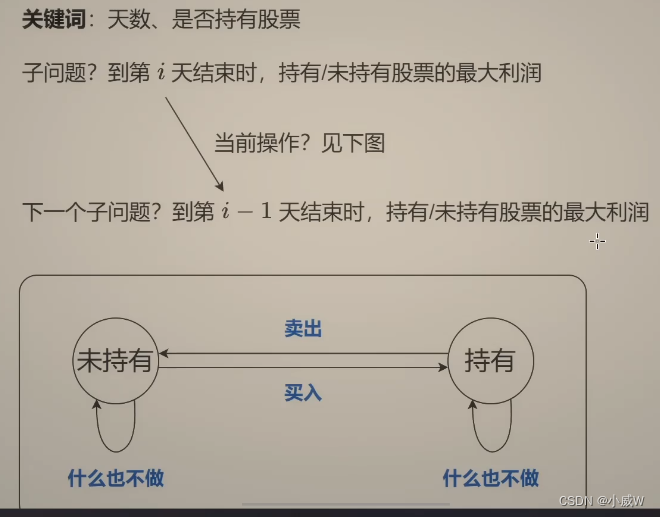
在这里插入图片描述

上图中的转换过程就是状态机。
状态转移方程如下：

定义成两个 dp 数组 buy 和 sell 会更清晰一些。

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[] sell = new int[n], buy = new int[n];
        buy[0] = -prices[0];
        for (int i = 1; i < n; ++i) {
            sell[i] = Math.max(sell[i - 1], buy[i - 1] + prices[i]);
            buy[i] = Math.max(buy[i - 1], sell[i - 1] - prices[i]);
        }
        return sell[n - 1];
    }
}

由于 无后效性 ，因此两个数组可以空间优化成两个变量。

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int sell = 0, buy = -prices[0];
        for (int i = 1; i < n; ++i) {
            int newSell = Math.max(sell, buy + prices[i]);
            buy = Math.max(buy, sell - prices[i]);
            sell = newSell;
        }
        return sell;
    }
}

最佳买卖股票时机含冷冻期

在这里插入图片描述
这是买卖股票的最佳时机 II 的一道变形题，唯一的区别在于，卖出股票之后的第二天不能购买股票。

直接把上一题的代码抄过来进行修改。

由于冷冻期的限制，buy[i] 的状态需要从 sell[i - 2] 转移过来，除此之外没有任何区别了。

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        if (n == 1) return 0;
        int[] sell = new int[n], buy = new int[n];
        buy[0] = -prices[0];
        buy[1] = Math.max(buy[0], -prices[1]);
        sell[1] = Math.max(sell[0], buy[0] + prices[1]);
        for (int i = 2; i < n; ++i) {
            sell[i] = Math.max(sell[i - 1], buy[i - 1] + prices[i]);
            buy[i] = Math.max(buy[i - 1], sell[i - 2] - prices[i]);
        }
        return sell[n - 1];
    }
}

由于循环中的下标开始位置变成了 2，因此前面的初始化过程要写到 buy[1] 和 sell[1] 。

买卖股票的最佳时机 IV

买卖股票的最佳时机 IV
在这里插入图片描述
一个直接的方法就是将 dp 数组再扩展一维：dp[i][j]表示在第 i 天第 j 次交易时买入/卖出的最大收益。
对于每天之间的转移是不变的；每次交易之间的转移，buy 只能从上次交易的 sell 转移而来，sell 从这次交易的 buy 转移而来。（因为一个 buy + sell 是一次完整的交易）

class Solution {
    public int maxProfit(int k, int[] prices) {
        int n = prices.length;
        // dp[i][j]表示在第i天第j次交易时买入/卖出的最大收益
        int[][] buy = new int[n][k], sell = new int[n][k];
        Arrays.fill(buy[0], -prices[0]);    // dp数组初始化
        for (int i = 1; i < n; ++i) {
            // 处理在第i天第0次交易的情况
            buy[i][0] = Math.max(-prices[i], buy[i - 1][0]);
            sell[i][0] = Math.max(sell[i - 1][0], buy[i - 1][0] + prices[i]);
            for (int j = 1; j < k; ++j) {
                buy[i][j] = Math.max(buy[i - 1][j], sell[i - 1][j - 1] - prices[i]);
                sell[i][j] = Math.max(sell[i - 1][j], buy[i - 1][j] + prices[i]);
            }
        }
        return sell[n - 1][k - 1];
    }
}

解读一下

buy[i][j] = Math.max(buy[i - 1][j], sell[i - 1][j - 1] - prices[i]);
sell[i][j] = Math.max(sell[i - 1][j], buy[i - 1][j] + prices[i]);

和买卖股票的最佳时机 II 这道题的代码

sell[i] = Math.max(sell[i - 1], buy[i - 1] + prices[i]);
buy[i] = Math.max(buy[i - 1], sell[i - 1] - prices[i]);

相比，状态转移的第一维下标是相同的。
而每次交易之间的转移，buy 只能从上次交易的 sell 转移而来，sell 从这次交易的 buy 转移而来。（因为一个 buy + sell 是一次完整的交易），这决定了第二维下标的选择。

一维 dp 版本（实际上是去掉了二维 dp 的第一维）

class Solution {
    public int maxProfit(int k, int[] prices) {
        int n = prices.length;
        int[] buy = new int[k], sell = new int[k];
        Arrays.fill(buy, -prices[0]);
        for (int i = 0; i < n; ++i) {
            buy[0] = Math.max(buy[0], -prices[i]);
            sell[0] = Math.max(sell[0], buy[0] + prices[i]);
            for (int j = 1; j < k; ++j) {
                buy[j] = Math.max(buy[j], sell[j - 1] - prices[i]);
                sell[j] = Math.max(sell[j], buy[j] + prices[i]);
            }
        }
        return sell[k - 1];
    }
}

补充：恰好k次 / 至少k次怎么做？

在这里插入图片描述

相关题目练习

买卖股票的最佳时机 https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/
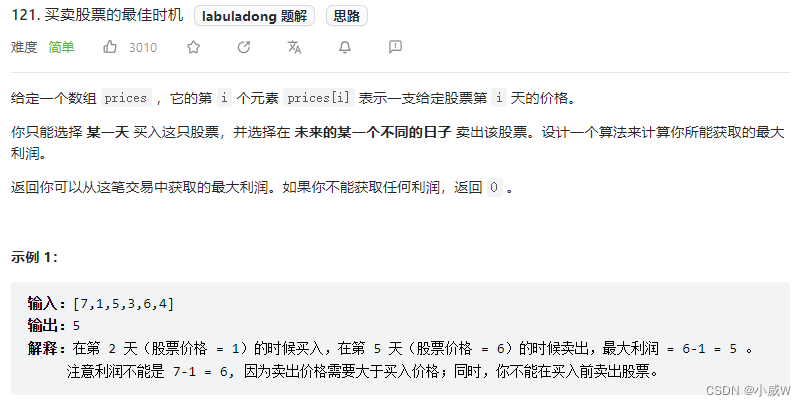
在这里插入图片描述

解法1——状态机DP

我们还是按照上面题目的做法来做，这道题目相当于只能买 1 次股票。

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[] sell = new int[n], buy = new int[n];
        buy[0] = -prices[0];
        for (int i = 1; i < n; ++i) {
            buy[i] = Math.max(buy[i - 1], -prices[i]);
            sell[i] = Math.max(sell[i - 1], buy[i - 1] + prices[i]);
        }
        return sell[n - 1];
    }
}

代码整体几乎和 122. 买卖股票的最佳时机 II 一样，唯一不同的点在于：buy[i] 不能从 sell[i - 1] 转移来了，因为最多只能买一次股票。
对应代码中把 buy[i] = Math.max(buy[i - 1], sell[i - 1] - prices[i]); 改成了 buy[i] = Math.max(buy[i - 1], -prices[i]);。

解法2——贪心

在这里插入图片描述

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length, ans = 0, mn = Integer.MAX_VALUE;
        for (int price: prices) {
            mn = Math.min(mn, price);
            ans = Math.max(ans, price - mn);
        }
        return ans;
    }
}

买卖股票的最佳时机 III https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/

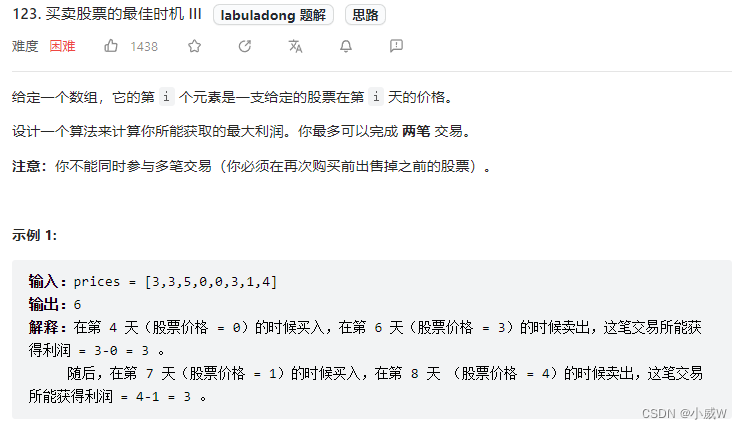
在这里插入图片描述

这道题目很熟悉对吧，其实就是 最多 k 次交易那道题目。（k = 2 时的特例）

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[][] buy = new int[n][2], sell = new int[n][2];
        buy[0][0] = buy[0][1] = -prices[0];
        for (int i = 1; i < n; ++i) {
            buy[i][0] = Math.max(buy[i - 1][0], -prices[i]);
            sell[i][0] = Math.max(sell[i - 1][0], buy[i - 1][0] + prices[i]);
            buy[i][1] = Math.max(buy[i - 1][1], sell[i - 1][0] - prices[i]);
            sell[i][1] = Math.max(sell[i - 1][1], buy[i - 1][1] + prices[i]);
        }
        return sell[n - 1][1];
    }
}

买卖股票的最佳时机含手续费 https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/

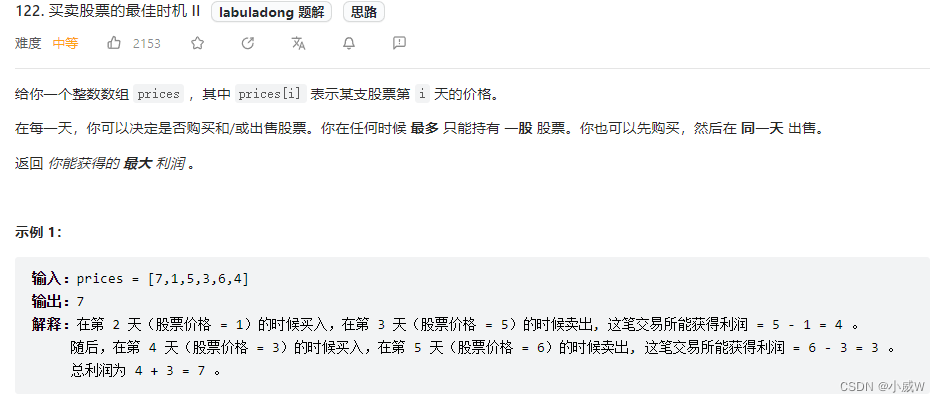
在这里插入图片描述

122. 买卖股票的最佳时机 II 的变形题，只需要修改状态转移部分，在每次购买或卖出股票时加上一个手续费即可。

买入时加上手续费：

class Solution {
    public int maxProfit(int[] prices, int fee) {
        int n = prices.length;
        int sell = 0, buy = -prices[0] - fee;
        for (int i = 1; i < n; ++i) {
            int newSell = Math.max(sell, buy + prices[i]);
            buy = Math.max(buy, sell - prices[i] - fee);
            sell = newSell;
        }
        return sell;
    }
}

卖出时加上手续费：

class Solution {
    public int maxProfit(int[] prices, int fee) {
        int n = prices.length;
        int sell = 0, buy = -prices[0];
        for (int i = 1; i < n; ++i) {
            int newSell = Math.max(sell, buy + prices[i] - fee);
            buy = Math.max(buy, sell - prices[i]);
            sell = newSell;
        }
        return sell;
    }
}

最大子序列交替和 https://leetcode.cn/problems/maximum-alternating-subsequence-sum/

https://leetcode.cn/problems/maximum-alternating-subsequence-sum/

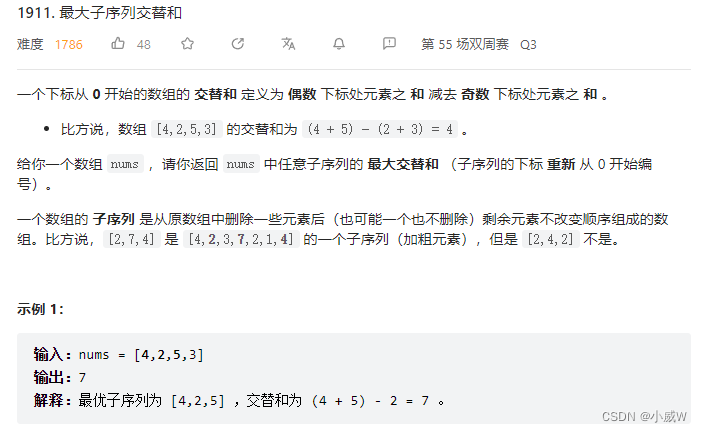
在这里插入图片描述
理解方式1：一个可以先卖出一个股票，再买入的 122. 买卖股票的最佳时机 II 。
理解方式2：按 122. 买卖股票的最佳时机 II 来计算怎么能亏得最多，最后的结果取负号。

理解1写法

class Solution {
    public long maxAlternatingSum(int[] prices) {
        int n = prices.length;
        long sell = prices[0], buy = 0; // 只需要修改初始状态
        for (int i = 1; i < n; ++i) {
            long newSell = Math.max(sell, buy + prices[i]);
            buy = Math.max(buy, sell - prices[i]);
            sell = newSell;
        }
        return sell;
    }
}

理解2写法

class Solution {
    public long maxAlternatingSum(int[] prices) {
        int n = prices.length;
        long sell = 0, buy = -prices[0];
        for (int i = 1; i < n; ++i) {
        	// 从求max变成求min
            long newSell = Math.min(sell, buy + prices[i]);
            buy = Math.min(buy, sell - prices[i]);
            sell = newSell;
        }
        return -buy;	// 亏损最大值取负号
    }
}