Problem - 1625C - Codeforces
火星政府不仅对优化太空飞行感兴趣,还希望改进该行星的道路系统。
火星上最重要的高速公路之一连接着奥林匹克城和西多尼亚的首都Kstolop。在这个问题中,我们只考虑从Kstolop到奥林匹克城的路线,而不考虑相反的路径(即从奥林匹克城到Kstolop的路径)。
从Kstolop到奥林匹克城的公路长度为ℓ 公里。公路上的每个点都有一个坐标x(0≤x≤ℓ),它表示距离Kstolop的公里数。因此,Kstolop位于坐标为0的点,奥林匹克城位于坐标为ℓ的点。
沿途有n个路标,第i个路标设置了限速ai。该限速意味着必须在下一公里内以ai分钟通过,并在遇到沿途下一个路标之前保持有效。起点处(即坐标为0的点)有一个路标,设置了初始限速。
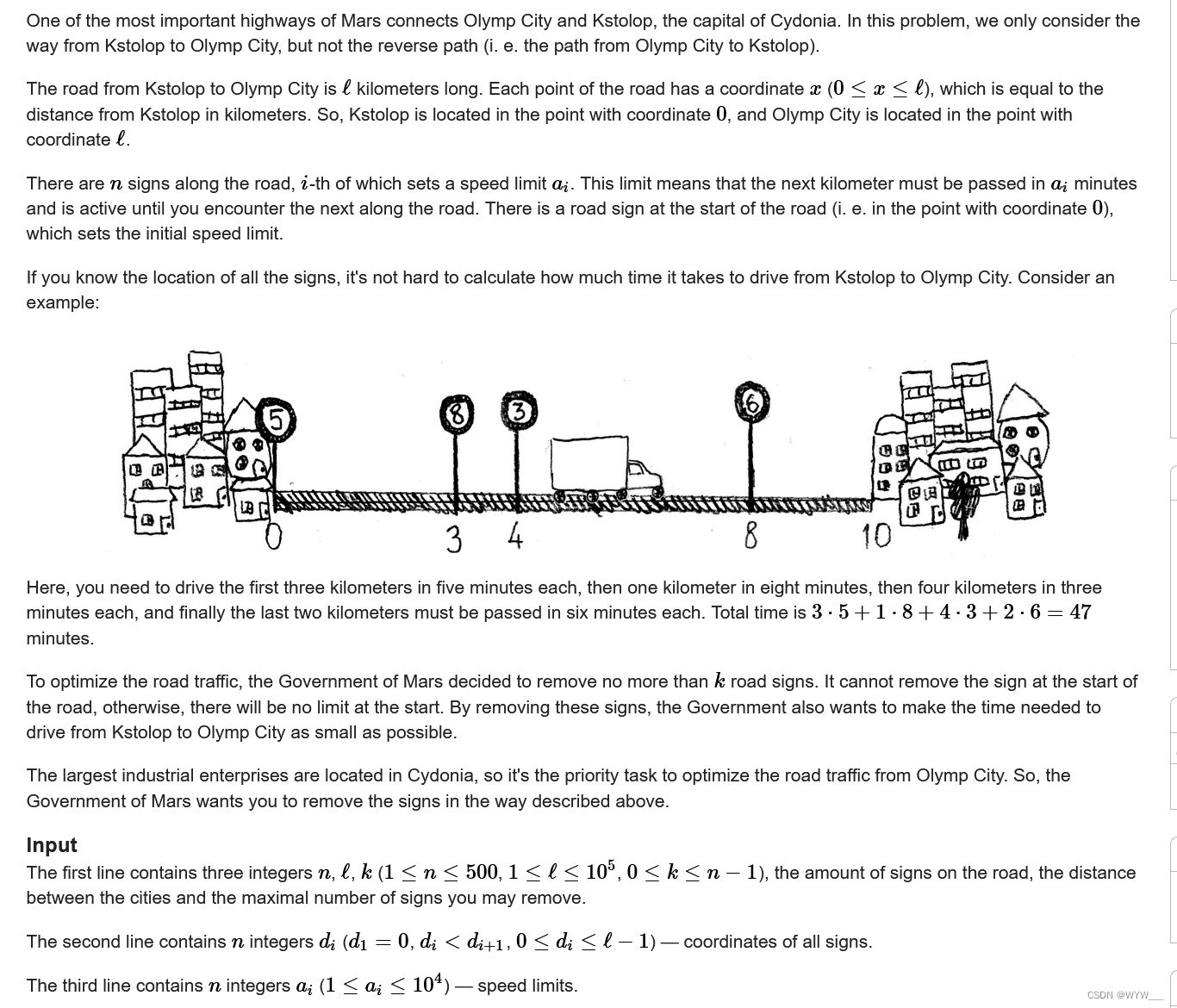
如果你知道所有路标的位置,计算从Kstolop到奥林匹克城所需的时间就不难。考虑一个例子:
在这个例子中,你需要以每分钟5公里的速度驾驶前三公里,然后以每分钟8公里的速度驾驶一公里,接下来以每分钟3公里的速度驾驶四公里,最后两公里必须以每分钟6公里的速度通过。总时间是3⋅5+1⋅8+4⋅3+2⋅6=47 分钟。
为了优化道路交通,火星政府决定最多移除k个路标。它不能移除起点处的路标,否则起点将没有限速。通过移除这些路标,政府还希望使从Kstolop到奥林匹克城所需的时间尽可能短。
最大的工业企业位于西多尼亚,所以优化从奥林匹克城到此地的道路交通是首要任务。因此,火星政府希望你按照上述方式移除路标。
输入:
第一行包含三个整数n、ℓ和k(1≤n≤500,1≤ℓ≤105,0≤k≤n−1),表示道路上的路标数量、城市之间的距离和最多可以移除的路标数。
第二行包含n个整数di(d1=0,di<di+1,0≤di≤ℓ−1),表示所有路标的坐标。
第三行包含n个整数ai(1≤ai≤104),表示限速。
输出:
输出一个整数,表示从Kstolop到奥林匹克城的最小可能时间(以分钟为单位),如果不移除超过k个路标。
Examples
Input
Copy
4 10 0 0 3 4 8 5 8 3 6
Output
Copy
47
Input
Copy
4 10 2 0 3 4 8 5 8 3 6
Output
Copy
38
题解:
由于选k个,无法确定每个位置删除不删除,所以要用三维dp
dp[i][1][j]
代表前i个里面选j个,第i个不删的情况
0代表删的情况
由于路径总长度是l,所以最后加上l,我们下标从0开始
初始化全为最大值,由于初始位置不能删,所以dp[0][1][0] = a[0]*(d[1] - d[0])
对于一个位置不删的情况,转移方程比较好写
由上一个位置转移过来
dp[i][1][j] = min(dp[i - 1][1][j],dp[i - 1][0][j]) + a[i]*(d[i + 1] - d[i]);
对dp[i][0][j]来说,i已经移除了,我们没找到最后一个被移除的路标,所以我们要列举i之前的所有坐标找最后一个没有被移除的坐标l,算出花费时间的最小值
花费的时间是min(dp[ l ][ 1 ][ j - ( i - l )]+a[ l ]*(d[l+1]-d[i+1]));(因为最后一个没有被移除的路标如果是第l个的话,那么从l到i的所有路标都会被移除,那么后面就移除了(i-l)个路标,那么到l这的话是移除了j-(i-l)个路标,
为啥a[ l ]*(d[l+1]-d[i+1]),是d[l + 1],因为我们之前不删的情况,都会考虑后面,一个,已经改变过了,
#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
#define int long long
typedef pair<int,int> PII;
typedef unsigned long long ULL;
const int N = 5e5 + 10;
int mod = 998244353;
int dp[505][2][505];
int d[N];
int a[N];
void solve()
{
int n,x,k;
cin >> n >> x >> k;
d[n] = x;
for(int i = 0;i < n;i++)
{
cin >> d[i];
}
for(int i = 0;i < n;i++)
{
cin >> a[i];
}
memset(dp,0x3f,sizeof dp);
int ans = 1e18;
dp[0][1][0] = a[0]*(d[1] - d[0]);
for(int i = 1;i < n;i++)
{
for(int j = 0;j <= k;j++)
{
dp[i][1][j] = min(dp[i - 1][0][j],dp[i - 1][1][j]) + (a[i])*(d[i + 1] - d[i]);
for(int l = 0;l < i;l++)
{
if(j >= i - l)
{
dp[i][0][j] = min(dp[i][0][j],dp[l][1][j - (i - l)] + (a[l]*(d[i + 1] - d[l + 1])));
}
}
}
}
for(int i = 0;i <= k;i++)
{
ans = min(ans,min(dp[n - 1][0][i],dp[n - 1][1][i]));
}
cout << ans;
}
signed main()
{
ios::sync_with_stdio(0 );
cin.tie(0);cout.tie(0);
int t = 1;
// cin >> t;
while(t--)
{
solve();
}
}