1.概述
所谓排序, 就是使一串记录, 按照其中的某个或某些关键字的大小, 递增或递减的排列起来的操作。 排序算法, 就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视, 尤其是在大量数据的处理方面。 一个优秀的算法可以节省大量的资源。 在各个领域中考虑到数据的各种限制和规范,要得到一个符合实际的优秀算法, 得经过大量的推理和分析。
排序算法稳定性: 假定在待排序的记录序列中, 具有多个相同的元素, 若经过排序, 这些记录的相对次序保持不变, 即在原序列中, r[i]=r[j], 且 r[i]在 r[j]之前, 而在排序后的序列中, r[i]仍在 r[j]之前, 则称这种排序算法是稳定的; 否则称为不稳定的。
时间复杂度: 即从序列的初始状态到经过排序算法的位置交换处理, 得到最终排序好的结果状态的过程所花费的时间度量。 在计算机科学中, 时间复杂性, 又称时间复杂度, 算法的时间复杂度是一个函数, 它定性描述该算法的运行时间。 这是一个代表算法输入值的字符串的长度的函数。 时间复杂度常用O符号表示。
2.冒泡排序
冒泡排序实现原理是把较小元素(较大元素)往后调。通过对相邻元素进行两两比较,根据比较结果将两元素位置对调, 最终达到从小到大或者从大到小的顺序。
冒泡排序的基本思想是: 如按从大到小顺序排序, 将第 1 个元素和第 2 个元素比较,若第 1 个小于第 2 个,则将两个元素位置交换, 反之则不动; 接着再对第 2 个元素和第 3 个元素比较, 若第 2 个小于第 3 个, 则将两个元素位置交换, 反之则不动; 依次类推, 一轮下来则将找到一个最小值放到最末尾。接下来在进行第二轮比较, 则可以找到第二小值放到倒数第二位置, 直到进行 n-1轮比较,即可使数据有序。
冒泡排序时间复杂度: O(n²)。
冒泡排序是一个稳定的排序算法。

#include <stdio.h>
int main()
{
int data[]={4,1,3,6,2,5};
int i=0,j;
int temp;
int count=sizeof(data)/sizeof(int);
for(i=0;i<count-1;i++)//比较轮数
{
for(j=0;j<count-1-i;j++)//每轮比较的次数
{
if(data[j]>data[j+1])
{
temp=data[j];
data[j]=data[j+1];
data[j+1]=temp;
}
}
}
printf("从小到大:");
for(i=0;i<count;i++)
{
printf("%d ",data[i]);
}
printf("\n");
}
2.快速排序
快速排序算法通过多次比较和交换来实现排序,其排序流程如下:
(1)首先设定一个分界值,通过该分界值将数组分成左右两部分。
(2)将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于分界值,而右边部分中各元素都大于或等于分界值。
(3)然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
(4)重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
快速排序(Quick_sort)是对冒泡排序的一种改进,它也是属于冒泡类的方法。
快速排序时间复杂度:O(log2n)。
快速排序是一个不稳定的排序算法。

#include <stdio.h>
void quicksort(int *arr,int first,int end);
int main()
{
int arr[]={3,5,7,1,2,4,6};
quicksort(arr,0,7-1);
int i=0;
for(i=0;i<7;i++)
{
printf("%d ",arr[i]);
}
printf("\n");
return 0;
}
void quicksort(int *arr,int first,int end)
{
if(first>=end)return ;
int i=first;
int j=end;
int pivot=arr[i];
int cnt=0;
while(1)
{
while(arr[i]<=pivot && i<end)i++;//从前往后找大于pivot的数
while(arr[j]>=pivot && j>first)j--;//从后往前找小于pivot的数据
if(i>=j)break;
//交换位置
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
arr[first]=arr[j];
arr[j]=pivot;
quicksort(arr,0,j);//对前半部分排序
quicksort(arr,j+1,end);//对后半部分排序
}
3.插入排序
插入排序,一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排序方法,它的实现原理是将一个元素插入到一个有序列表中。其实现过程可以通过两层循环,外层循环控制有序列表的数量,内层循环是判断新元素,将新元素插入到有序列表中。
- 时间复杂度:
在插入排序中,当待排序数组是有序时,此时为最优情况,只需当前数跟前一个数比较一下,这时一共需要比较N- 1次,时间复杂度为O(N)。
最坏的情况是待排序数组是逆序的,此时需要比较次数最多,总次数记为:1+2+3+…+N-1,所以,插入排序最坏情况下的时间复杂度为O(N²)。
插入排序适用于已经有部分数据有序,并且有序数列越大越好。一般在数据规模大于1000的场合下不建议使用插入排序。
插入排序是一个不稳定的排序算法。

#include <stdio.h>
int main()
{
char buff[]={3,5,7,1,2,64,6};
int count=sizeof(buff)/sizeof(char);
int i,j;
int temp;
for(i=1;i<count;i++)
{
for(j=i;j>0;j--)
{
if(buff[j]>buff[j-1])
{
temp=buff[j];
buff[j]=buff[j-1];
buff[j-1]=temp;
}
}
}
for(i=0;i<count;i++)
{
printf("%d ",buff[i]);
}
printf("\n");
}
4.希尔排序
希尔排序(Shell’s Sort)是插入排序的一种,又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。该方法因 D.L.Shell于1959年提出而得名。
希尔排序是把要排序的元素进行分组插入排序,把元素的分组数作为循环轮数,分组数量一般设置为log2N(N为成员个数)。每完成一轮,分组数量减半,直到组数为1,即整个元素分成一组,即排序完成。
希尔排序是按照不同步长对元素进行插入排序,当刚开始元素很无序的时候,步长最大,所以插入排序的元素个数很少,速度很快;当元素基本有序了,步长很小,插入排序对于有序的序列效率很高。所以,希尔排序的时间复杂度会比O(N²)好一些。
希尔排序是一个稳定的排序算法。

#include <stdio.h>
void shellSort(int *arr,int count)
{
int gap=0;
int temp;
int i=0,j=0;
for(gap=count>>1;gap>0;gap>>=1)
{
for(i=gap;i<count;i++)
{
temp=arr[i];
j=i-gap;
while(j>=0 && arr[j]<temp)
{
arr[j+gap]=arr[j];
j-=gap;
}
arr[j+gap]=temp;
}
}
}
int main()
{
int arr[]={1,2,3,4,5,6,7,8};
int count=sizeof(arr)/sizeof(int);
shellSort(arr,count);
printf("从大到小排序:\n");
for(int i=0;i<count;i++)
{
printf("%d ",arr[i]);
}
printf("\n");
}
5.选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。
选择排序时间复杂度都是O(n²)。
选择排序是一个不稳定的排序算法。
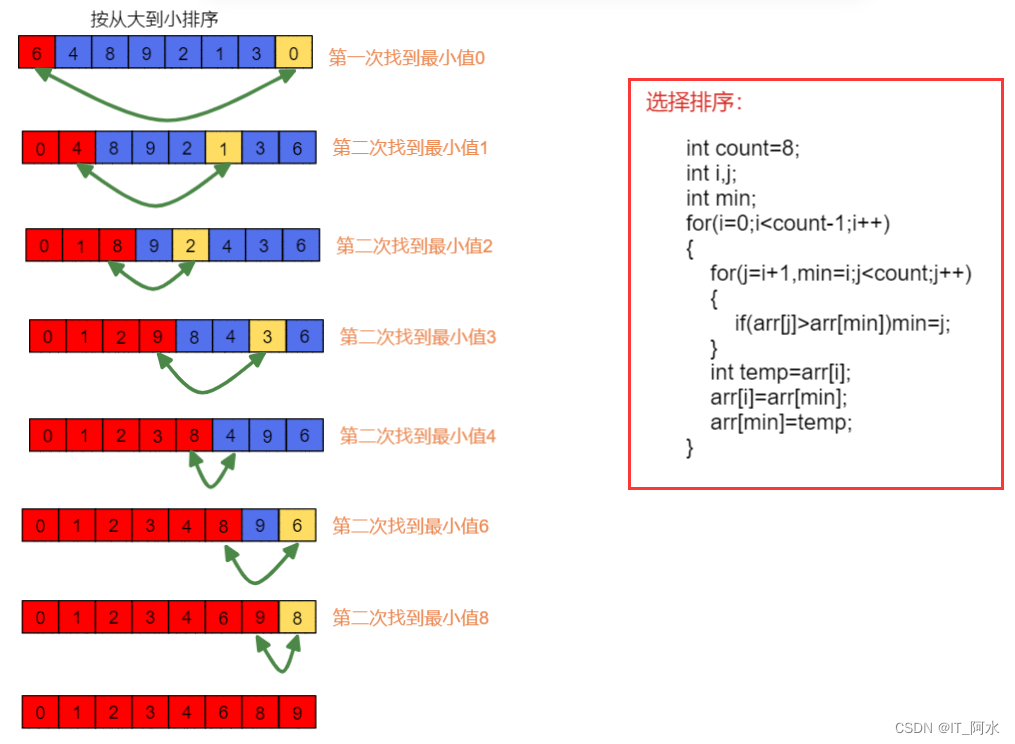
void SelectSort(int *arr,int count)
{
int i,j;
int temp;
int min;
for(i=0;i<count-1;i++)
{
min=i;
for(j=i+1;j<count;j++)
{
//找到最小的下下标
if(arr[j]<arr[min])min=j;
}
temp=arr[i];
arr[i]=arr[min];
arr[min]=temp;
}
}
void main(){
int arr[] = {6,4,8,9,2,3,1,0};
int count=sizeof(arr)/sizeof(int);
SelectSort(arr,count);
int i=0;
printf("排序结果:");
for(i=0;i<count;i++)
{
printf("%d ",arr[i]);
}
printf("\n");
}