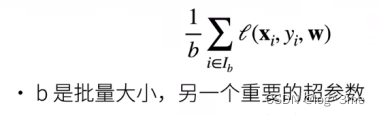- 点击跳转专栏=>Unity3D特效百例
- 点击跳转专栏=>案例项目实战源码
- 点击跳转专栏=>游戏脚本-辅助自动化
- 点击跳转专栏=>Android控件全解手册
- 点击跳转专栏=>Scratch编程案例
- 点击跳转=>软考全系列
- 点击跳转=>蓝桥系列
👉关于作者
专注于Android/Unity和各种游戏开发技巧,以及各种资源分享(网站、工具、素材、源码、游戏等)
有什么需要欢迎底部卡片私我,获取更多支持,交流让学习不再孤单。

👉实践过程
需要所有整理的文档可底部卡片联系我,直接发压缩包。
😜地宫取宝
问题描述
X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。
地宫的入口在左上角,出口在右下角。
小明被带到地宫的入口,国王要求他只能向右或向下行走。
走过某个格子时,如果那个格子中的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它(当然,也可以不拿)。
当小明走到出口时,如果他手中的宝贝恰好是k件,则这些宝贝就可以送给小明。
请你帮小明算一算,在给定的局面下,他有多少种不同的行动方案能获得这k件宝贝。
输入格式
输入一行3个整数,用空格分开:n m k (1<=n,m<=50, 1<=k<=12)
接下来有 n 行数据,每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值
输出格式
要求输出一个整数,表示正好取k个宝贝的行动方案数。该数字可能很大,输出它对 1000000007 取模的结果。
样例输入
2 2 2
1 2
2 1
样例输出
2
样例输入
2 3 2
1 2 3
2 1 5
样例输出
14
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;
public class Main
{
private static StreamTokenizer tokenizer = new StreamTokenizer(
new InputStreamReader(System.in));
private static PrintWriter outWriter = new PrintWriter(
new OutputStreamWriter(System.out));
private static int n, m, k;
private static int[][] table;
private static final int MOD = 1000000007;
private static long[][][][] state;
private static long dfs(int i, int j, int num, int max)
{
if (state[i][j][num][max] != -1)
return state[i][j][num][max];
long currentAns = 0;
if (i == n - 1 && j == m - 1)
{
if (num == k || max < table[i][j] && num + 1 == k)
currentAns++;
state[i][j][num][max] = currentAns;
return currentAns;
}
if (i + 1 < n)
{
currentAns += dfs(i + 1, j, num, max);
if (max < table[i][j] && num + 1 <= k)
currentAns += dfs(i + 1, j, num + 1, table[i][j]);
}
if (j + 1 < m)
{
currentAns += dfs(i, j + 1, num, max);
if (max < table[i][j] && num + 1 <= k)
currentAns += dfs(i, j + 1, num + 1, table[i][j]);
}
state[i][j][num][max] = currentAns;
return currentAns;
}
public static void main(String[] args) throws Exception
{
tokenizer.nextToken();
n = (int) tokenizer.nval;
tokenizer.nextToken();
m = (int) tokenizer.nval;
tokenizer.nextToken();
k = (int) tokenizer.nval;
table = new int[n][m];
state = new long[n][m][k + 1][14];
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
for (int t = 0; t <= k; t++)
Arrays.fill(state[i][j][t], -1);
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
{
tokenizer.nextToken();
table[i][j] = (int) tokenizer.nval;
table[i][j]++;
}
long ret = dfs(0, 0, 0, 0);
outWriter.println(ret % MOD);
outWriter.flush();
}
}
😜斐波那契
问题描述
斐波那契数列大家都非常熟悉。它的定义是:
f(x) = 1 … (x=1,2)
f(x) = f(x-1) + f(x-2) … (x>2)
对于给定的整数 n 和 m,我们希望求出:
f(1) + f(2) + … + f(n) 的值。但这个值可能非常大,所以我们把它对 f(m) 取模。
公式如下图
但这个数字依然很大,所以需要再对 p 求模。
输入格式
输入为一行用空格分开的整数 n m p (0 < n, m, p < 10^18)
输出格式
输出为1个整数,表示答案
样例输入
2 3 5
样例输出
0
样例输入
15 11 29
样例输出
25

import java.math.BigInteger;
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc=new Scanner(System.in);
long n,m;
n=sc.nextLong();
m=sc.nextLong();
BigInteger p=sc.nextBigInteger(),fn,fm;
if(n+2>m)
{
fm=think(m,null);
fn=think(n+2,fm).subtract(new BigInteger("1"));
System.out.println(fn.remainder(fm).remainder(p));
}
else
{
fn=think(n+2,p).subtract(new BigInteger("1"));
System.out.println(fn.remainder(p));
}
}
private static BigInteger think(long m,BigInteger mod) {
// TODO Auto-generated method stub
BigInteger a1=new BigInteger("1"),a2=new BigInteger("1"),x[][];
if(m==1)return a1;
else if(m==2)return a2;
else
{
x=new BigInteger[2][2];
x[0][0]=new BigInteger("1");
x[0][1]=new BigInteger("1");
x[1][0]=new BigInteger("1");
x[1][1]=new BigInteger("0");
x=doublex(x,m-2,mod);
return x[0][0].add(x[0][1]);
}
}
private static BigInteger[][] doublex(BigInteger[][] x, long n,BigInteger mod) {
// TODO Auto-generated method stub
BigInteger x2[][];
x2=new BigInteger[2][2];
if(n==1)return x;
else
{
if(n%2==1)return cheng(doublex(cheng(x,x,mod),n/2,mod),x,mod);
else return doublex(cheng(x,x,mod),n/2,mod);
}
}
private static BigInteger[][] cheng(BigInteger[][] x, BigInteger[][] y,BigInteger mod) {
// TODO Auto-generated method stub
BigInteger z[][];
z=new BigInteger[2][2];
if(mod!=null)
{
z[0][0]=x[0][0].multiply(y[0][0]).add(x[1][0].multiply(y[0][1])).remainder(mod);
z[0][1]=x[0][0].multiply(y[0][1]).add(x[0][1].multiply(y[1][1])).remainder(mod);
z[1][0]=x[1][0].multiply(y[0][0]).add(x[1][1].multiply(y[1][0])).remainder(mod);
z[1][1]=x[1][0].multiply(y[0][1]).add(x[1][1].multiply(y[1][1])).remainder(mod);
return z;
}
z[0][0]=x[0][0].multiply(y[0][0]).add(x[1][0].multiply(y[0][1]));
z[0][1]=x[0][0].multiply(y[0][1]).add(x[0][1].multiply(y[1][1]));
z[1][0]=x[1][0].multiply(y[0][0]).add(x[1][1].multiply(y[1][0]));
z[1][1]=x[1][0].multiply(y[0][1]).add(x[1][1].multiply(y[1][1]));
return z;
}
}
😜波动数列
问题描述
观察这个数列:
1 3 0 2 -1 1 -2 …
这个数列中后一项总是比前一项增加2或者减少3。
栋栋对这种数列很好奇,他想知道长度为 n 和为 s 而且后一项总是比前一项增加a或者减少b的整数数列可能有多少种呢?
输入格式
输入的第一行包含四个整数 n s a b,含义如前面说述。
输出格式
输出一行,包含一个整数,表示满足条件的方案数。由于这个数很大,请输出方案数除以100000007的余数。
样例输入
4 10 2 3
样例输出
2
样例说明
这两个数列分别是2 4 1 3和7 4 1 -2。
数据规模和约定
对于10%的数据,1<=n<=5,0<=s<=5,1<=a,b<=5;
对于30%的数据,1<=n<=30,0<=s<=30,1<=a,b<=30;
对于50%的数据,1<=n<=50,0<=s<=50,1<=a,b<=50;
对于70%的数据,1<=n<=100,0<=s<=500,1<=a, b<=50;
对于100%的数据,1<=n<=1000,-1,000,000,000<=s<=1,000,000,000,1<=a, b<=1,000,000。
public class Main {
public static void main(String[] args) {
int mod = 100000007;
int n, s, a, b, i, j, t;
int x[][] = new int[1001][1001];
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
s = sc.nextInt();
a = sc.nextInt();
b = sc.nextInt();
b %= n;
b *= -1;
while (b < 0)
b += n;
a %= n;
s %= n;
while (s < 0)
s += n;
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
x[i][j] = 0;
x[1][a] = x[1][b] = 1;
for (i = 1; i < n - 1; i++)
for (j = 0; j < n; j++) {
t = (j + a * (i + 1)) % n;
x[i + 1][t] += x[i][j];
x[i + 1][t] %= mod;
t = (j + b * (i + 1)) % n;
t %= n;
x[i + 1][t] += x[i][j];
x[i + 1][t] %= mod;
}
System.out.printf("%d\n", x[n - 1][s]);
}
}
😜小朋友排队
问题描述
n 个小朋友站成一排。现在要把他们按身高从低到高的顺序排列,但是每次只能交换位置相邻的两个小朋友。
每个小朋友都有一个不高兴的程度。开始的时候,所有小朋友的不高兴程度都是0。
如果某个小朋友第一次被要求交换,则他的不高兴程度增加1,如果第二次要求他交换,则他的不高兴程度增加2(即不高兴程度为3),依次类推。当要求某个小朋友第k次交换时,他的不高兴程度增加k。
请问,要让所有小朋友按从低到高排队,他们的不高兴程度之和最小是多少。
如果有两个小朋友身高一样,则他们谁站在谁前面是没有关系的。
输入格式
输入的第一行包含一个整数n,表示小朋友的个数。
第二行包含 n 个整数 H1 H2 … Hn,分别表示每个小朋友的身高。
输出格式
输出一行,包含一个整数,表示小朋友的不高兴程度和的最小值。
样例输入
3
3 2 1
样例输出
9
样例说明
首先交换身高为3和2的小朋友,再交换身高为3和1的小朋友,再交换身高为2和1的小朋友,每个小朋友的不高兴程度都是3,总和为9。
数据规模和约定
对于10%的数据, 1<=n<=10;
对于30%的数据, 1<=n<=1000;
对于50%的数据, 1<=n<=10000;
对于100%的数据,1<=n<=100000,0<=Hi<=1000000。
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main{
static int N = 100010;
static int MAX = 1000100;
static int[] C = new int[MAX];
static int[] S = new int[MAX];
static int[] b = new int[N];
static long[] total = new long[N];
static long ans;
static int[] num = new int[N];
static int T, s, t, i, j;
static int Lowbit(int x) {
return x & (-x);
}
static void add(int pos, int num, int[] P) {
while (pos <= MAX) {
P[pos] += num;
pos += Lowbit(pos);
}
}
static int Sum(int end, int[] P) {
int cnt = 0;
while (end > 0) {
cnt += P[end];
end -= Lowbit(end);
}
return cnt;
}
static void init() {
total[0] = 0;
for (int i = 1; i < N; ++i) {
total[i] = total[i - 1] + i;
}
}
public static void main(String[] args) throws IOException {
init();
BufferedReader buf = new BufferedReader(
new InputStreamReader(System.in));
T = Integer.parseInt(buf.readLine());
String[] str = buf.readLine().split(" ");
for (int j = 0; j < T; j++) {
num[j] = Integer.parseInt(str[j]);
add(num[j] + 1, 1, C);
b[j] = j - Sum(num[j], C);
b[j] -= Sum(num[j] + 1, C) - Sum(num[j], C) - 1;
}
ans = 0;
for (int j = T - 1; j > -1; --j) {
add(num[j] + 1, 1, S);
b[j] += Sum(num[j], S);
ans += total[b[j]];
}
System.out.println(ans);
}
}
👉其他
📢作者:小空和小芝中的小空
📢转载说明-务必注明来源:https://zhima.blog.csdn.net/
📢这位道友请留步☁️,我观你气度不凡,谈吐间隐隐有王者霸气💚,日后定有一番大作为📝!!!旁边有点赞👍收藏🌟今日传你,点了吧,未来你成功☀️,我分文不取,若不成功⚡️,也好回来找我。
温馨提示:点击下方卡片获取更多意想不到的资源。