n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
示例 1:
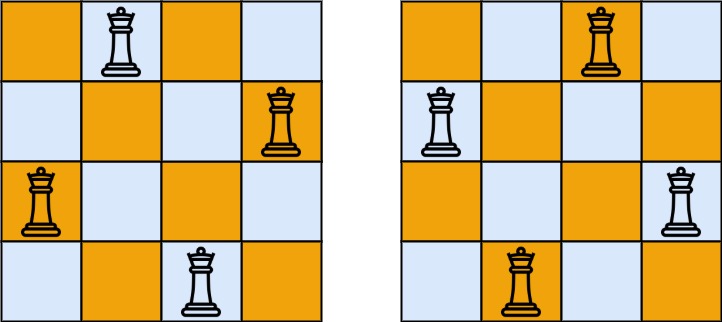
输入:n = 4
输出:2
解释:如上图所示,4 皇后问题存在两个不同的解法。示例 2:
输入:n = 1
输出:1提示:
1 <= n <= 9解题思路:
Java代码
class Solution {
public int totalNQueens(int n) {
// dp[i] : i行上的皇后放在哪一列上, 并且默认i之前的行都已经填好了
int[] dp = new int[n];
for(int i=0; i<n; i++){
dp[i] = -1;
}
return process(dp, 0);
}
// 函数功能:递归函数
// dp[i] : i行上的皇后放在哪一列上, 并且默认i之前的行都已经填好了
// row : 当前来到row行
public int process(int[] dp, int row){
// 当前来到最后一行,则找到一种合法的
if(row==dp.length){
return 1;
}
// 计数
int cnt = 0;
for(int j=0; j<dp.length; j++){
// 判断每一个列位置是否合法
if(check(dp, row, j)){
// row 行的皇后放在j位置
dp[row] = j;
// 递归
cnt += process(dp, row+1);
// 回溯之前的状态
dp[row] = -1;
}
}
return cnt;
}
// 函数功能:判断当前位置是否合法
// dp[i] : i行上的皇后放在哪一列上, 并且默认i之前的行都已经填好了
// i : 当前来到i行
// j : 当前尝试j列
public boolean check(int[] dp, int i, int j){
// 判断该位置是否会和之前的每一行填写的位置发生冲突
for(int row=0; row<i; row++){
// 同列、同斜线则不合法
if(dp[row]==j||(row+dp[row]==i+j)||(row-dp[row]==i-j)){
return false;
}
}
return true;
}
}
Python代码
class Solution(object):
def totalNQueens(self, n):
"""
:type n: int
:rtype: int
"""
# dp[i] : i行上的皇后放在哪一列上, 并且默认i之前的行都已经填好了
dp = [-1 for _ in range(n)]
return self.process(dp, 0)
# 函数功能:递归函数
# dp[i] : i行上的皇后放在哪一列上, 并且默认i之前的行都已经填好了
# row : 当前来到row行
def process(self, dp, row):
# 当前来到最后一行,则找到一种合法的
if row == len(dp):
return 1
# 计数
cnt = 0
for j in range(len(dp)):
# 判断每一个列位置是否合法
if self.check(dp, row, j):
# row 行的皇后放在j位置
dp[row] = j
# 递归
cnt += self.process(dp, row + 1)
# 回溯之前的状态
dp[row] = -1
return cnt
# 函数功能:判断当前位置是否合法
# dp[i] : i行上的皇后放在哪一列上, 并且默认i之前的行都已经填好了
# i : 当前来到i行
# j : 当前尝试j列
def check(self, dp, i, j):
# 判断该位置是否会和之前的每一行填写的位置发生冲突
for row in range(i):
# 同列、同斜线则不合法
if dp[row] == j or (row + dp[row] == i + j) or (row - dp[row] == i - j):
return False
return True