1.MySQL索引存储结构(六种)

Hash结构
Hash本身是一个函数，又被称为散列函数，它可以帮助我们大幅提升检索数据的效率。
Hash算法是通过某种确定性的算法(比如MD5，SHA1，SHA2，SHA3) 将输入转变为输出。`相同的输入永远可以得到相同的输出`，假设输入内容有微小偏差，在输出中通常会有不同的结果。
举例：如果你想验证两个文件是否相同，那么你不需要把两份文件直接拿来比对，只需要让对方把Hash函数计算得到的结果告诉你即可，然后在本地同样对文件进行Hash函数的运算，最后通过比较两个Hash函数的结果是否相同，就可以知道这两个文件是否相同。
加速查找速度的数据结构，常见的有两类：
(1)树，例如平衡二叉搜索数，查询/插入/修改/删除的平均时间复杂度都是O(log2N);
(2)哈希，例如HashMap，查询/插入/修改/删除的平均时间复杂度都是O(1);
采用Hash进行检索效率非常高，基本上一次检索就可以找到数据，而B+树需要自顶向下依次查找，多次访问节点才能找到数据，中间需要多次I/O操作，从效率来说Hash比B+树更快。
在哈希的方式下，一个元素k处于h(k)中，即利用哈希函数h，根据关键词k计算出槽的位置。函数h将关键字域映射到哈希表T[0...m-1]的槽位上。
哈希函数h有可能将两个不同的关键字映射到相同的位置，这叫碰撞，在数据库中一般采用链接法来解决。在链接法中，将散列到同一槽位的元素放在一个链表中。

二叉树
如果我们利用二叉树作为索引结构，那么磁盘的IO次数和索引树的高度是相关的。
为了提高查询效率，就需要减少磁盘IO数。为了减少磁盘IO的次数，就需要尽量降低树的高度，需要把原来“廋高”的树结构变的“矮胖”，树的每层的分叉越多越好。

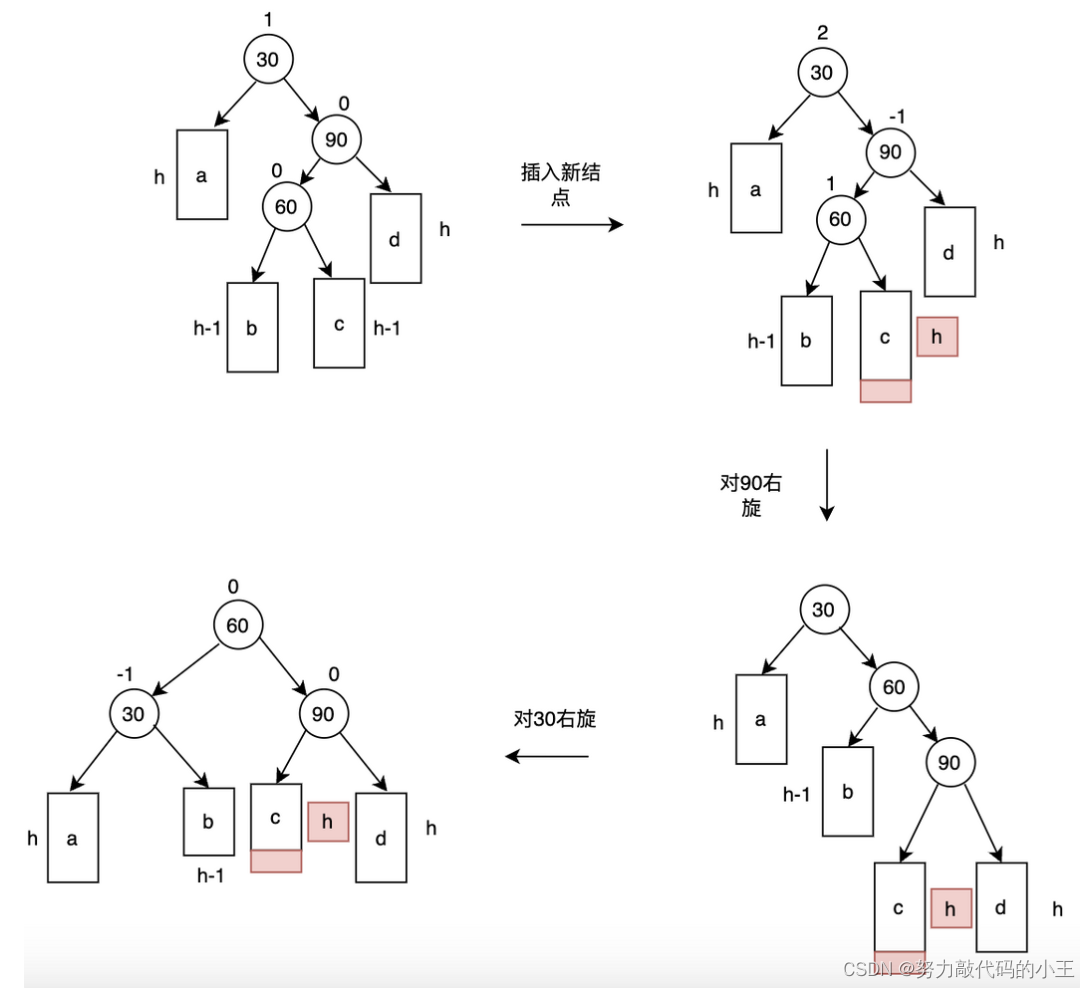
AVL树
为了解决上面二叉查找树退化成链表的问题，人们提出了平衡二叉搜索树(Balanced Binary Tree),又称为AVL树(有别于AVL算法)，它在二叉搜索树的基础上增加了约束，具有以下性质：
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
解决二叉树数据有序时出现的线性插入树太深问题，树的深度会明显降低，极大提高性能，但是当数据量很大时，一般mysql中一张表达到3-5百万条数据是很普遍的，因此平衡二叉树的深度还是非常大，mysql读取时还是会消耗大量IO，不仅如此，计算从磁盘读取数据时以页(4KB)为单位的,及每次读取4096byte。平衡二叉树每个节点只保存了一个关键字（如int即4byte），浪费了4092byte，极大的浪费了读取空间。
你能看到此时树的高度降低了，当数据量N大的时候，以及树的分叉数M大的时候，M叉树的高度会远小于二叉树的高度(M>2)。所以，我们需要把树从“瘦高"变"矮胖”。

B-树
解决平衡二叉树树深度的问题，解决了平衡二叉树读取消耗大量内存空间的问题。因为B-树每个节点可以存放多个关键字，最大限度的利用了从磁盘读取的内存空间，单节点存放多个关键字同时也大大减少了树的深度。极大的提高了mysql的查询性能。但是B-树还是有缺点，B-树对有范围查找的查询（如age>20）时采用的还是中序排序法，因此也需要多遍历，并且查询性能不稳定，比如查询（select * from table where id = 222 和 select * from table where id = 223）时在查询效率（耗时）上可能会存在一定的差别，因为B-树还是将关键字，这里为id，存放在根节点和叶节点的，如果运气好，可能id=222这个关键字就在第一个节点，消耗一次IO就找到了，而id=223可能在叶节点，需要消耗3次IO才能找到。因此B-树对同一条sql语句的查询性能可能会有很大影响（确实感觉有点扯，但是事实时这样）任何一个关键字出现且只出现在一个结点中，数据不一定在子节点上，也可能是父节点，交叉节点等等

B+树
将关键字全部存放在叶子节点(查询更稳定，同一条mysql语句执行效率时相同的，都会消耗3次IO)，将相邻叶子节点的地址保存起来（相比于B-树，对于mysql的范围查找不用再使用中序查找，而是可以直接快读获取到。）

红黑树
树的高度随着数据量增加而增加，IO代价高。

总结如下：
hash：虽然可以快速定位，但是没有顺序，IO复杂度高。
二叉树：树的高度不均匀，不能自平衡，查找效率跟数据有关（树的高度），并且IO代价高。
红黑树：树的高度随着数据量增加而增加，IO代价高。
B-Tree： 矮胖型的树，IO效率相对其他要高，在范围查询时，需要获取所有节点进行遍历，效率相对低下
B+Tree对比B-Tree：数据都在叶子节点上，并且增加了顺序访问指针，每个叶子节点都指向相邻的叶子节点的地址。相比B-Tree来说，进行范围查找时只需要查找两个节点，进行遍历即可。而B-Tree需要获取所有节点，相比之下B+Tree效率更高。

所以说：mysql索引结构默认使用B+Tree，而不是hash，二叉树和红黑树

2.on和where的区别

on是先筛选后关联，where是先关联后筛选
1、on条件是在生成临时表时使用的条件，它不管on中的条件是否为真，都会返回左边表中的记录。
2、where条件是在临时表生成好后，再对临时表进行过滤的条件。这时已经没有left join的含义（必须返回左边表的记录）了，条件不为真的就全部过滤掉。

3.mysql是怎么查重的？(重点掌握3种，distinct，group by，row_number)

1.使用 DISTINCT 关键字：SELECT DISTINCT col1, col2 FROM table1; 该语句会选出表table1中col1和col2不重复的元组。

2.使用 GROUP BY 及聚合函数：SELECT col1, COUNT(col2) FROM table1 GROUP BY col1; 该语句会选出表table1中，以col1为基础，同时统计col2各值共有多少项的查询结果。

3.使用 UNION 关键字：SELECT col1 FROM table1 UNION SELECT col1 FROM table2; 该语句会选出表table1和table2中col1不重复的项，并把它们合并成一个数据集。

4.使用子查询：SELECT * FROM table1 WHERE col1 NOT IN (SELECT col1 FROM table2); 该语句会从表table1中选出col1与表table2中重复的项目剩余部分。

5.使用 JOIN 子句：SELECT * FROM table1 LEFT JOIN table2 ON table1.col1 = table2.col1 WHERE table2.col1 IS NULL; 该语句会找出两者之间的不同之处。除此之外，还有一些其他的方法可用于去重，如:

6.使用 EXISTS 和 NOT EXISTS 操作符：SELECT * FROM table1 t1 WHERE NOT EXISTS (SELECT * FROM table1 t2 WHERE t2.col1 = t1.col1 AND t2.id < t1.id); 该语句会选出col1不重复的行，并且只保留id最小的项。

7.使用 GROUP_CONCAT 和 FIND_IN_SET 函数：SELECT col1, GROUP_CONCAT(col2) AS col2_list FROM table1 GROUP BY col1 HAVING FIND_IN_SET('val', col2_list) = 0; 该语句会选出表table1中col1不重复的项，同时以逗号分隔符将它们对应的col2值合并成一个字符串，并检查该字符串中是否包含指定的关键字。

8.使用临时表和 INSERT INTO SELECT 语句： CREATE TEMPORARY TABLE tmp_table SELECT DISTINCT * FROM table1; SELECT * FROM tmp_table; 该语句会创建一个临时表tmp_table，将去重后的结果插入其中，然后从该临时表中查询数据。需要注意的是，该方法可能会影响性能和内存消耗。

9.使用子查询和LIMIT：SELECT col1 FROM table1 GROUP BY col1 HAVING COUNT(*) > 1 UNION SELECT col1 FROM table1 LIMIT 1; 该语句首先会找出表table1中col1重复的项,然后再将结果和第一项合并输出。

10.使用 PARTITION 分区：SELECT DISTINCT col1 FROM table1 PARTITION(partition_name);

11.使用ROW_NUMBER() OVER (PARTITION BY 去重字段 ORDER BY 排序字段)语法:  SELECT a.* FROM （  SELECT   ROW_NUMBER() OVER (PARTITION BY ID, item_no ORDER BY date desc ) as row_number,ID,item_no,date     FROM    table1) a WHERE   a.row_number = 1;

12.使用EXISTS（或NOT EXISTS)函数

在这里插入图片描述