gitee仓库：https://gitee.com/WangZihao64/data-structure-and-algorithm/tree/master/avl

有如下一棵树(采用加入左结点平衡因子-1，加入右结点平衡因子+1的方式)：

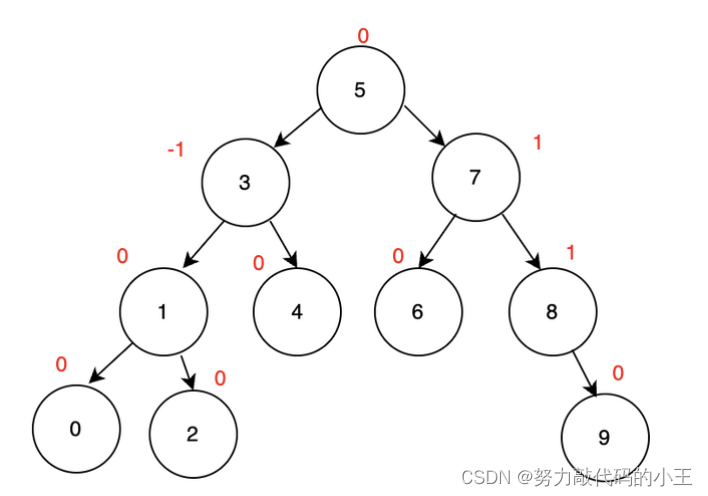
插入有以下几种情况：

1.平衡因子变为2

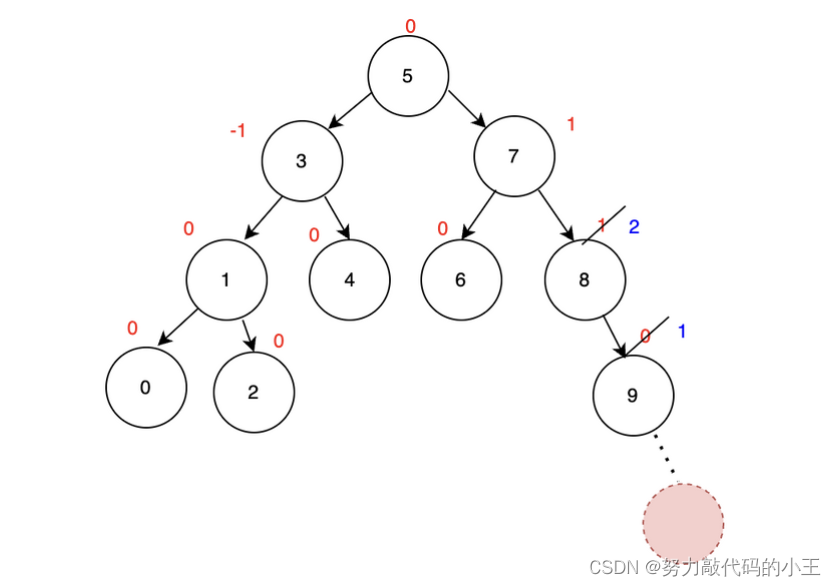
2.平衡因子变为0

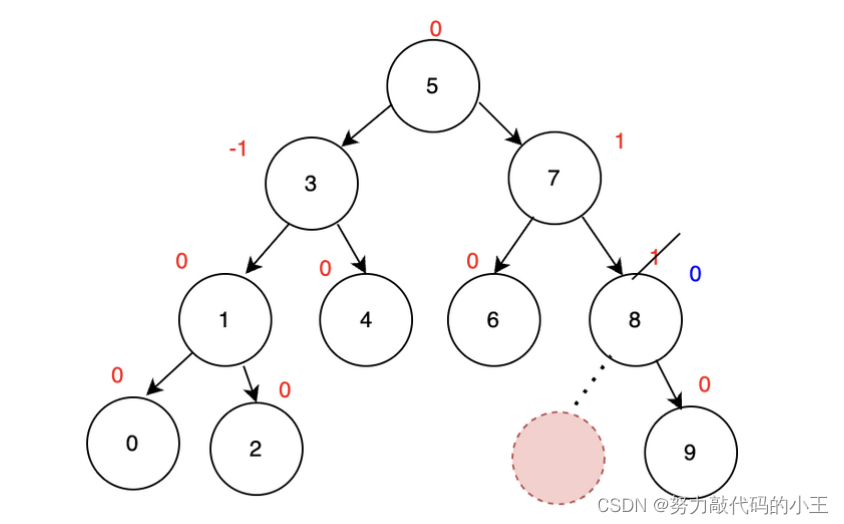
3.平衡因子需要向上延伸（最多可延伸至父结点）

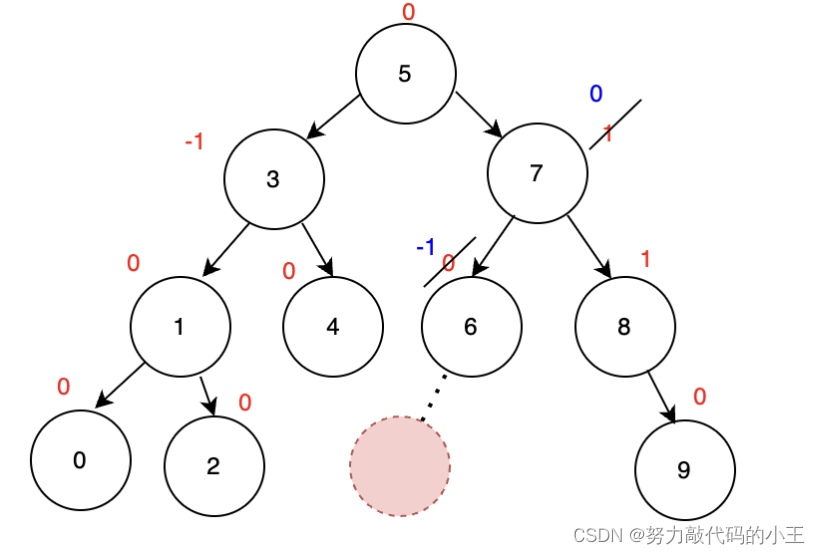
插入和二叉搜索树一样，平衡因子的更新规律如上图

bool Insert(const pair<K,V>& kv)
    {
        if(_root== nullptr)
        {
            _root=new Node(kv);
            return true;
        }
        Node* cur=_root;
        Node* parent=nullptr;
        while(cur)
        {
            if(cur->_kv.first>kv.first)
            {
                parent=cur;
                cur=cur->left;
            }
            else if(cur->_kv.first<kv.first)
            {
                parent=cur;
                cur=cur->right;
            }
            //遇到相同的值，返回false
            else
            {
                return false;
            }
        }
        cur=new Node(kv);
        if(kv.first>parent->_kv.first)
        {
            parent->right=cur;
            cur->parent=parent;
        }
        else
        {
            parent->left=cur;
            cur->parent=parent;
        }
        //parent最多可以走到根节点
        while(parent)
        {
            //parent的左孩子，_bf-1
            //否则_bf+1
            if(parent->left==cur)
            {
                --parent->_bf;
            }
            else if(parent->right==cur)
            {
                ++parent->_bf;
            }
            //parent如果是0，表明是平衡的，不需要做任何操作，直接退出
            if(parent->_bf==0)
            {
                break;
            }
            else if(parent->_bf==-1||parent->_bf==1)
            {
                //如果不平衡，也会影响到父节点的_bf
                cur=parent;
                parent=parent->parent;
            }
            //如果是2/-2就需要特殊处理
            else if(parent->_bf==2||parent->_bf==-2)
            {
                
            }
        }
        return true;
    }

特殊处理有4中情况

• 新节点插入较高左子树的左侧—左左：右单旋

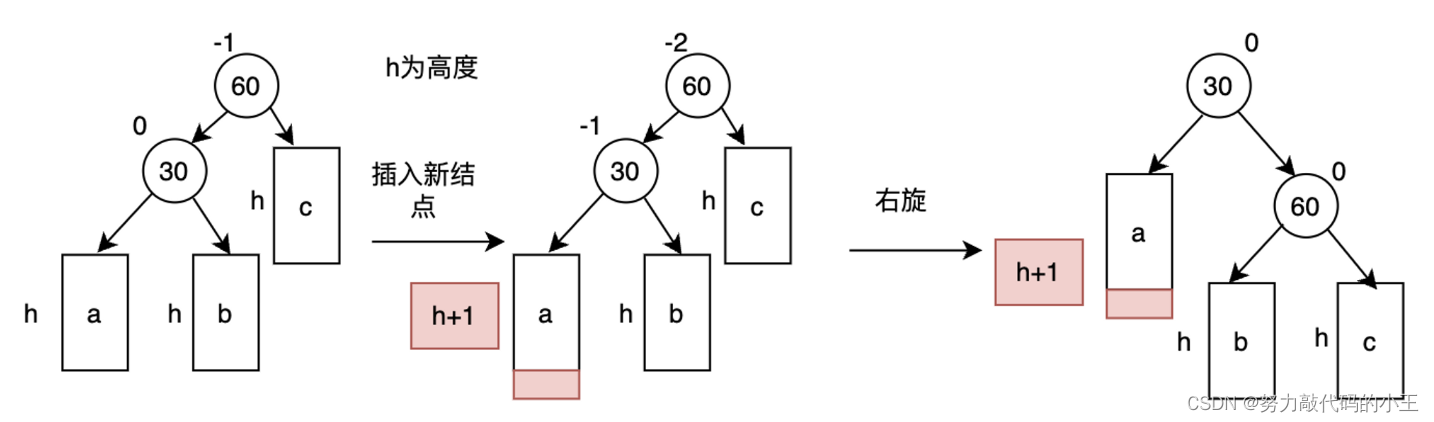
上图在插入前，AVL树是平衡的，新节点插入到30的左子树(注意：此处不是左孩子)中，30左
子树增加了一层，导致以60为根的二叉树不平衡，要让60平衡，只能将60左子树的高度减少一层，右子树增加一层，即将左子树往上提，这样60转下来，因为60比30大，只能将其放在30的右子树，而如果30有右子树，右子树根的值一定大于30，小于60，只能将其放在60的左子树，旋转完成后，更新节点的平衡因子即可。在旋转过程中，有以下几种情况需要考虑：
1. 30节点的右孩子可能存在，也可能不存在
2. 60可能是根节点，也可能是子树
如果是根节点，旋转完成后，要更新根节点
如果是子树，可能是某个节点的左子树，也可能是右子树

//右旋和左旋是一样的
    void RotateR(Node* parent)
    {
        Node* subL=parent->left;
        Node* subLR=subL->right;
        Node* pparent=parent->parent;
        parent->left=subLR;
        subL->right=parent;
        if(subLR!= nullptr)
        {
            subLR->parent=parent;
        }
        parent->parent=subL;
        subL->parent=pparent;
        if(pparent== nullptr)
        {
            _root=subL;
        }
        else if(pparent!= nullptr)
        {
            if(pparent->left==parent)
            {
                pparent->left=subL;
            }
            else if(pparent->right==parent)
            {
                pparent->right=subL;
            }
        }
        parent->_bf=subL->_bf=0;
    }

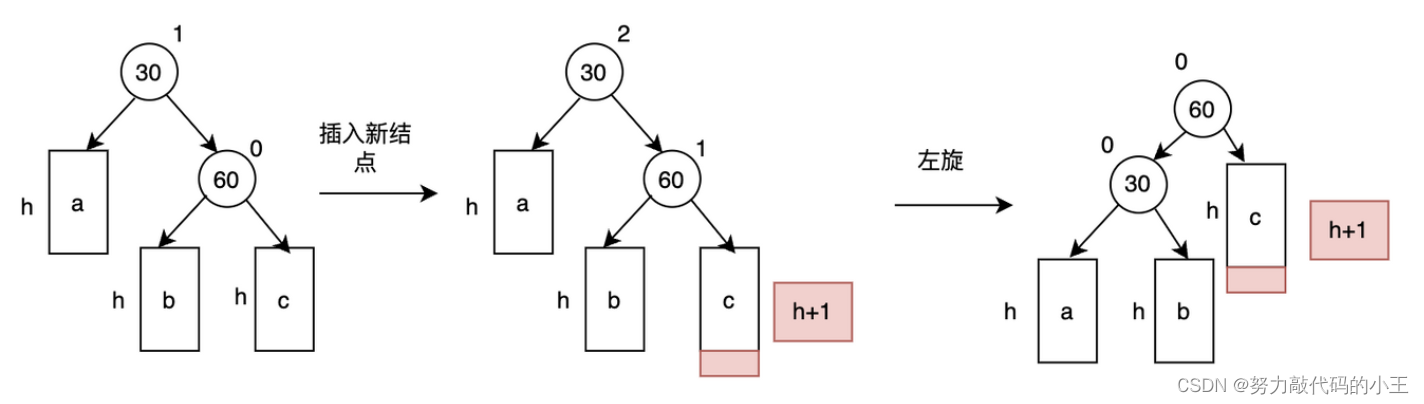
• 新节点插入较高右子树的右侧—右右：左单旋

void RotateL(Node* parent)
    {
        Node* subR=parent->right;
        //右子树的左子树
        Node* subRL=subR->left;
        //旋转的这棵树有可能是子树，所以需要保存parent的parent
        Node* pparent=parent->parent;
        parent->right=subRL;
        subR->left=parent;
        //subLR可能不存在，需要单独判断
        if(subRL!= nullptr)
        {
            subRL->parent = parent;
        }
        parent->parent=subR;
        subR->parent=pparent;
        //如果parent不是子树，就需要把_root给subR
        if(pparent== nullptr)
        {
            _root=subR;
        }
        //如果parent是子树的话，需要改变pparent的指向
        else if(pparent!= nullptr)
        {
            //子树是pparent的左子树/右子树，需要把pparent-left/->right指向subR
            if(pparent->left==parent)
            {
                pparent->left=subR;
            }
            else if(pparent->right==parent)
            {
                pparent->right=subR;
            }
        }
        //更新平衡因子
        subR->_bf=parent->_bf=0;
    }

• 新节点插入较高左子树的右侧—左右：先左单旋再右单旋

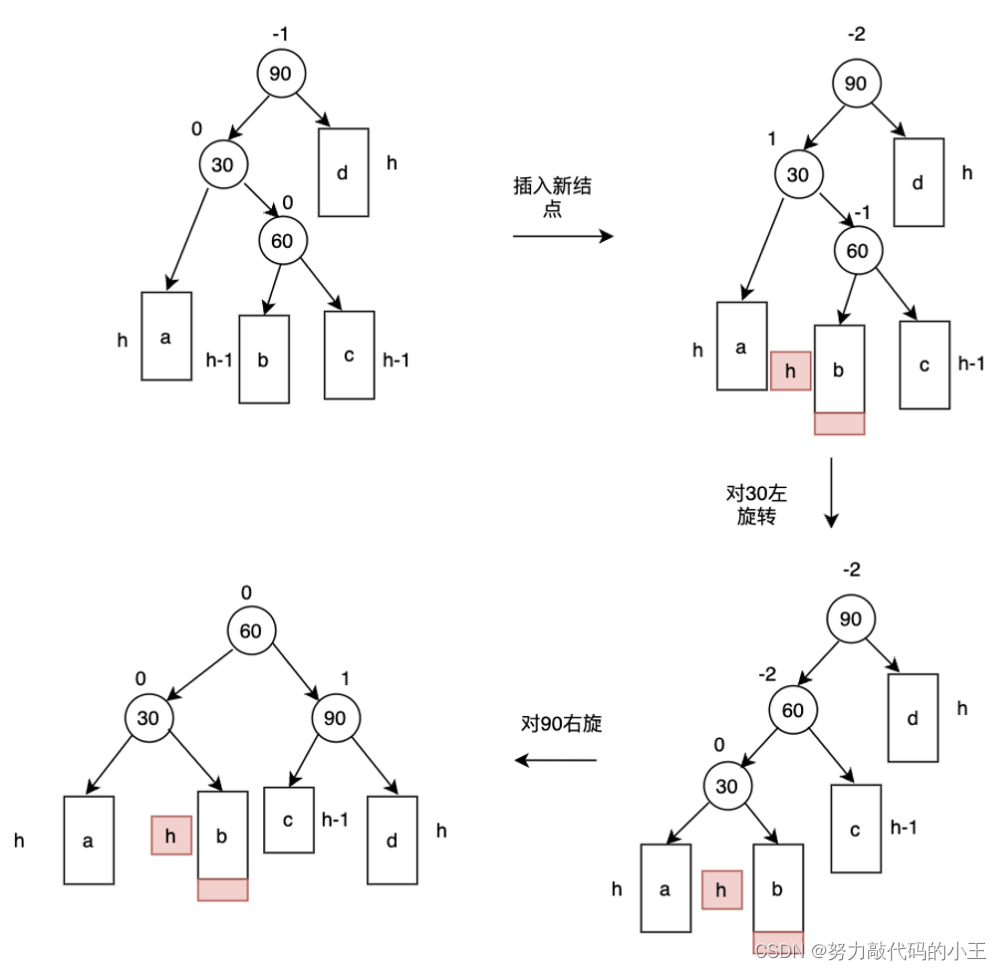
注意：要提前记录60的平衡因子，60这个结点的平衡因子如果是-1，90的平衡因子就会+1，30、60的平衡因子是0，如果平衡因子是1的话，30的平衡因子会-1，60，90的平衡因子是0，但如果平衡因子是0的话，那么30，60，90的平衡因子也是0

void RotateLR(Node* parent)
    {
        Node* subL=parent->left;
        Node* subLR=subL->right;
        int bf=subLR->_bf;
        RotateL(parent->left);
        RotateR(parent);
        if(bf==0)
        {
            subL->_bf=0;
            subLR->_bf=0;
            parent->_bf=0;
        }
        else if(bf==1)
        {
            parent->_bf=0;
            subLR->_bf=0;
            subL->_bf=-1;
        }
        else if(bf==-1)
        {
            parent->_bf=1;
            subLR->_bf=0;
            subL->_bf=0;
        }
        else
        {
            assert(false);
        }

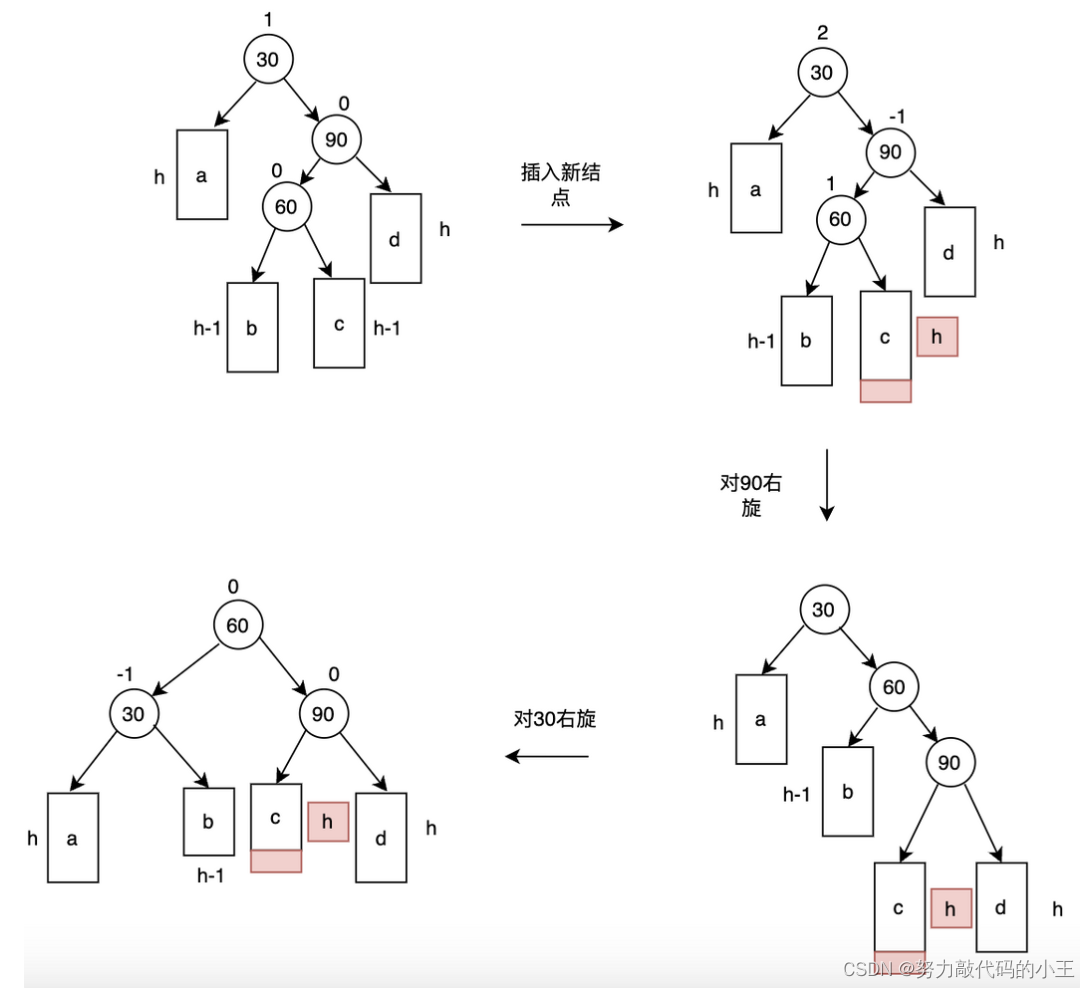
• 新节点插入较高右子树的左侧—右左：先右单旋再左单旋

void RotateRL(Node* parent)
    {
        Node* subR=parent->right;
        Node* subRL=subR->left;
        int bf=subRL->_bf;
        RotateR(parent->right);
        RotateL(parent);
        //可以都更新为0
        if(bf==0)
        {
            subR->_bf=0;
            subRL->_bf=0;
            parent->_bf=0;
        }
        //bf=1,会导致parent少一个右结点
        else if(bf==1)
        {
            subR->_bf=0;
            parent->_bf=-1;
            subRL->_bf=0;
        }
        //bf=-1,会让subR少一个左结点
        else if(bf==-1)
        {
            subR->_bf=0;
            parent->_bf=0;
            subR->_bf=1;
        }
        else
        {
            //出错
            assert(false);
        }
    }