常见的方波信号傅里叶级数展开都是占空比为50%，如方波信号傅里叶级数展开，但有的时候信号的占空比不一定是50%的信号，这时我们要对其进行傅里叶变换或者频谱推导的时候，就不太适用了。因此本文将对占空比任意的方波信号的傅里叶级数展开进行推导。搭配转|周期矩形脉冲信号频谱及特点食用更佳。

傅里叶级数的复数形式

本文推导将使用傅里叶级数变换的复数形式，具体推导可观看B站Dr.CAN的视频纯干货数学推导_傅里叶级数与傅里叶变换_Part4_傅里叶级数的复数形式
这里直接引用结论：周期为T的周期函数f(t)可以展开为$C_n$为系数的一系列级数。

占空比任意方波的傅里叶级数展开

下面我们定义一个周期为T、占空比为D、高电平幅度为A的任意方波信号，其时域波形如下：

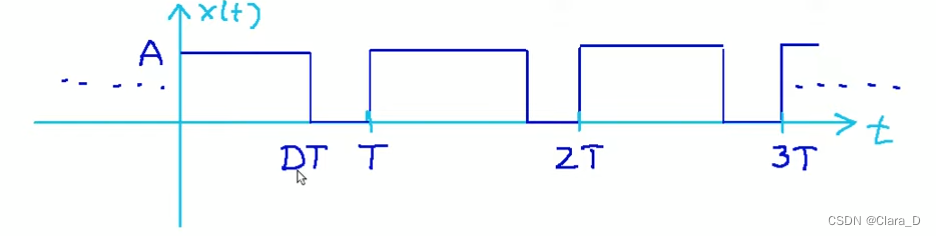
单个周期T内x(t)表达式可写为：
$$\begin{array}{c}x(t)=\{\begin{array}{ll}A& 0\le t<DT\\ 0& DT\le 0<T\end{array}\end{array}$$
下面来计算傅里叶级数的系数：
$$\begin{gathered} C_0=\frac{1}{T}{\int }_0^{DT}x(t)dt=AD \\ {C}_n=\frac{1}{T}{\int }_0^{T}x(t)e^{-jk{\omega }_{0}t}dt=\frac{1}{T}{\int }_0^{DT}A{e}^{-jk{\omega }_{0}t}dt \\ =\frac{A}{T\ast (-jk{\omega }_0)}(e^{-jk{\omega }_{0}DT}-1) \end{gathered}$$
用${\omega }_0=2\pi f_0$代入：
$$\begin{gathered} C_n=\frac{A}{-jk2\pi }(e^{-jk2\pi D}-1)=\frac{A}{jk2\pi }(e^{jk\pi D-e^{-jk\pi D}})e^{-jk\pi D} \\ =\frac{A}{k\pi }sin(k\pi D)e^{-jk\pi D} \end{gathered}$$
因此x(t)的展开式可写为：
$$x(t)=\sum _{-\infty }^{+\infty }\frac{A}{k\pi }sin(k\pi D)e^{jk({\omega }_{0}t-\pi D)}$$
$e^{-jk\pi D}$作为相移因子，如果方波是以t=0奇对称，则没有相移存在。Cn还可以整理为一个sinc函数的形式。