LASSO 回归 的特点是在拟合广义线性模型的同时进行变量筛选(variable selection)和复杂度调整(regularization)。因此不论目标因变量(dependent/response varaible)是连续的(continuous),还是二元或者多元离散的(discrete),都可以用 LASSO 回归建模然后预测。
这里的变量筛选是指不把所有的变量都放入模型中进行拟合,而是有选择的把变量放入模型从而得到更好的性能参数。复杂度调整是指通过一系列参数控制模型的复杂度,从而避免过度拟合(overfitting)。
对于线性模型来说,复杂度与模型的变量数有直接关系,变量数越多,模型复杂度就越高。更多的变量在拟合时往往可以给出一个看似更好的模型,但是同时也面临过度拟合的危险。此时如果用全新的数据去验证模型(validation),通常效果很差。一般来说,变量数大于数据点数量很多,或者某一个离散变量有太多独特值时,都有可能过度拟合。
LASSO 回归复杂度调整的程度由参数 λ来控制,λ越大对变量较多的线性模型的惩罚力度就越大,从而最终获得一个变量较少的模型。 LASSO 回归与 Ridge 回归同属于一个被称为 Elastic Net 的广义线性模型家族。 这一家族的模型除了相同作用的参数 λ之外,还有另一个参数 α来控制应对高相关性(highly correlated)数据时模型的性状。 LASSO 回归 α=1,Ridge 回归 α=0 ,一般 Elastic Net 模型 0<α<1。
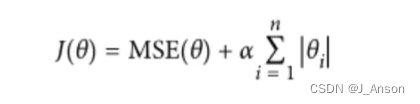
Lasso回归和岭回归的同和异:
Lasso回归对比岭回归,公式上只有theta项的区别,Lasso回归的theta项是加了绝对值。
相同:都可以用来解决标准线性回归的过拟合问题。
不同:
1)lasso 可以用来做 feature selection,而 ridge 不行。或者说,lasso 更容易使得权重变为 0,而 ridge 更容易使得权重接近 0。
2)从贝叶斯角度看,lasso(L1 正则)等价于参数 w 的先验概率分布满足拉普拉斯分布,而 ridge(L2 正则)等价于参数 w 的先验概率分布满足高斯分布。
加入 L1 或 L2 正则化,让权值尽可能小,最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。
可以设想一下对于一个线性回归方程,若参数很大,那么只要数据偏移一点点,就会对结果造成很大的影响;但如果参数足够小,数据偏移得多一点也不会对结果造成什幺影响,一种流行的说法是『抗扰动能力强』。
过拟合问题解决方法:
(1)丢弃一些对我们最终预测结果影响不大的特征,具体哪些特征需要丢弃可以通过PCA算法来实现;
(2)使用正则化技术,保留所有特征,但是减少特征前面的参数的大小,具体就是修改线性回归中的损失函数形式即可,岭回归以及Lasso回归就是这么做的。
从数学上来说,它由一个带有附加正则化项的线性模型组成。最小化的目标函数是:
(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1下面,我们通过对比实验来观察不同的alpha值对每一个产生的theta结果的影响。
一、导包
from sklearn.linear_model import Lasso
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
二、生成基础数据
np.random.seed(50)
m = 40
X = 3 * np.random.rand(m, 1)
y = 0.5 * X + np.random.rand(m, 1) / 1.5 + 1三、查看数据落图情况
plt.plot(X, y, "b.")
plt.xlabel("X")
plt.ylabel("y")
plt.axis([0, 3, 0, 3])
plt.show()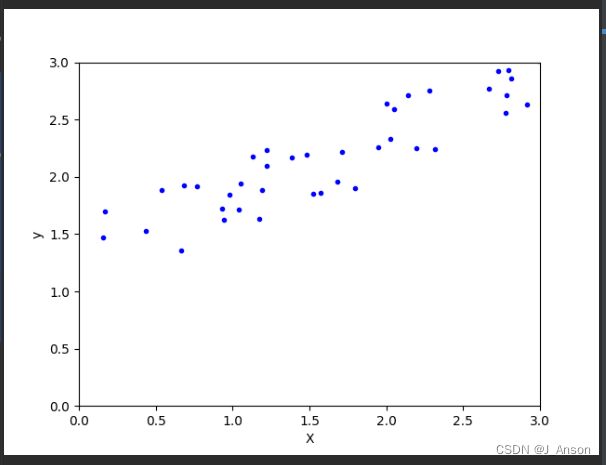
四、利用Lasso回归模型,建立对比实验
def plot_model(model_class, data_X, polynomial, alphas, **model_kargs):
for alpha, style in zip(alphas, ("b-", "g--", "r:")):
model = model_class(alpha, **model_kargs)
if polynomial:
model = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("StandardScaler", StandardScaler()),
("lin_reg", model)])
model.fit(X, y)
y_new_regul = model.predict(data_X)
lw = 2 if alpha > 0 else 1
plt.plot(data_X, y_new_regul, style, linewidth=lw, label=f"alpha={alpha}")
plt.plot(X, y, "b.", linewidth=3)
plt.legend()五、准备需拟合的数据,并拟合画图
X_new = np.linspace(0, 3, 100).reshape(100, 1)
plt.figure(figsize=(14, 6))
plt.subplot(121)
plot_model(Lasso, data_X=X_new, polynomial=False, alphas=(0, 0.01, 0.1))
plt.subplot(122)
plot_model(Lasso, data_X=X_new, polynomial=True, alphas=(0, 0.01, 0.1))
plt.show()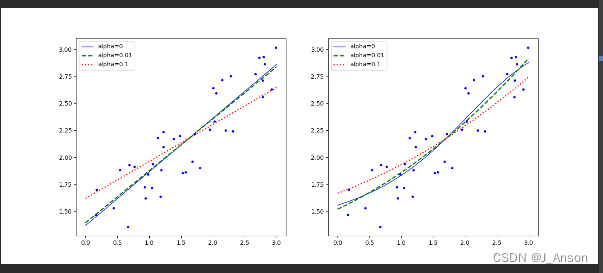
代码在运行过程中,针对alpha=0的情况,会发出警告,拟合不收敛。
对比不同的alpha值的运行结果,可以发现alpha值越大,拟合的结果趋向平稳,效果越好。