传统的集合运算
在数据库中的关系代数运算有以下三种基本运算
- 并
- 交
- 差
必须满足两个表之间的属性个数必须一样。(必须具有相容性)
投影与选择运算
- 投影:π
L
_L
L( R )
解释->π是投影符号,L是R表中的属性列,从R中选出L的属性列,叫做投影
好比SQL语句:select sno from student,从学生表中投影出sno学号。(当然投影属性可以不止一个,用逗号隔开就好,不管是SQL语句还是关系投影都是用逗号隔开就行) - 选择:σ
X
_X
X
θ
_θ
θ
Y
_Y
Y(R)
解释->条件选择, X _X X θ _θ θ Y _Y Y表示条件θ在这里代表比较运算符大于或等于这些,满足条件的就从R表中选择出来,就叫做选择操作
好比SQL语句:select * from student where sno=‘01’,这里没有作投影操作,所以只要满足条件就会整个元输出,所以是 * 。 - Tips
这里的投影与选择操作都是基于集合来运算的,所以可以结合并交叉运算符来写出更为复杂的查询语句。
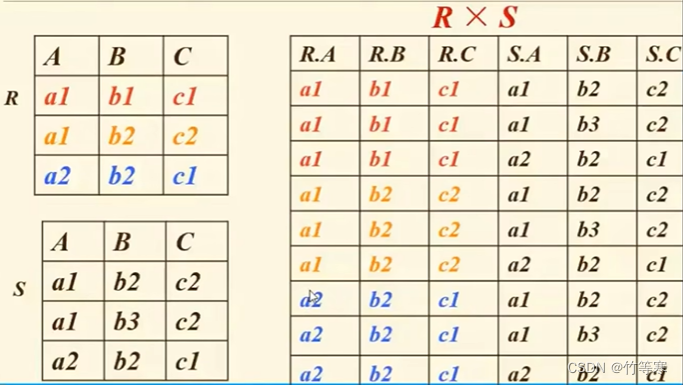
连接运算
-
R × X _X X θ _θ θ Y _Y Y S
其实就是将两个表的元组拼在一起作笛卡尔积运算,并且这是带有条件的运算, X _X X θ _θ θ Y _Y Y就代表连接条件
-
R ∞ S (自然连接)
没有写连接条件的就叫做自然连接,自然连接就是等值连接 X _X X = _= = Y _Y Y,但是他会将两个表的相同属性列合并。如果是显示的写出该等值条件,也就是上述的等值连接就不会将相同属性列去掉,而是属于上述R ∞ X _X X θ _θ θ Y _Y Y S 操作。这也是自然连接的一个好处,能自动将相同属性列去掉只保留一份。
注意:自然连接两个表的属性列的属性名字要相同才能进行自然连接。既然要同名,那我可以使用ρ 直接给他换个名字之后再进行自然连接(就是下面提到的重命名)
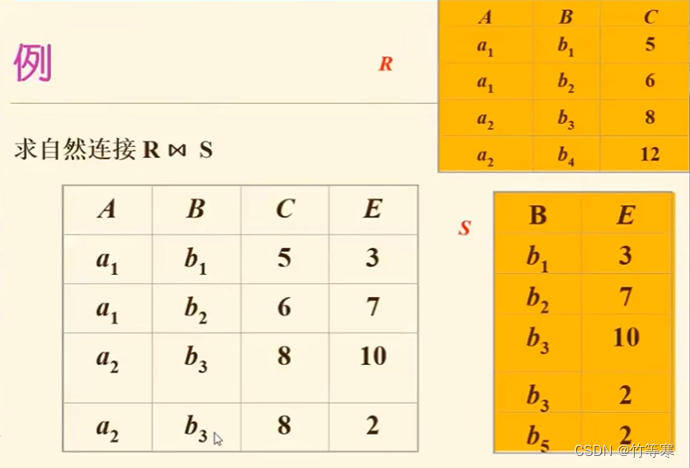
自然连接默认做的操作- R×S做笛卡尔积操作
- 将属性相等的进行等值条件连接
- 去除重复的属性
-
选择投影的等值条件连接与自然连接是等价的。
R▷◁S=∏B(σR.A=S.A (R×S))
除法
象集
这个概念这是如其名了,十分抽象。不过老师的PPT的一个例子讲的很好。

如果但看概念真的很抽象,还是例子一看就懂。
意思就是假如你要找小明的象集,那在这个关系表,有关小明的元组中将小明这个属性值去除掉,每一个元组除了小明这个属性值外就对应一个象集元素,全部加起来就是小明的象集。
有点像现实生活中的关系,你跟哪个群体是一伙的,那么那个团体的人就是你的人际关系的一个元素,你的所有群体的每一个团体集合就是一个象集。
除法
象集理解了除法就好理解了,两个表做除法就是一个被除数与除数的关系。
- 被除数与除数
在数据库的关系代数中,作为被除数一方,是提供给除数去对比的,让除数找到自己的部分,然后找到与自己部分或者自己就在那个集合里面组成的那个元组的其他属性,然后那个就是俩表做除法的结果。
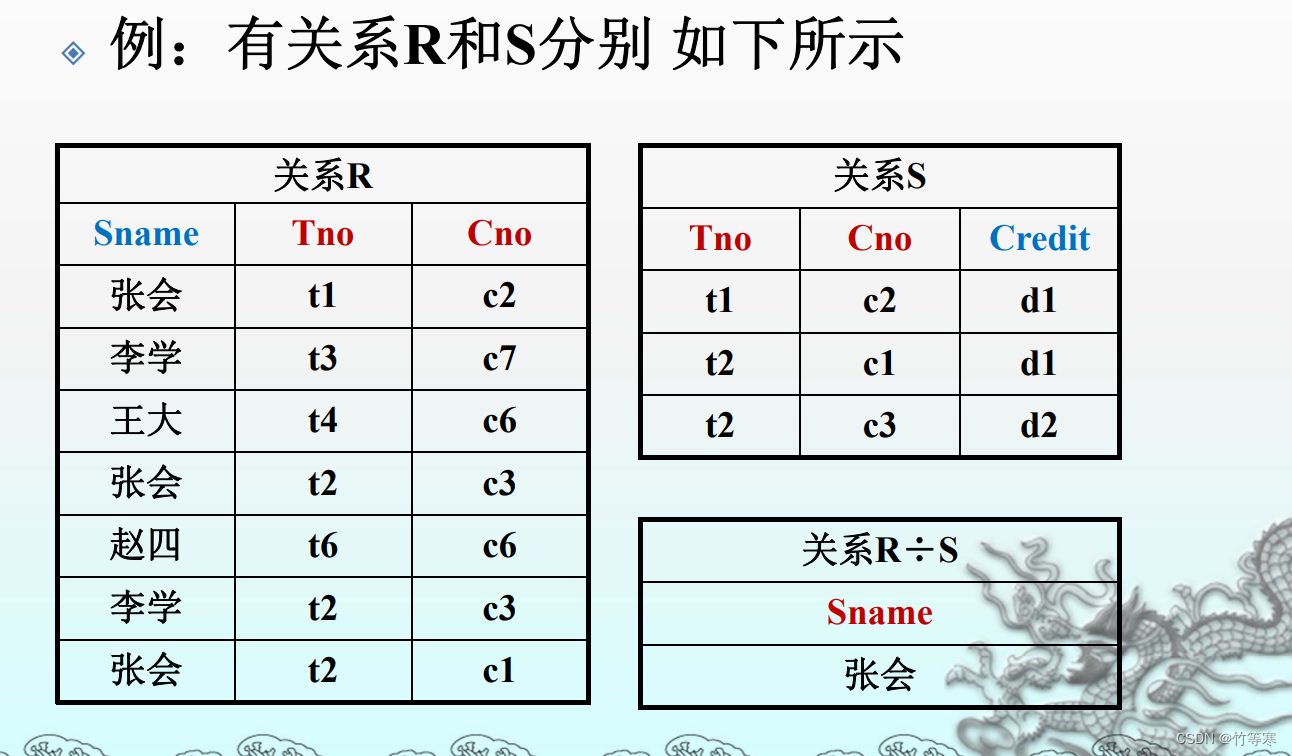
用文字解释就很是挺抽象的,老师的PPT例子也做得很好,下面给出截图。 - 总的来说就是
被除数就是参照表,除数去找到自己的一部分,在被除数中奖自己的一部分删除掉,剩下的属性数据就是除法的结果。
收获
在集合中做运算一律都是不会出现重复的,因为集合本身就是这样定义的,没有重复的元素。
重命名
- ρ
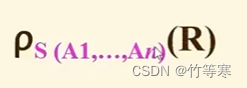
将R重命名为S,如果不写括号内的A1A2…就代表原封不动的将R的属性名搬过来给S,只是将R重名为S而已,如果要改变属性列就要写括号内的内容。