tensorflow和pytorch很多都是相似的，这里以pytorch为例。

一、L1范数损失 L1Loss

L1范数损失（L1 norm loss）是一种常用的损失函数，用于衡量模型预测值与真实值之间的差异。它是基于L1范数（也称为曼哈顿距离）的衡量方式。L1范数是指向量中各个元素绝对值之和。

在机器学习和深度学习中，L1范数损失通常用于正则化和稀疏性推动。通过最小化L1范数损失，可以鼓励模型产生稀疏的权重或特征选择，因为L1范数倾向于将一些权重或特征设置为零。

L1范数损失的定义如下：

L1范数损失 = ∑|y - ŷ|

其中，y表示真实值，ŷ表示模型的预测值，|x|表示x的绝对值，∑表示求和运算。

在训练过程中，通过最小化L1范数损失来调整模型的参数，使模型能够更好地拟合训练数据，并尽可能减少预测值与真实值之间的差异。

计算 output 和 target 之差的绝对值。

torch.nn.L1Loss(reduction='mean')

参数：

reduction-三个值，none: 不使用约简；mean:返回loss和的平均值；sum:返回loss的和。默认：mean。

二、均方误差损失 MSELoss

均方误差损失（Mean Squared Error Loss），通常简称为MSE损失，是深度学习中常用的一种损失函数，用于衡量模型预测值与真实值之间的差异。

MSE损失计算方式如下：
MSE损失 = 1/n * ∑(y - ŷ)^2

其中，y表示真实值，ŷ表示模型的预测值，n表示样本数量，∑表示求和运算。

MSE损失首先计算预测值与真实值之间的差异，然后将差值平方，再对所有样本进行求和，最后除以样本数量，得到平均值。因此，MSE损失是预测值与真实值差异的平方的平均值。

MSE损失的优点是对较大的预测误差有较高的惩罚，因为差异的平方放大了较大的误差。同时，MSE损失在数学性质上也比较好，易于计算和求导。

在训练过程中，通过最小化MSE损失来调整模型的参数，使模型能够更好地拟合训练数据，并尽可能减少预测值与真实值之间的差异。

计算 output 和 target 之差的均方差。

torch.nn.MSELoss(reduction='mean')

参数：

reduction-三个值，none: 不使用约简；mean:返回loss和的平均值；sum:返回loss的和。默认：mean。

三、交叉熵损失 CrossEntropyLoss

当训练有 C 个类别的分类问题时很有效. 可选参数 weight 必须是一个1维 Tensor, 权重将被分配给各个类别. 对于不平衡的训练集非常有效。

在多分类任务中，经常采用 softmax 激活函数+交叉熵损失函数，因为交叉熵描述了两个概率分布的差异，然而神经网络输出的是向量，并不是概率分布的形式。所以需要 softmax激活函数将一个向量进行“归一化”成概率分布的形式，再采用交叉熵损失函数计算 loss。

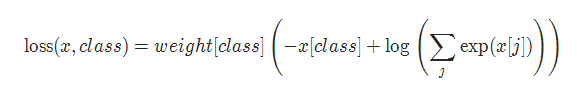
交叉熵损失（CrossEntropyLoss）是深度学习中常用的一种损失函数，尤其适用于分类问题。它衡量模型的预测概率分布与真实标签之间的差异。

交叉熵损失的计算方式依赖于模型的输出形式。通常，在分类问题中，模型会输出一个概率分布，表示每个类别的预测概率。而真实标签通常以one-hot编码的形式表示。

交叉熵损失的计算方式如下：
CrossEntropyLoss = -∑(y * log(ŷ))

其中，y表示真实标签的概率分布（one-hot编码），ŷ表示模型的预测概率分布，∑表示求和运算。

交叉熵损失首先将真实标签的概率分布与模型的预测概率分布进行逐元素相乘，然后取对数，最后对所有元素求和并取相反数。通过取相反数，损失值越小表示模型的预测越准确。

交叉熵损失的优点是能够有效地激励模型输出的概率分布接近真实标签的分布。它在训练过程中可以推动模型更快地收敛，并在分类任务中产生更好的结果。

在训练过程中，通过最小化交叉熵损失来调整模型的参数，使模型能够更好地拟合训练数据，并提高分类准确性。

torch.nn.CrossEntropyLoss(weight=None,ignore_index=-100, reduction='mean')

参数：

weight (Tensor, optional) – 自定义的每个类别的权重. 必须是一个长度为 C 的 Tensor；

ignore_index (int, optional) – 设置一个目标值, 该目标值会被忽略, 从而不会影响到输入的梯度。

reduction-三个值，none: 不使用约简；mean:返回loss和的平均值；sum:返回loss的和。默认：mean。

四、KL 散度损失 KLDivLoss

KL散度损失（KLDivLoss），也称为Kullback-Leibler散度损失，是深度学习中常用的一种损失函数，用于衡量两个概率分布之间的差异。

KL散度是一种度量两个概率分布之间差异的指标。KL散度损失用于衡量模型的预测概率分布与真实概率分布之间的差异。通常情况下，真实概率分布由one-hot编码表示，而模型的预测概率分布则由模型输出的概率向量表示。

KL散度损失的计算方式如下：
KLDivLoss = ∑(y * log(y / ŷ))

其中，y表示真实概率分布（one-hot编码），ŷ表示模型的预测概率分布，∑表示求和运算。

KL散度损失首先计算真实概率分布与模型的预测概率分布的比值，然后取对数，最后将两者逐元素相乘并求和。KL散度损失值越小表示模型的预测分布与真实分布越接近。

KL散度损失在训练过程中鼓励模型生成与真实分布相似的输出，并促使模型更好地拟合训练数据。在训练分类模型时，使用KL散度损失可以提高模型的分类准确性。

需要注意的是，KL散度损失不具有对称性，即KLDivLoss(P, Q)与KLDivLoss(Q, P)的值可能不相等。因此，在实际应用中，我们通常将KL散度损失与交叉熵损失（CrossEntropyLoss）结合使用，以获得更好的效果。

计算 input 和 target 之间的 KL 散度。KL 散度可用于衡量不同的连续分布之间的距离, 在连续的输出分布的空间上(离散采样)上进行直接回归时 很有效。

torch.nn.KLDivLoss(reduction='mean')

参数：

reduction-三个值，none: 不使用约简；mean:返回loss和的平均值；sum:返回loss的和。默认：mean。

五、二进制交叉熵损失 BCELoss

二进制交叉熵损失（Binary Cross-Entropy Loss），通常简称为BCE损失，是深度学习中用于二分类问题的一种常见损失函数。它用于衡量模型的二分类输出与真实标签之间的差异。

BCE损失的计算方式如下：
BCE损失 = -[y * log(ŷ) + (1 - y) * log(1 - ŷ)]

其中，y表示真实标签（取值为0或1），ŷ表示模型的预测概率（取值在0到1之间）。

BCE损失根据真实标签的取值分别计算两个部分的损失，分别对应真实标签为1和0的情况。当真实标签为1时，损失函数只考虑模型预测为1的部分，即-y * log(ŷ)；当真实标签为0时，损失函数只考虑模型预测为0的部分，即-(1 - y) * log(1 - ŷ)。

BCE损失函数的优点是在二分类问题中比较直观且易于计算。它对于模型预测接近真实标签的情况有较低的损失，同时对于模型预测明显错误的情况有较高的惩罚。

在训练过程中，通过最小化BCE损失来调整模型的参数，使模型能够更好地拟合训练数据，并提高二分类任务的准确性。

二分类任务时的交叉熵计算函数。用于测量重构的误差, 例如自动编码机. 注意目标的值 t[i] 的范围为0到1之间。

torch.nn.BCELoss(weight=None, reduction='mean')

参数：

weight (Tensor, optional) – 自定义的每个 batch 元素的 loss 的权重. 必须是一个长度为 “nbatch” 的 的 Tensor

六、BCEWithLogitsLoss

BCEWithLogitsLoss（Binary Cross-Entropy With Logits Loss）是深度学习中常用的一种损失函数，通常用于二分类问题，特别是当模型的输出不经过激活函数（如sigmoid函数）时。

BCEWithLogitsLoss结合了sigmoid激活函数和二进制交叉熵损失，以提高数值稳定性和计算效率。该损失函数接受模型的原始输出，即未经过激活函数的logits（通常是线性层的输出），并在内部应用sigmoid函数来计算预测概率。

BCEWithLogitsLoss的计算方式如下：
BCEWithLogitsLoss = -[y * log(σ(ŷ)) + (1 - y) * log(1 - σ(ŷ))]

其中，y表示真实标签（取值为0或1），ŷ表示模型的输出logits，σ表示sigmoid函数。

与BCELoss不同的是，BCEWithLogitsLoss直接在内部应用sigmoid函数，省去了手动应用sigmoid函数的步骤。通过将sigmoid函数的输出与真实标签进行比较，BCEWithLogitsLoss计算了正类和负类的损失。

BCEWithLogitsLoss的优点是对于模型输出在较大范围内的数值具有数值稳定性，避免了数值上溢或下溢的问题。此外，由于内部应用了sigmoid函数，BCEWithLogitsLoss在数学上也比较好处理和求导。

在训练过程中，通过最小化BCEWithLogitsLoss来调整模型的参数，使模型能够更好地拟合训练数据，并提高二分类任务的准确性。

BCEWithLogitsLoss损失函数把 Sigmoid 层集成到了 BCELoss 类中. 该版比用一个简单的 Sigmoid 层和 BCELoss 在数值上更稳定, 因为把这两个操作合并为一个层之后, 可以利用 log-sum-exp 的 技巧来实现数值稳定。

torch.nn.BCEWithLogitsLoss(weight=None, reduction='mean', pos_weight=None)

参数：

weight (Tensor, optional) – 自定义的每个 batch 元素的 loss 的权重. 必须是一个长度 为 “nbatch” 的 Tensor

七、MarginRankingLoss

MarginRankingLoss（边际排序损失）是一种用于学习排序模型的损失函数，常用于训练具有排序目标的模型，例如排序任务、排序推荐系统等。

MarginRankingLoss的目标是将正样本的预测得分（正例）与负样本的预测得分（负例）之间的差异最大化，同时保持一定的边际（margin）。这样可以促使模型在预测时更好地区分正负样本，从而提高排序性能。

MarginRankingLoss的计算方式如下：
MarginRankingLoss = max(0, -y * (ŷ_p - ŷ_n) + margin)

其中，y为标签，取值为1或-1，表示正样本或负样本；ŷ_p为正样本的预测得分；ŷ_n为负样本的预测得分；margin为边际，是一个预先指定的超参数。

MarginRankingLoss首先计算正样本的预测得分与负样本的预测得分之差，然后将其与边际进行比较。如果差异大于边际，则损失为0，表示模型已经达到了边际的要求。如果差异小于边际，则损失为差异的负值，以惩罚模型对正负样本的错误排序。

通过最小化MarginRankingLoss来调整模型的参数，可以使模型更好地区分正负样本，从而提高排序任务的性能。适当选择边际参数可以根据具体任务的需求来平衡模型对正负样本的排序关系。

torch.nn.MarginRankingLoss(margin=0.0, reduction='mean')

对于 mini-batch(小批量) 中每个实例的损失函数如下：

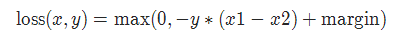
参数：margin:默认值0

八、HingeEmbeddingLoss

HingeEmbeddingLoss（铰链嵌入损失）是一种用于训练支持向量机（Support Vector Machine，SVM）模型的损失函数，常用于二分类任务。它的目标是鼓励模型将正负样本分开，并在一定程度上惩罚分类错误。

HingeEmbeddingLoss的计算方式如下：
HingeEmbeddingLoss = max(0, margin - y * ŷ)

其中，y为标签，取值为1或-1，表示正样本或负样本；ŷ为模型的预测得分；margin为边际，是一个预先指定的超参数。

HingeEmbeddingLoss首先计算预测得分与标签的乘积，如果结果大于边际，则损失为0，表示模型已经达到了边际的要求。如果结果小于边际，则损失为差异的负值，以惩罚模型对正负样本的错误分类。

HingeEmbeddingLoss的特点是对于预测得分与标签之间的差异有一个较大的惩罚，这使得模型在训练过程中更加关注那些预测得分与标签之间差异较大的样本。这有助于将正负样本分开，并增强模型的分类能力。

通过最小化HingeEmbeddingLoss来调整模型的参数，可以使模型更好地分类正负样本，从而提高二分类任务的性能。适当选择边际参数可以根据具体任务的需求来平衡模型对正负样本分类的要求。

torch.nn.HingeEmbeddingLoss(margin=1.0,  reduction='mean')

对于 mini-batch(小批量) 中每个实例的损失函数如下：

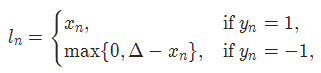
参数：margin:默认值1

九、多标签分类损失 MultiLabelMarginLoss

MultiLabelMarginLoss（多标签边际损失）是一种用于多标签分类任务的损失函数。它适用于同时处理多个标签，并鼓励模型在每个标签上的预测与真实标签之间有较大的差异。

MultiLabelMarginLoss的计算方式如下：
MultiLabelMarginLoss = max(0, margin - y * ŷ_i + (1 - y) * ŷ_j)

其中，y是一个二进制矩阵，表示真实标签，每行对应一个样本的标签，ŷ是一个浮点数矩阵，表示模型的预测输出，每行对应一个样本的预测概率，margin是边际参数。

MultiLabelMarginLoss对于每个样本和每个标签都计算了一个边际损失。对于每个样本，该损失函数选择预测得分与真实标签之间的差异最大的两个标签，并计算它们之间的边际损失。如果两个标签之间的差异小于边际，则损失为0，表示模型已经达到了边际的要求。如果差异大于边际，则损失为差异的负值，以惩罚模型对标签的错误排序。

MultiLabelMarginLoss的优点是能够处理多标签分类任务，并对模型在每个标签上的预测进行差异化的训练。它帮助模型在每个标签上进行更准确的分类，从而提高多标签分类任务的性能。

通过最小化MultiLabelMarginLoss来调整模型的参数，可以使模型更好地分类多个标签，并提高多标签分类任务的准确性。合理选择边际参数可以平衡模型对标签差异的要求。

torch.nn.MultiLabelMarginLoss(reduction='mean')

对于mini-batch(小批量) 中的每个样本按如下公式计算损失：

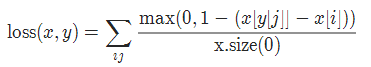
十、平滑版L1损失 SmoothL1Loss

平滑版L1损失（SmoothL1Loss），也称为Huber损失，是一种用于回归任务的损失函数。它在L1损失和L2损失之间提供了一种平滑的过渡，可以减少异常值对损失函数的敏感性。

SmoothL1Loss的计算方式如下：
SmoothL1Loss =

0.5 * (y - ŷ)^2，如果 |y - ŷ| < 1
|y - ŷ| - 0.5，否则
其中，y表示真实值，ŷ表示模型的预测值。

SmoothL1Loss在|y - ŷ|小于1时采用平方差损失，否则采用L1损失。这样，在真实值和预测值之间存在一个平滑的过渡区域，使损失函数对异常值的响应相对较小。

平滑版L1损失相对于L2损失（平方差损失）具有以下特点：

1. 平滑度：相比于L2损失，SmoothL1Loss在接近真实值时具有更好的平滑性，对离群值的响应相对较小。
2. 鲁棒性：由于平滑过渡区域，SmoothL1Loss对于异常值的影响较小，使得模型更具鲁棒性。
3. 渐进性：在预测值与真实值之间的差异较小时，SmoothL1Loss接近平方差损失，有利于模型学习小的差异。

通过最小化SmoothL1Loss来调整模型的参数，可以使模型在回归任务中更好地拟合数据，同时减少对异常值的敏感性。

torch.nn.SmoothL1Loss(reduction='mean')

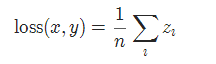
其中：

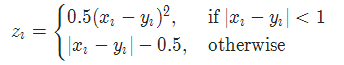
十一、2分类的logistic损失 SoftMarginLoss

对于二分类问题，SoftMarginLoss（也称为Logistic Loss或Logistic Regression Loss）是一种常用的损失函数，用于衡量模型输出与真实标签之间的差异。

SoftMarginLoss的计算方式如下：
SoftMarginLoss = log(1 + exp(-y * ŷ))

其中，y表示真实标签（取值为1或-1），ŷ表示模型的预测输出。

SoftMarginLoss基于逻辑斯蒂回归（Logistic Regression）的概念，它使用了Sigmoid函数将预测输出映射到0到1之间的概率值，以表示样本属于正类的可能性。

SoftMarginLoss的优点是在计算损失时，将模型输出通过Sigmoid函数转换为概率值，并将其与真实标签进行比较。当模型对正样本的预测概率较低或对负样本的预测概率较高时，SoftMarginLoss会给予较高的损失，促使模型更好地拟合数据。

在训练过程中，通过最小化SoftMarginLoss来调整模型的参数，可以使模型在二分类任务中更好地学习样本的类别边界，并提高分类准确性。SoftMarginLoss在逻辑斯蒂回归和二分类问题中得到了广泛应用。

torch.nn.SoftMarginLoss(reduction='mean')

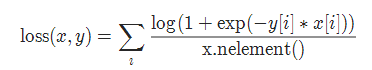
十二、多标签 one-versus-all 损失 MultiLabelSoftMarginLoss

多标签One-Versus-All损失（MultiLabelSoftMarginLoss）是一种用于多标签分类任务的损失函数。它基于逻辑斯蒂回归（Logistic Regression）的概念，适用于训练能够处理多个标签的模型。

MultiLabelSoftMarginLoss的计算方式如下：
MultiLabelSoftMarginLoss = -∑[y_i * log(σ(ŷ_i)) + (1 - y_i) * log(1 - σ(ŷ_i))]

其中，y_i是一个二进制矩阵，表示真实标签，每行对应一个样本的标签，ŷ_i是一个浮点数矩阵，表示模型的预测输出，每行对应一个样本的预测概率，σ表示Sigmoid函数。

MultiLabelSoftMarginLoss计算每个标签的二分类损失，并将它们相加得到总体损失。对于每个标签，该损失函数将模型的预测概率通过Sigmoid函数转换为0到1之间的概率值，并与真实标签进行比较。当模型对正样本的预测概率较低或对负样本的预测概率较高时，MultiLabelSoftMarginLoss会给予较高的损失，促使模型更好地拟合数据。

MultiLabelSoftMarginLoss的优点是能够处理多标签分类任务，并对模型在每个标签上的预测进行差异化的训练。它鼓励模型在每个标签上学习独立的二分类决策边界，从而提高多标签分类任务的性能。

通过最小化MultiLabelSoftMarginLoss来调整模型的参数，可以使模型更好地分类多个标签，并提高多标签分类任务的准确性。该损失函数在多标签分类和逻辑斯蒂回归中得到了广泛应用。

torch.nn.MultiLabelSoftMarginLoss(weight=None, reduction='mean')

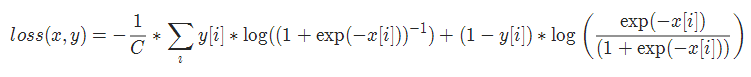
十三、cosine 损失 CosineEmbeddingLoss

CosineEmbeddingLoss（余弦嵌入损失）是一种用于学习嵌入空间中向量之间的相似性的损失函数。它常用于度量两个向量之间的余弦相似性，并鼓励相似的向量之间的余弦相似性接近1，不相似的向量之间的余弦相似性接近-1。

CosineEmbeddingLoss的计算方式如下：
CosineEmbeddingLoss =

• cos(θ)，如果 y = 1
• max(0, cos(θ) - margin)，如果 y = -1

其中，θ表示两个向量之间的夹角，cos(θ)表示它们的余弦相似性，y表示标签（取值为1或-1），margin是边际参数。

当标签y为1时，CosineEmbeddingLoss仅计算两个向量之间的余弦相似性的负值，即1减去cos(θ)。这鼓励相似的向量之间的余弦相似性接近1。

当标签y为-1时，CosineEmbeddingLoss计算余弦相似性与边际之间的差异，并保证损失为非负值。这鼓励不相似的向量之间的余弦相似性接近-1，并且相似度超过边际。

CosineEmbeddingLoss的优点是能够在嵌入空间中度量向量之间的相似性，并通过调整边际参数来控制相似性的要求。它常用于度量文本、图像等领域中的向量相似性，如文本相似度、图像检索等任务。

通过最小化CosineEmbeddingLoss来调整模型的参数，可以使模型学习到合适的向量表示，从而提高向量之间的相似性度量任务的性能。

torch.nn.CosineEmbeddingLoss(margin=0.0, reduction='mean')

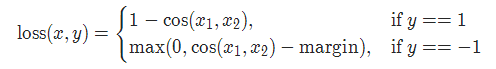
参数：

margin:默认值0

十四、多类别分类的hinge损失 MultiMarginLoss

多类别分类的Hinge损失（MultiMarginLoss）是一种常用的损失函数，适用于多类别分类任务。它鼓励模型将正确类别的得分与错误类别的得分之间的差异最大化。

MultiMarginLoss的计算方式如下：
MultiMarginLoss = ∑[max(0, margin - y + ŷ_i)]

其中，y表示真实类别的索引（从0到类别数减1），ŷ_i表示模型对类别i的预测得分，margin是边际参数。

MultiMarginLoss对于每个样本，计算了真实类别与其他类别之间的差异，并通过边际参数来控制差异的要求。如果真实类别的得分与错误类别的得分之差大于边际，损失为0，表示模型已经达到了边际的要求。如果差异小于边际，则损失为差异的负值。

MultiMarginLoss的优点是能够在多类别分类任务中推动模型将正确类别的得分提高，同时将错误类别的得分降低。它对于分类决策边界的学习非常有用，并可以在训练过程中增强模型的分类能力。

通过最小化MultiMarginLoss来调整模型的参数，可以使模型在多类别分类任务中更好地学习类别之间的差异，并提高分类准确性。边际参数的选择可以根据具体任务的需求来平衡模型对正确类别和错误类别的差异要求。

torch.nn.MultiMarginLoss(p=1, margin=1.0, weight=None,  reduction='mean')

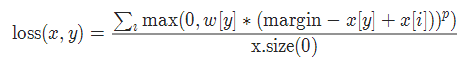
参数：

p=1或者2 默认值：1

margin:默认值1

十五、三元组损失 TripletMarginLoss

三元组损失（TripletMarginLoss）是一种用于训练嵌入模型的损失函数，用于学习具有良好特征表示的嵌入空间。它鼓励使同一类别的样本在嵌入空间中更接近，而不同类别的样本在嵌入空间中更远离。

TripletMarginLoss的计算方式如下：
TripletMarginLoss = max(d(a, p) - d(a, n) + margin, 0)

其中，d(a, p)表示锚样本a与正样本p之间的距离，d(a, n)表示锚样本a与负样本n之间的距离，margin是边际参数。

TripletMarginLoss对于每个锚样本，计算其与正样本之间的距离与其与负样本之间的距离之差，并与边际进行比较。如果差异大于边际，则损失为0，表示模型已经达到了边际的要求。如果差异小于边际，则损失为差异与边际之间的正值。

TripletMarginLoss的目标是通过调整嵌入模型的参数，使同一类别的样本在嵌入空间中更加接近，而不同类别的样本在嵌入空间中更远离。这有助于学习到具有良好区分度的特征表示，适用于许多任务，如人脸识别、图像检索等。

通过最小化TripletMarginLoss来调整模型的参数，可以使模型在训练过程中学习到更好的嵌入表示，从而提高相关任务的性能。选择合适的边际参数可以平衡模型对样本之间距离的要求。

和孪生网络相似，具体例子：给一个A，然后再给B、C，看看B、C谁和A更像。

torch.nn.TripletMarginLoss(margin=1.0, p=2.0, eps=1e-06, swap=False, reduction='mean')

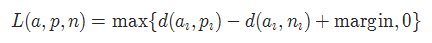
其中：

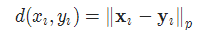
十六、连接时序分类损失 CTCLoss

连接时序分类损失（Connectionist Temporal Classification Loss，CTCLoss）是一种用于训练时序分类模型（如语音识别、文本识别等）的损失函数。它解决了时序数据对齐与标签对齐之间的问题，允许模型在训练过程中学习对不确定的对齐进行建模。

CTCLoss的计算方式基于前向-后向算法（Forward-Backward Algorithm）和动态规划的思想，用于计算模型预测序列和真实标签序列之间的对齐成本。

CTCLoss的主要步骤如下：

1. 预测：模型生成一个输出序列，通常使用Softmax函数将输出映射到概率分布。
2. 对齐：使用对齐算法（如束搜索、动态规划等）将预测序列与真实标签序列对齐，考虑到不同长度和对齐的可能性。
3. 成本计算：计算对齐序列的成本，即模型预测序列与真实标签序列之间的差异。
4. 损失计算：将成本转化为损失值，通过最小化损失值来调整模型的参数。

CTCLoss的优点是它不需要对齐预测序列和标签序列，而是通过计算所有可能的对齐方式的平均成本来训练模型。这使得模型能够学习到更好的对齐模式，并对不完全对齐的数据具有鲁棒性。

通过最小化CTCLoss来调整模型的参数，可以使模型在时序分类任务中更好地学习到数据的时序特征，并提高分类准确性。CTCLoss在语音识别、文本识别等领域得到了广泛的应用。

CTC连接时序分类损失，可以对没有对齐的数据进行自动对齐，主要用在没有事先对齐的序列化数据训练上。比如语音识别、ocr识别等等。

torch.nn.CTCLoss(blank=0, reduction='mean')

参数：

reduction-三个值，none: 不使用约简；mean:返回loss和的平均值；sum:返回loss的和。默认：mean。

十七、负对数似然损失 NLLLoss

负对数似然损失（Negative Log-Likelihood Loss，NLLLoss）是一种常用的损失函数，用于多类别分类任务中的概率建模。它基于最大似然估计的原理，鼓励模型预测正确类别的概率尽可能高。

NLLLoss的计算方式如下：
NLLLoss = -log(p(y))

其中，p(y)表示模型预测样本属于真实类别y的概率。

NLLLoss通过计算正确类别的对数概率的负值来衡量模型预测的不确定性。当模型对正确类别的概率越高时，NLLLoss的值越低，表示模型的预测越准确。

在多类别分类任务中，NLLLoss通常与Softmax函数结合使用。模型通过Softmax函数将预测得分转化为概率分布，并使用NLLLoss来计算预测概率与真实标签之间的差异。

通过最小化NLLLoss来调整模型的参数，可以使模型在训练过程中更好地拟合训练数据，并提高分类准确性。NLLLoss在许多机器学习任务中得到了广泛的应用，特别是在多类别分类和概率建模问题中。

负对数似然损失. 用于训练 C 个类别的分类问题。

torch.nn.NLLLoss(weight=None, ignore_index=-100,  reduction='mean')

参数：

weight (Tensor, optional) – 自定义的每个类别的权重. 必须是一个长度为 C 的 Tensor

ignore_index (int, optional) – 设置一个目标值, 该目标值会被忽略, 从而不会影响到 输入的梯度。

十八、NLLLoss2d

"NLLLoss2d"并不是标准的损失函数名称，可能是一个自定义的损失函数或者特定库中的命名。一般情况下，NLLLoss（负对数似然损失）用于多类别分类任务，而"NLLLoss2d"可能是指在特定情况下应用NLLLoss的二维版本。

在某些场景下，输入数据可能是二维的，例如图像分割任务中的像素级分类。在这种情况下，"NLLLoss2d"可能是指将NLLLoss应用于二维空间的每个像素。这种损失函数的计算方式与标准的NLLLoss类似，但是适用于二维空间中的分类任务。

具体而言，对于二维图像分割任务，每个像素都有一个真实类别标签，并且模型会对每个像素预测一个概率分布。"NLLLoss2d"将计算每个像素的NLLLoss，并对所有像素的损失值进行求和或平均。这样做的目的是鼓励模型对每个像素都产生准确的分类概率，并在整个图像上进行一致的分割预测。

需要注意的是，如果你使用的是特定的深度学习库或框架，建议查阅其文档以了解"NLLLoss2d"的具体含义和使用方式，以便正确地使用该损失函数。

对于图片输入的负对数似然损失. 它计算每个像素的负对数似然损失。

torch.nn.NLLLoss2d(weight=None, ignore_index=-100, reduction='mean')

参数：

weight (Tensor, optional) – 自定义的每个类别的权重. 必须是一个长度为 C 的 Tensor

reduction-三个值，none: 不使用约简；mean:返回loss和的平均值；sum:返回loss的和。默认：mean。

十九、PoissonNLLLoss

PoissonNLLLoss是一种用于训练计数数据模型的损失函数，通常用于处理具有Poisson分布特性的数据。它衡量模型的预测与真实计数值之间的差异，并鼓励模型学习生成接近真实计数分布的预测结果。

PoissonNLLLoss的计算方式如下：
PoissonNLLLoss = exp(ŷ) - y * ŷ

其中，ŷ表示模型对计数样本的预测值，y表示真实的计数值。

PoissonNLLLoss基于Poisson分布的对数似然函数推导而来。它的目标是最小化模型预测的对数似然损失，以便模型能够更好地拟合计数数据的分布特性。

PoissonNLLLoss的优点是它适用于计数数据的建模，例如自然语言处理中的文本词频、生物学中的基因表达计数等。通过最小化PoissonNLLLoss来调整模型的参数，可以使模型学习到适合计数数据的分布特征，从而提高模型的性能。

如果你在使用特定的深度学习库或框架，建议查阅其文档以了解PoissonNLLLoss的具体实现和使用方式，以便正确地应用该损失函数。

目标值为泊松分布的负对数似然损失：

torch.nn.PoissonNLLLoss(log_input=True, full=False,  eps=1e-08,  reduction='mean')

参数：

log_input (bool, optional) – 如果设置为 True , loss 将会按照公 式 exp(input) - target * input 来计算, 如果设置为 False , loss 将会按照 input - target * log(input+eps) 计算。

full (bool, optional) – 是否计算全部的 loss, i. e. 加上 Stirling 近似项 target * log(target) - target + 0.5 * log(2 * pi * target)。

eps (float, optional) – 默认值: 1e-8