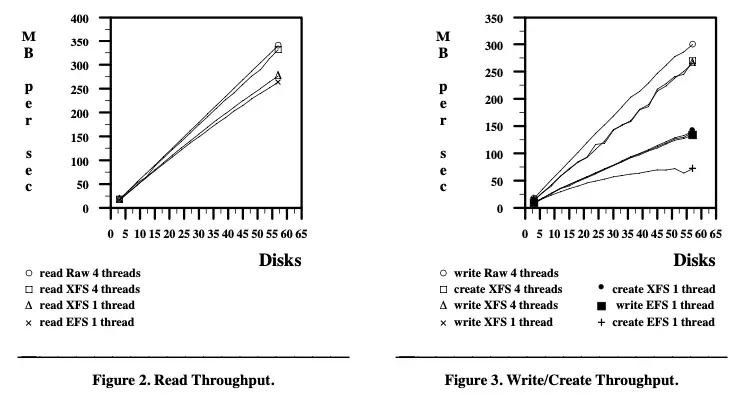
第四章 串

串：限定数据元素类型的线性表。
应用实例：
编辑软件(本质上是字符串处理)
信息检索、病毒查找(字符串比较)
第一节 逻辑结构

一、定义

串是由字符组成的线性表。
STRING=(D，S，P)
D = {ai| ai∈CHARACTER(字符集), i=0,1,2,…,n-1}
ASCII码串: CHARACTER为ASCII码字符集。
位串：CHARACTER={0,1}
S = {<ai-1,ai>| ai-1,ai∈D, i=1,2,…,n-1}
"a0a1……an-1"的长度为n。
空串：长度为0。
子串：串中任意个连续字符组成的子序列。
两串相等：两串长度相等，对应的每个字符相等。
例：根据字符串比较运算的定义，完善该函数：
int strcmp(char s[ ], char t[ ])
{ int i;
for (i=0; s[i] && t[i]; i++)
if (s[i]!=t[i]) ;
; }

二、基本运算

赋值 StrAssign(&S,T)
判断 StrEmpty(S) StrComp(S,T)
求长度 StrLen(S)
联接 Concat(&T,S1,S2)
求子串 SubStr(&Sub,S,pos,len)
子串定位Index(S,T,pos)
替换 Replace(&S,T,V)
插入 StrInsert(&S,pos,T)
删除 StrDelete(&S,pos,len)
释放 DestroyString(&S)

第二节 存储结构

一、顺序存储

串中相邻的字符存放在内存的相邻单元中。


优点：访问子串方便，
缺点：空间大小不灵活，插入、删除费时。

二、链式存储

如何设置结点的大小？
一个结点存储1个字符：非紧缩格式。
空间浪费，操作简单。
一个结点存储多个字符：紧缩格式。
空间效率高，操作复杂。

如何在紧缩格式的链串中插入、删除？

第三节 模式匹配

模式匹配Index(S, T, pos)
主串S中寻找模式串T的起始位置。
pos是主串中进行模式匹配的起始位置。
Index(“abcdef”,“cde”)：2
Index(“abcdef”,“ab”) ：0
Index(“abcdef”,“ad”) ：-1

一、BF算法(Brute-Force)
主 串S=“s0s1…sm-1”
模式串T=“t0t1…tn-1”
匹配过程：

匹配结果：

int index_BF(char s[],char t[])
{ int i=0,j=0;
while(s[i] && t[j])
if(s[i]==t[j]) { i++; j++; }
else { i=i-j+1; j=0; }
if(t[j]==0) return(i-j);
else return(-1);
}
问题分析：
S=“aaaaaaaaaaaaaaab” 长度为m
T=“aaaab” 长度为n
回溯次数=m-n
最差时间复杂度：O((m-n)n) ≈ O(nm)
再例：S=“abcabcabcde”
T=“abcabcd”

二、KMP算法(Knuth等3人)

1、推导

琢磨模式串的内在规律，使得：
在si<>tj时，i不回溯，j适当回溯，再重新比较。
当si<>tj时，i不变，j=k。 求k=？ (k<j)
此时有： “t0t1…tj-1”=“si-j…si-1”

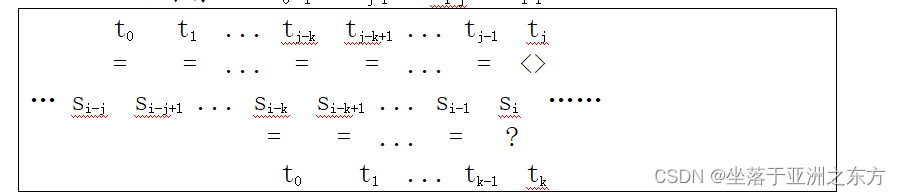
显然，k应具有性质：
“t0t1…tk-1”=“si-k…si-1”=“tj-ktj-k+1…tj-1”
即：“t0t1…tk-1”=“tj-ktj-k+1…tj-1”
即：当tj与si失配时，由于tj的前k个字符等于模式串的开头k个字符,所以可将si与tK比较。
为达到更高效率，k越大越好。(k<j)
2、next[]
每个tj与对应一个k值，所以设立next[]存储所有k值。
计算方法：
1、j=0时：next[j]=-1;
2、存在"t0t1…tk-1"=“tj-ktj-k+1…tj-1”，(k<j)：
例如：“t0”=“tj-1” “t0t1”=“tj-2tj-1” “t0t1t2”=“tj-3tj-2tj-1”
next[j]=max(k)。
3、否则：next[j]=0;
3、KMP程序
//预先求出next[]
int index_kmp(char s[],char t[],int next[])
{int i=0, j=0;
while(s[i] && t[j])
if(j==-1 || s[i]==t[j]) { i++; j++; }
else j=next[j];
if(t[j]0) return(i-j);
else return(-1);
}
体会j-1
体会j=next[j]
例1： a b c a b c d
-1 0 0 0 1 2 3

例2： a a a a b
-1 0 1 2 3

例：设主串s=“abcabcabd”，模式串p=“abcabd”，按KMP算法进行模式匹配，当"s0s1s2s3s4"=“p0p1p2p3p4”，且s5≠p5时，应进行 比较。
A、s5和p2 B、s5和p3 C、s1和p0 D、s8和p5

第四节 串操作实例

一、文本编辑软件的数据结构

1、文本编辑软件

数据对象：字符串。

基本操作：插入、删除字符。
简易文本编辑器的功能菜单：
①末尾添加/在某行前插入一行；
②删除指定行；
③在某行中插入字符串；
④在某行中删除某子串；
⑤查找/替换子串；
⑥打开/保存文件；
⑦显示文件内容（可以简化）

2、数据结构的设计

如何减少时间/空间复杂度？
方案①：整个文件是一个顺序/链式字符串。
方案②：每行作为一个顺序/链式字符串，
行表：所有行结构的头结点组成的线性表。
行表的存储结构：顺序/链式
顺序结构：字符数/行、行数有上限
链式结构：存储空间浪费严重。
紧缩格式？

二、多模式匹配问题：网络搜索引擎、病毒搜索

查找对象：一个大字符串S
若干模式串：一个字符串集合Keywords
S中存在多个包含Keywords中所有关键字的匹配子串。
目标：求出包含所有匹配子串的最短匹配子串。
上机：

1、模式匹配

例1、子串替换
main()
{ char s[M]=“abcdeabcdef”,t[M]=“bcde”;
char v[M]=“12”; // “1234” “123456” “”
substr(s,t,v); puts(s);
}
将s[]中的t[]用v[]替换
void substr(char s[],char t[],char v[])
{ int s_len,t_len,v_len,s_i,t_i,v_i,gap,i,j;
s_len=strlen(s); t_len=strlen(t); v_len=strlen(v);
gap=v_len-t_len;
s_i=0;
while( s[s_i] )
{ for(t_i=0; s[s_i] && t[t_i]; ) //　定位
if(s[s_i]t[t_i]) { s_i++; t_i++; }
else { s_i=s_i-t_i+1; t_i=0; }
if(t[t_i]‘\0’) // 替换
{ if(gap>0)　 // 扩充s串
for(i=s_len-1; i>=s_i; i–) s[i+gap]=s[i];
if(gap<0)　　// 缩减s串
for(i=s_i; i<=s_len-1; i++) s[i+gap]=s[i];
for(i=s_i-t_len,j=0; j<v_len; i++,j++)s[i]=v[j];
s_len=s_len+gap;
s_i=s_i+gap;
}
}
s[s_len]=‘\0’;
}
例2、在结点大小为1的链串上，实现子串定位算法。若匹配成功，则返回起始结点地址，否则返回空指针。
typedef struct lstring
{ char data;
struct lstring *next;
}LString;

LString *index_BF(LString *s, LString *t)
{ LString *sp, *tp, *sstart;
sp=s; tp=t; sstart=s;
while(sp && tp)
{ if(sp->data==tp->data)
{ sp=sp->next; tp=tp->next; }
else { sstart=sstart->next; sp=sstart; tp=t; }
}
if(!tp) return(sstart);
else return(NULL);
}

第五章 数组和广义表

继续增加线性表结构的内涵。

第一节 数组的逻辑结构

1_Array=(D, S, P)　定长线性表

D = {ai| ai∈ElemSet, i=0,1,2,…, n-1}
S = {<ai-1,ai>| ai-1,ai∈D, i=1,2,…,n-1}
2_Array=(D, S, P) 定长线性表，每个元素又是定长线性表。

D = {ai,j| ai,j∈ElemSet, i=0,1,…,n1-1; j=0,1,…,n2-1}
S = {ROW,COL}
ROW={<ai,j-1, ai,j>| i=0,1,…,n1-1; j=1,…,n2-1}
COL={<ai-1,j, ai,j>| i=1,…,n1-1; j=0,1,…,n2-1}
3_Array=(D, S, P) 增加层的关系
二维数组：分量为一维数组的一维数组。
三维数组：分量为二维数组的一维数组。
数组一旦被定义，它的维数和维界就不再改变。
基本操作：取值、赋值。

第二节 数组结构的顺序存储结构

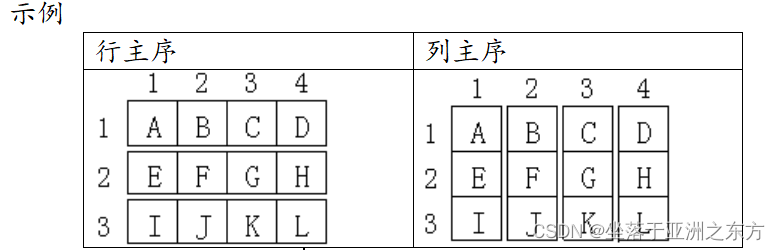
数组结构是多维的，内存地址是一维的。
二维数组a[n1][n2]的存储方式：

1、初始化数组结构

Status Array_Init(Array &A,int dim,int bounds[])
{ A.dim=dim;
A.bounds= (int )malloc(dimsizeof(int));
A.constants=(int )malloc(dimsizeof(int));
if(!A.bounds || !A.constants) return(OVERFLOW);
for(i=0;i<dim;i++) A.bounds[i]=bounds[i];
for(A.constants[dim-1]=1,i=dim-2; i>=0; i–)
A.constants[i]=A.bounds[i+1]*A.constants[i+1];
//开辟数组空间
elemtotal=A.bounds[0]*A.constants[0];
A.base=(ElemType )malloc(elemtotalsizeof(ElemType));
if(!A.base) return(OVERFLOW);
return(OK);
}

2、取值

ElemType Array_GetValue(Array A,int dim_i[])
{ int offset;
for(offset=0,i=0; i<A.dim; i++)
offset+=A.constants[i] * dim_i[i];
return(*(A.base+offset));
}

main()
{ Array A; ElemType e;
int bounds[4]={3, 4, 5, 6};
int dim[4]={2,1,3,4};
Array_Init(A, 4, bounds);
…
e = Array_GetValue(A,dim);
}

第三节 矩阵的压缩存储

矩阵的用途：
大型方程组求解、高次方程求解
真正有用的计算是矩阵的计算。
从空间/时间复杂度出发，讨论矩阵的存储结构。

一、特殊矩阵

利用矩阵的特征，尽量减少数据的存储量。

1、对称矩阵 aij=aji

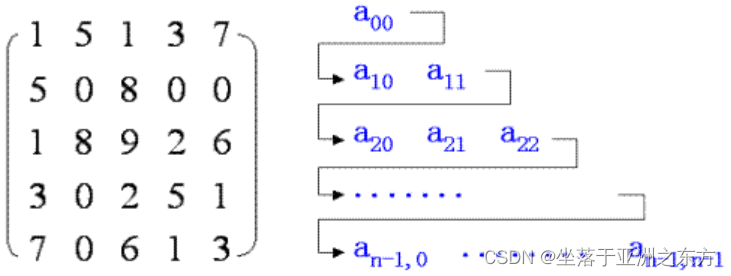
NxN矩阵的存储结构：S[N(N+1)/2]。
以行主序的方式存储下三角元素：
若i>=j: k=i*(i+1)/2+j
若i< j: k=j*(j+1)/2+i
/* 取值 /
int getValue(int i,int j)
{ if(i>=j) return(s[i(i+1)/2+j])
else return(s[j*(j+1)/2+i]);
}
/* 赋值 /
void SetValue(int i,int j,int e)
{ if(i>=j) s[i(i+1)/2+j]=e;
else s[j*(j+1)/2+i]=e;
}

2、上/下三角矩阵

类似对称矩阵。只是某个三角区域的所有元素为0，或某个固定值。
例：设N阶对称矩阵A存储为一维数组S[N(N+1)/2]，以行主序的方式存储A的下三角，则元素A[3][5]的存储位置是？

3、小结

练习的意义：培养摸索数据规律的感觉。

二、稀疏矩阵之三元组表

稀疏因子=t/(m*n)
稀疏矩阵：稀疏因子<=0.05的大型矩阵。（非0数很少，且无规律）

1、三元组的顺序表

约定：①三元组中的e必须不等于0。
②非0元素按行主序排列。
优点：节省空间。
缺点：按行号、列号存取元素，费时。

2、转置运算 M=>T (以T为中心，按需点菜)

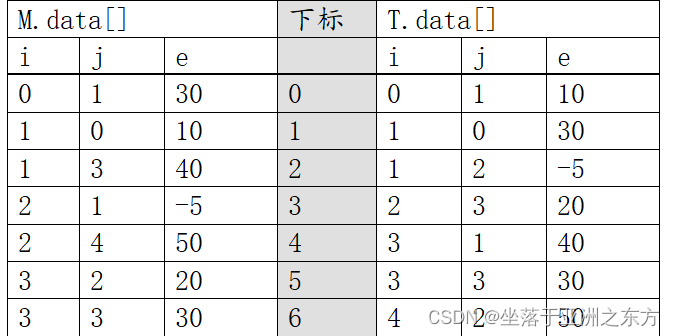
void TSMatrix_Transpose(TSMatrix M,TSMatrix &T)
{ int k,col,i;
T.mu=M.nu; T.nu=M.mu; T.tu=M.tu;
for(k=0,col=0; col<M.nu; col++) //找M中所有列
for(i=0; i<M.tu; i++)
if(M.data[i].j==col)
{ T.data[k].i=M.data[i].j;
T.data[k].j=M.data[i].i;
T.data[k].e=M.data[i].e; k++;
}
}
时间复杂度：
若M有n列，有t个非0数：为O(nt)。
若t≈mn： 为O(nmn)。

3、快速转置运算 M=>T (以M为中心，按位就座)

辅助数据结构：
num[]：M中每列(T中每行)的三元组个数。
=》pos[]：T中每行第一个三元组的下标。
pos[0]=0;
pos[j]=pos[j-1]+num[j-1]; j∈[1,M.nu-1]


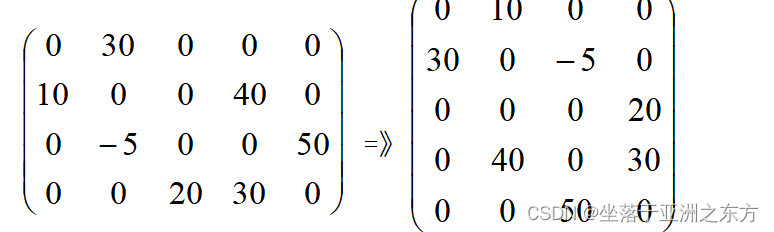
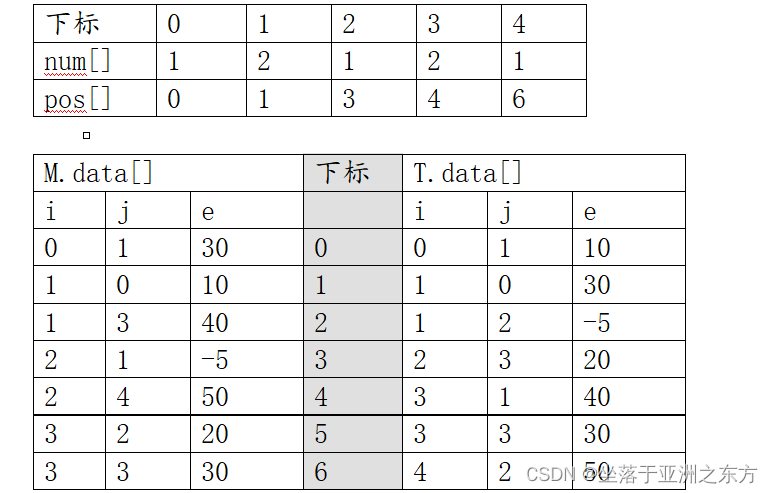
void TSMatrix_FastTranspose(TSMatrix M,TSMatrix &T)
{ int i,j,k,num[MAX],pos[MAX];
T.mu=M.nu; T.nu=M.mu; T.tu=M.tu;
//统计M中每列的三元组个数
for(i=0;i<M.nu;i++) num[i]=0;
for(i=0;i<M.tu;i++) num[M.data[i].j]++;
//计算pos数组
for(pos[0]=0,i=1;i<M.nu;i++)
pos[i]=pos[i-1]+num[i-1];
//快速转置
for(i=0;i<M.tu;i++)
{ col=M.data[i].j; loc=pos[col];
T.data[loc].i=M.data[i].j;
T.data[loc].j=M.data[i].i;
T.data[loc].e=M.data[i].e; pos[col]++;
}
}
时间复杂度：
若M有n列，有t个非0数：循环次数：n+t+n+t
若t≈mn： 为O(mn)。
空间复杂度：2个数组(n+n个单元)，O(n)。
人生的启迪：
了解、把握已有的财富，比眼望着目标更有效！

4、三元组表小结

如何快速定位呢？==>十字链表。

三、稀疏矩阵之十字链表

十字链表的存储结构：真正等价于矩阵的逻辑结构。

1、十字链表

图示：4x5矩阵的十字链表，含非0数：
(1,1:1) (3,1:2) (3,4:3)
用right构成行链表，用down构成列链表。

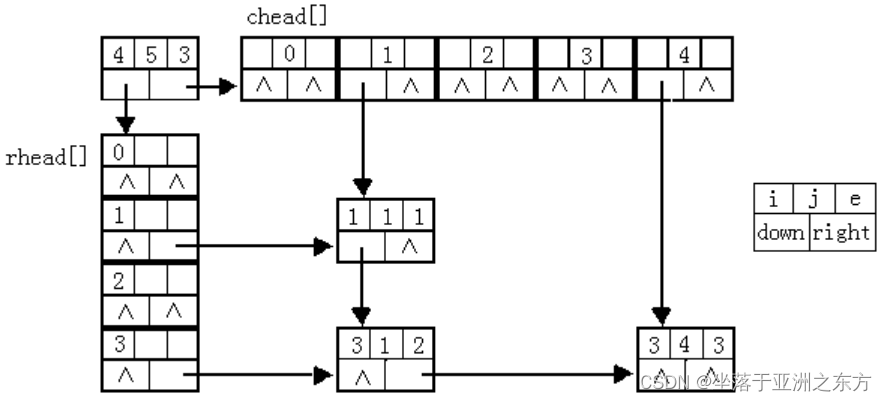
2、建立、打印十字链表的算法

按行主序打印矩阵M
void CrossList_Print(CrossList M)
{ OLNODE *p; int i;
printf(“%d,%d,%d\n”,M.mu,M.nu,M.tu);
for(i=0; i<M.mu; i++)
for(p=M.rhead[i].right; p!=NULL; p=p->right)
printf(“%d,%d:%d\n”,p->i,p->j,p->e);
}
根据三元组顺序表T，建立十字链表M
void CrossList_Create(CrossList &M, TSMatrix T)
{ int i;
CrossList_Init(M,T.mu,T.nu);
for(i=0; i<T.tu; i++) // 插入各个三元组结点
CrossList_Insert(M, T.data[i]);
}
初始化十字链表结构M
void CrossList_Init(CrossList &M,int mu,int nu)
{ int i;
M.mu=mu; M.nu=nu; M.tu=0;
//初始化行头结点表、列头结点表
M.rhead=(OLNODE )malloc(M.musizeof(OLNODE));
for(i=0; i<M.mu; i++) M.rhead[i].right=NULL;
M.chead=(OLNODE )malloc(M.nusizeof(OLNODE))
for(i=0; i<M.nu; i++) M.chead[i].down=NULL;
}
根据三元组Item，新建结点，并插入十字链表M中
void CrossList_Insert(CrossList &M, Triple Item)
{ OLNODE *newp,*p,pre;
// 插入行链表中
for(pre=&M.rhead[Item.i],p=pre->right;p; pre=p,p=p->right)
if(p->j >= Item.j) break; // 定位
if(pNULL || p->j > Item.j)
{ newp=(OLNODE *)malloc(sizeof(OLNODE));
newp->i=Item.i; newp->j=Item.j; newp->e=Item.e;
newp->right=p; pre->right=newp; M.tu++;
}
else // 遇到同类项
{ p->e+=Item.e;
if(p->e0) pre->right=p->right;
}
// 将new结点插入列链表中
for(pre=&M.chead[Item.j],p=pre->down; p; pre=p,p=p->down)
if(p->i >= Item.i) break; // 定位
if(pNULL || p->i > Item.i)
{ newp->down=p; pre->down=newp; }
else // 遇到同类项
if(p->e0) { pre->down=p->down; free§; M.tu–}
}

第四节 广义表的逻辑结构

一、定义

线性表的扩展，每个元素的结构不等。
GList={a1,a2,…,an | ai∈AtomSet或ai∈GList}
ai∈AtomSet：ai为原子
ai∈Glist ：ai为子表

数据关系：顺序关系、层次关系。
a1为表头(head)元素, 其余为表尾(tail)。
应用实例：Lisp语言、前缀表达式
(setq x (+ 4 (- a b)) y (+ 3 4) )
表头：函数名； 表尾：参数表

二、基本操作

求长度：GList_Length(L)
求深度: GList_Depth(L) 表的最大层次数
原子深度=0，表深度=max{GList_Depth(ai)}+1
例：求长度、深度：
(a), (), ((a),a)， (((a),a),(a),a)
遍历表：Glist_Traverse(L)
复制表：Glist_Copy(L,&T)
取表头：GList_Head(L)
取表尾：GList_Tail(L)
取第i个元素：GList_nth(L,i)

第五节 广义表的存储结构

一、不规范的结构图

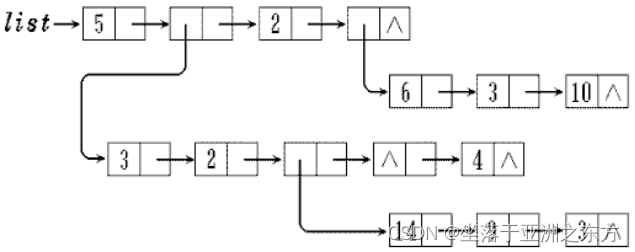
二、广义表的存储结构

二种结点：表结点、原子结点

结构约定：所有广义表带特殊头结点(相当于括号)。
能简化算法。
绘制存储结构：

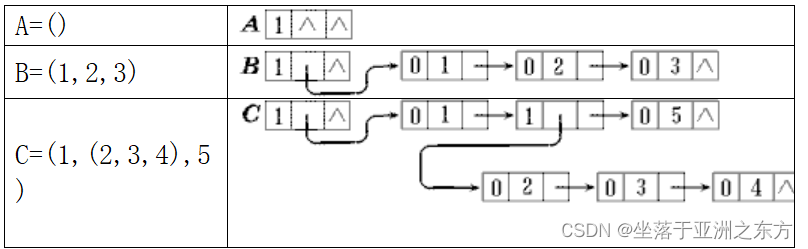
第六节 m元多项式的存储

绘制存储结构

F(x,y,z)=((x12+2x6)y3+(3x15)y2)z20 + ((x18+6x3)y4+2y)z10 + 15
第七节 广义表的递归算法
typedef char AtomType;
typedef enum {ATOM,LIST} ElemTag;
typedef struct GLNode
{ ElemTag tag;
union
{ AtomType atom;
struct GLNode *child;
}UNION;
struct GLNode *next;
}GLNODE;

一、遍历广义表，打印层次括号

void GList_Traverse(GLNODE *L)
{ GLNODE *p;
putch(‘(’);
for(p=L->UNION.child; p; p=p->next)
if(p->tag==ATOM) printf(“%c “,p->UNION.atom);
else // 特殊头结点等价于”( )”
{ putch(‘(’);
GList_Traverse(p->UNION.child);
putch(‘)’);
}
putch(‘)’);
}

二、求表深度

int GList_Depth(GLNODE *L)
{ GLNODE *p;
int depth1, max=0;
if(L->tag==ATOM) return(0);
for(p=L->UNION.child; p; p=p->next)
{ depth1=GList_Depth§;
if(depth1>max) max=depth1;
}
return(max+1);
}

第六章 树

第一节 树的定义

一、逻辑结构

树结构：层次关系、线性关系。
例1：资源管理器；
例2：个人照片管理；
树的逻辑结构图：

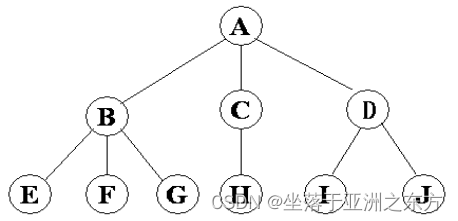
通俗定义：

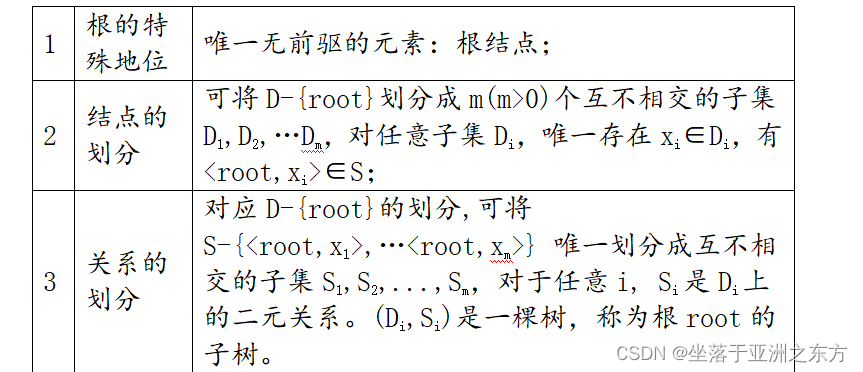
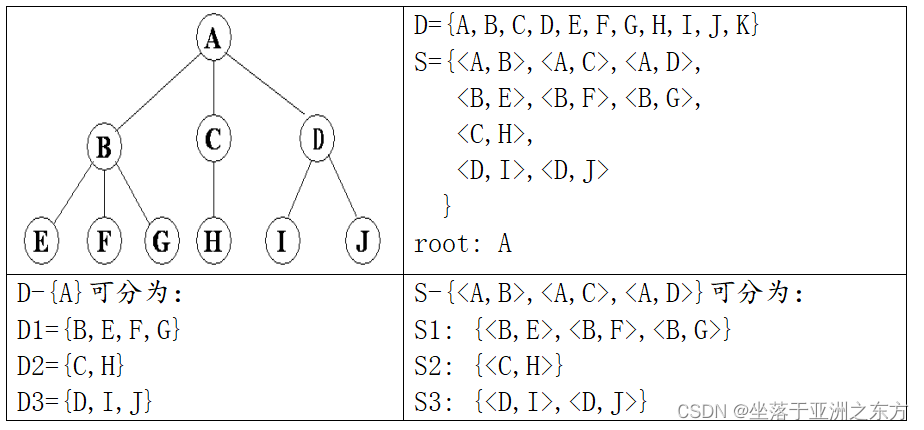
树是n(n>0)个结点的有限集，在任意一棵树中：
1)有且只有一个特定的根(root)结点；

2)当n>1时，其余结点可分为m(m>0)个互不相交的有限子集T1,T2…Tm，每个子集是一棵树，称为子树。
形式定义：
Tree=(D,S,P)
D={ai | ai∈ElemSet，i=1,2,…,n}
二元关系S：
当n=1时，S=φ；
当n>1时：

二、术语

三、基本逻辑操作

第二节 二叉树

一、定义

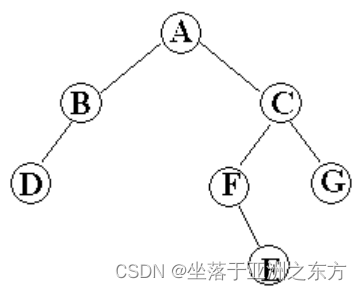
形式定义：参考树的定义。
根结点、左子树、右子树。
二叉树的逻辑结构图：

二、二叉树的形态

具有3个结点的二叉树，有哪些形态？

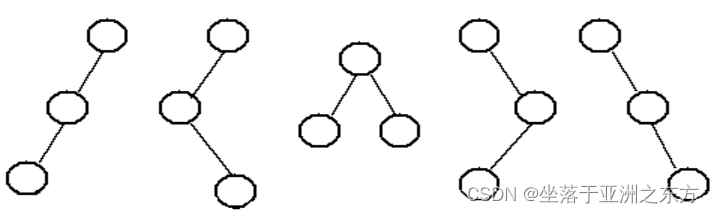
具有n个结点的二叉树，有多少种形态？
例：n个结点的相似树的个数
int TCount(int n)
{ int left,count=0;
if(n0 || n1) return(1);
for(left=n-1; left>=0; left–)
count+=TCount(left)*TCount(n-1-left);
return(count);
}
计算：TCount(5)=？

三、性质

基本常识：关系数=结点数-1

性质1：若一个二叉树，叶子结点数为n0，度为2的结点数为n2,

则n0=n2+1。
例：若一棵树中度为1的结点有N1个，度为2的结点有N2个，……，度为m的结点有Nm个，则该树的叶结点有 (N1+2N2+…+mNm+1)-(N1+N2+…+Nm) 个。

性质2：二叉树的第i层上的结点数最多为2i-1。

性质3：深度为k的二叉树中结点总数最多为2k-1。

满二叉树：　深度为K的二叉树。共有2k-1个结点。
完全二叉树：深度为K的二叉树，前k-1层是满二叉树，
第k层的结点从左至右依次排列。


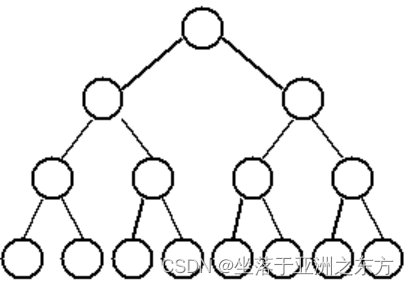
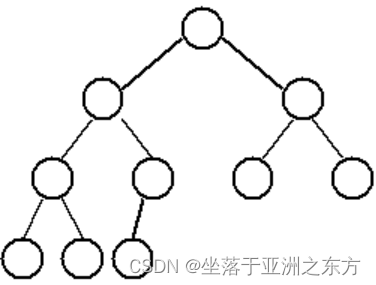
性质4：具有n个结点的完全二叉树的深度为int(log2n)+1。
性质5：有n个结点的完全二叉树，结点从0顺序标号，则：

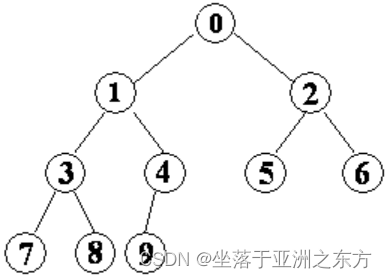
1、若i>0，i的双亲结点是(i-1)/2。
2、若2i+1<n，i的左孩子是2i+1；若2i+1>=n，i无左孩子。
3、若2i+2<n，i的右孩子是2i+2；若2i+2>=n，i无右孩子。

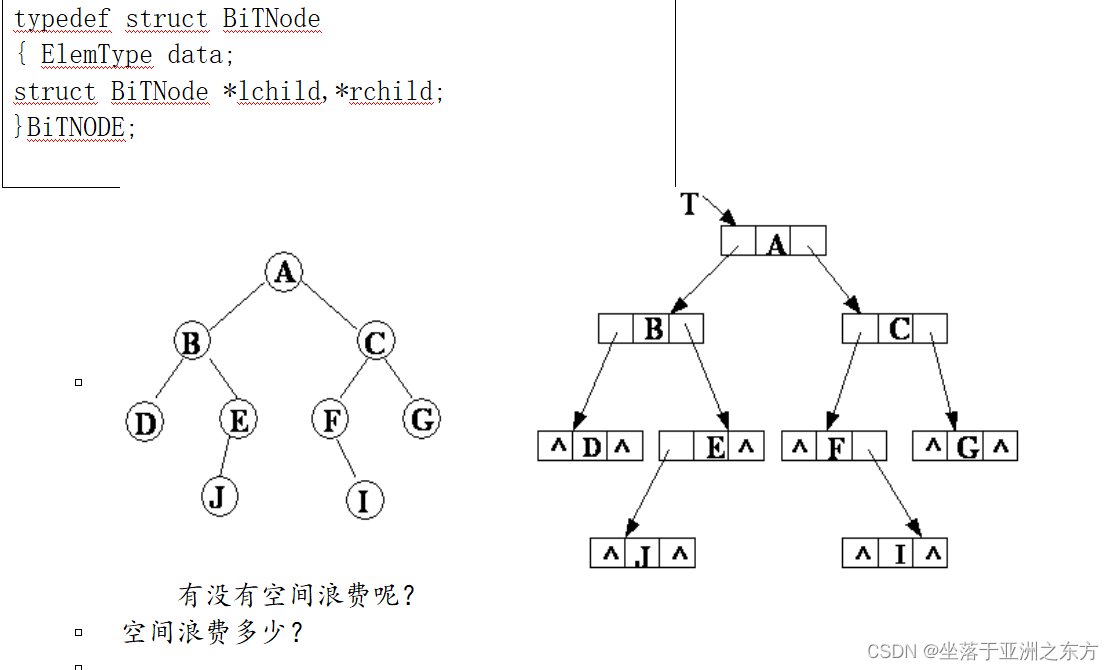
四、存储结构

1、顺序结构

依照满二叉树的结点顺序，存放各个结点。
存储位置暗藏树的关系。
例：将68个结点的完全二叉树，按顺序存储结构存于数组A[0…100]中，叶子结点的最小编号是 。
A、32 B、33 C、34 D、35
例：具有101个结点的完全二叉树，其度为1的结点有 个。
分析：
满/完全二叉树：存储效率最高，插入、删除方便。
非完全二叉树 ：


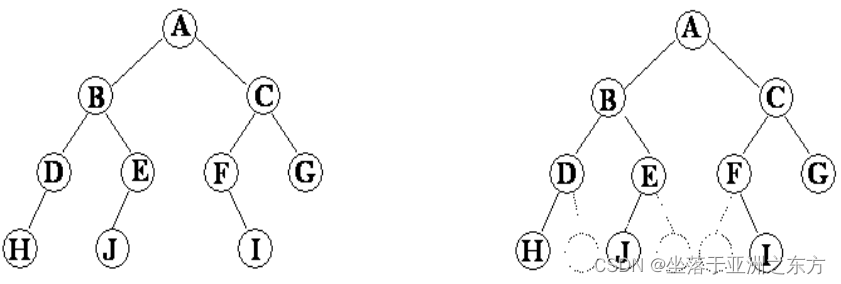
不存在的结点，用特殊符号标识。
空间浪费大，不灵活。
退化的二叉树：

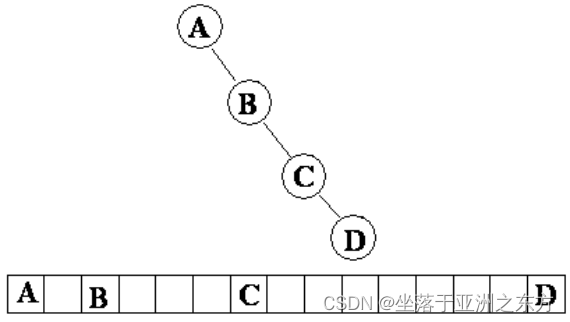
链式结构(二叉链表结构)

第三节 遍历二叉树

遍历：每个结点访问且只访问一次。

一、深度遍历(递归)：先序、中序、后序

二叉树 = 根结点 + 左子树 + 右子树
将树的遍历转变为子树的遍历。

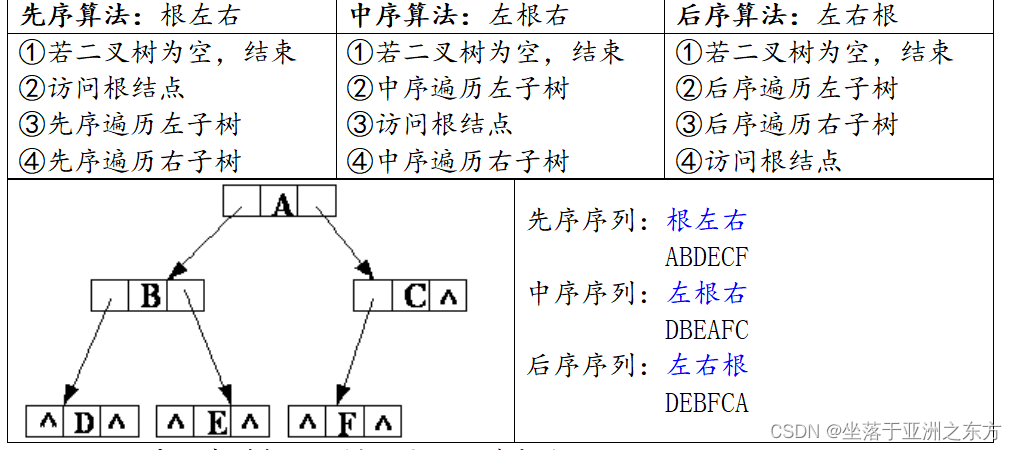
遍历序列与二叉树不是一一对应的。
例：若前序序列为123，对应的二叉树有5种。

思考：试找出分别满足下列条件的所有二叉树
①先序序列和中序序列相同
②中序序列和后序序列相同
③先序序列和后序序列相同
void BiT_PreOrder(BiTNODE *root)
{①if(root==NULL) return;
②printf(“%d,”,root->data);
③BiT_PreOrder(root->lchild);
④BiT_PreOrder(root->rchild);
}
跟踪程序：观察调用栈Ctrl-F3。

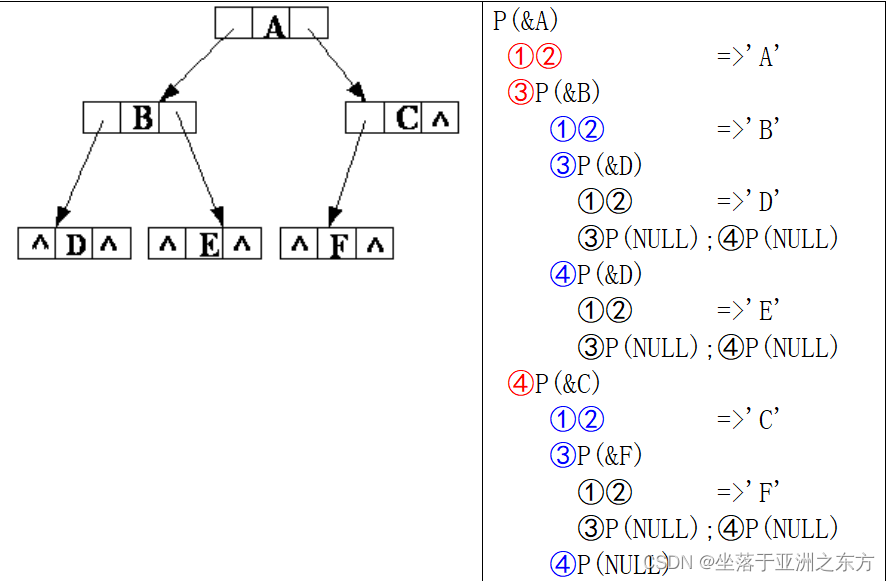
逻辑清晰，效率不高。
时间复杂度：结点数为n, O(n)
空间复杂度：栈的深度=树的深度k, O(k)

二、层次(广度)遍历二叉树

1、算法

①将根指针加入队列；
②取队首元素，设为p；访问结点p；
③若p存在左孩子，将其加入队列；
若*p存在右孩子，将其加入队列；
④若队列不空，则循环②③，否则完成。
void BiT_TravelByLevel(BiTNODE *root)
{ BiTNODE p; Queue Q; / Q为指针队列 /
if(root==NULL) return;
Queue_Init(Q); / 初始化队列 /
Queue_Enter(Q, root); / 将root进队列 /
while(!Queue_Empty(Q))
{ p=Queue_Leave(Q); / 出队列的值赋给p /
printf(“%d,”, p->data); / 每个元素出队列一次 */
if(p->lchild) Queue_Enter(Q,p->lchild);
if(p->rchild) Queue_Enter(Q,p->rchild);
}
}
时间复杂度：结点数为n, O(n)
空间复杂度：各层结点数的最大值
辅助程序
typedef struct queuenode
{ ElemType data;
struct Node *link;
}QueueNode;
typedef struct
{ QueueNode *front,*rear; }LinkQueue

三、遍历算法的应用

1、统计结点的个数

深度遍历模式
int BiT_Count(BiTNODE *root)
{ int left,right;
if(root==NULL) return(0);
left= BiT_Count(root->lchild);
right=BiT_Count(root->rchild);
return(1+left+right);
}

统计叶子结点的个数

int BiT_Count(BiTNODE *root)
{ int left,right;
if(rootNULL) return(0);
if(root->lchildNULL && root->rchild==NULL) return(1);
left= BiT_Count(root->lchild);
right=BiT_Count(root->rchild);
return(left+right);
}

层次遍历模式

int BiT_TravelByLevel(BiTNODE *root)
{ BiTNODE *p; int count=0;
Queue Q;
Queue_Init(Q);
Queue_Enter(Q, root);
while(!Queue_Empty(Q))
{ p=Queue_Leave(Q);
count++;
if(p->lchild) Q_Enter(Q,p->lchild);
if(p->rchild) Q_Enter(Q,p->rchild);
}
return(count);
}

思考：下列二叉树计数算法是否有错？

int count(BiTNODE *root)
{ int s=0;
if(root)
{ s++;
count(t->lchild);
count(t->rchild);
return(s);
}
}

2、求二叉树的深度

int BiT_Depth(BiTNODE *root)
{ int left,right;
if(root==NULL) return(0);
left =BiT_Depth(root->lchild)
right=BiT_Depth(root->rchild))
return(max(left,right)+1);
}
比较：广义表的深度算法

3、交换树中每个结点的左右子树

深度遍历模式
void BiT_Exchange(BiTNODE *root)
{ BiTNODE *p;
if(root==NULL) return;
BiT_Exchange(root->lchild);
BiT_Exchange(root->rchild);
p=root->lchild; root->lchild=root->rchild; root->rchild=p;
}

层次遍历模式

4、释放二叉树中的所有结点空间

深度遍历模式
void BiT_Free(BiTNODE root)
{ if(root==NULL) return;
BiT_Free(root->lchild); / 释放左子树 /
BiT_Free(root->rchild); / 释放右子树 /
free(root); / 按后序次序 */
}

层次遍历模式

void BiT_TravelByLevel(BiTNODE *root)
{ BiTNODE *p;
Queue Q;
Queue_Init(Q);
Queue_Enter(Q, root);
while(!Queue_Empty(Q))
{ p=Queue_Leave(Q);
if(p->lchild) Q_Enter(Q,p->lchild);
if(p->rchild) Q_Enter(Q,p->rchild);
free§;
}
}

5、在二叉树中查找关键值为key的结点

深度遍历模式

BiTNODE *BiT_Search(BiTNODE *root, int key)
{ BiTNODE *p;
if(rootNULL) return(NULL);
if(root->datakey) return(root);
p=BiT_Search(root->lchild, key);
if§ return§;
return( BiT_Search(root->rchild, key) );
}

层次遍历模式

BiTNODE *BiT_Search(BiTNODE *root, int key)
{ BiTNODE *p;
Queue Q;
Queue_Init(Q);
Queue_Enter(Q, root);
while(!Queue_Empty(Q))
{ p=Queue_Leave(Q);
if(p->data==key) return§;
if(p->lchild) Q_Enter(Q,p->lchild);
if(p->rchild) Q_Enter(Q,p->rchild);
}
return(NULL);
}

6、带空指针标记的先序序列=>二叉树

深度遍历模式

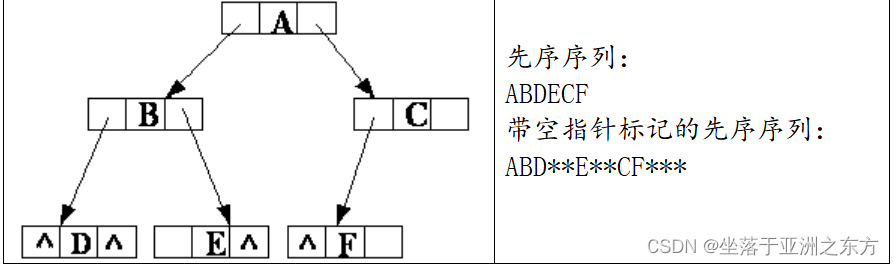
int i=0; //全局变量
main()
{ BiTNode root=BiT_Create("ABDECF**"); }

BiTNODE *BiT_Create(char s[])
{ BiTNODE root; char ch;
ch=s[i]; i++;
if(ch=='') return(NULL);
root=(BiTNODE )malloc(sizeof(BiTNODE));
root->data=ch;
root->lchild=BiT_Create(s); / 建左子树 /
root->rchild=BiT_Create(s); / 建右子树 */
return(root);
}

7、先序序列+中序序列=>二叉树

①讨论
二叉树和其遍历序列是否一一对应？
先序+中序=>二叉树
示例：先序: A B H F D E C K G
中序: H B D F A E K C G

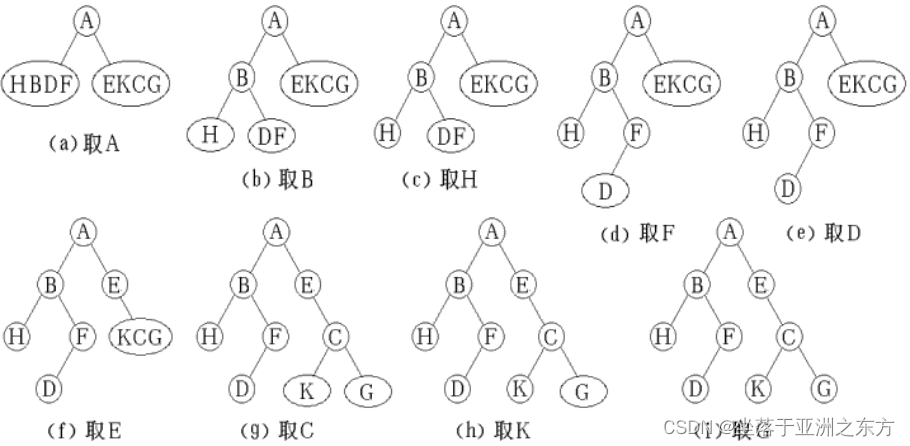
递归问题：分解策略，最终小问题的解决方案。
②算法
大小问题必须具有完全相同的形式。
BiTNODE *premid(char pre[],char mid[],int pre_i,int mid_i,int n)
{ int i; BiTNODE root;
if(n==0) return(NULL); / 最终解决方案 */
root=(BiTNODE )malloc(sizeof(BiTNODE));
root->data=pre[pre_i];
while(i=0; i<n; i++) / 在中序序列中定位根结点 */
if(pre[pre_i]==mid[mid_i+i]) break;
root->lchild=premid(pre,mid, pre_i+1, mid_i, i);
root->rchild=premid(pre,mid, pre_i+i+1,mid_i+i+1,n-i-1);
return(root);
}
后序+中序=>二叉树 OK
先序+后序=>二叉树 NO

8、实例：再论表达式的存储结构

字符串存储：识别运算符、运算数；比较优先级
=》效率低
①二叉树存储形式
运 算 符：分支结点；
运算对象：叶子结点；
左操作数：左子树；
右操作数：右子树；
例：a+b*c-d
②表达式树的结构
typedef enum {OP,OPD} TAG;
typedef struct node
{ TAG tag;
union
{ char op;
float data;
}UNION;
struct node *lchild,rchild;
}TNode;
③遍历的意义：求值
先序：前缀表达式
中序：中缀表达式
后序：后缀表达式
一次建树，多次高效计算、转换方便
float value(TNode root)
{ float x,y;
if(root->tag==OPD) return(root->UNION.data);
x=value(root->lch);
y=value(root->rch);
return(compute(root->UNION.op,x,y));
}
float compute(char op,float opd1,float opd2)
{ switch (op)
{ case ‘+’: return(opd1+opd2);
case ‘-’: return(opd1-opd2);
case '': return(opd1opd2);
case ‘/’: return(opd1/opd2);
}
}
作业与上机：
1、根据含空标志的先序序列，建立二叉树
2、根据先序序列、中序序列，建立二叉树
3、深度、层次遍历二叉树
4、统计结点的个数、二叉树的深度
5、在二叉查找关键值为x的结点

第四节 线索二叉树

如何快捷地找出结点的前驱、后继？
如何保存遍历过程得到的先后次序？
①每个结点增加前驱域、后继域。
②利用结点的空链域存储前驱域和后继域。

一、建立线索树

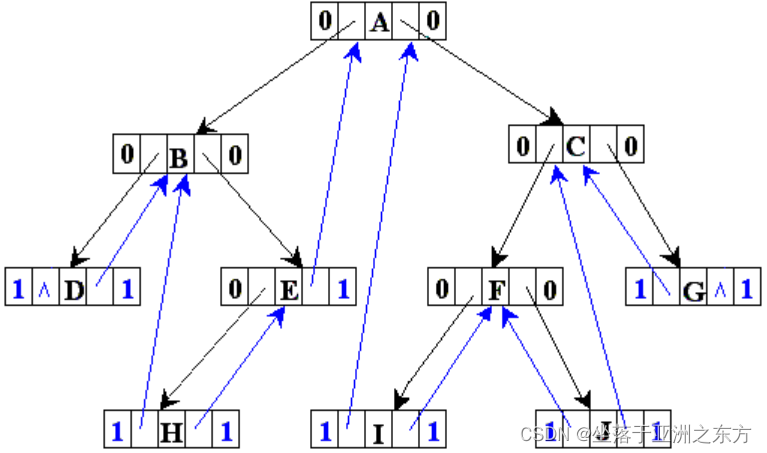
1、算法思路：

设root中所有结点的LTag、Rtag为LINK
①p遍历各结点，pre指向上一个访问的结点。
②每次指针变化前，线索化p的前驱，*prev的后继。

2、递归算法

BiTNODE *pre; //全局变量
void BiThrTree_MidOrderThread(BiTNODE *root)
{ if(rootNULL) return;
*pre=NULL;
BiThrTree_MidOrderThreading(root);
pre->rtag=THREAD; //最后遍历的是最右下的叶子
}
void BiThrTree_MidOrderThreading(BiTNODE *p)
{ if(pNULL) return;
if(p->LTagLINK)
BiThrTree_MidOrderThreading(p->lchild);
if(p->lchildNULL)
{ p->LTag=THREAD; p->lchild=pre; }
if(pre!=NULL && pre->rchildNULL)
{ pre->RTag=THREAD; pre->rchild=p; }
pre=p;
if(p->RTagLINK)
BiThrTree_MidOrderThreading(p->rchild);
}

二、检索结点(中序线索树)

如何在中序线索树中，找到指定结点*p的前驱、后继？

1、求*p的后继

若p->RTag=THREAD：后继为p->rchild
若p->RTag=LINK ：后继为p的右子树中最左下结点
BiThrNode * FindNext(BiThrNode *p)
{ if(p->rtagTHREAD) return(p->rchild);
for(p=p->rchild; p->ltagLINK; p=p->lchild);
return§;
}

2、求*p的前驱

若p->LTag=THREAD：前驱为p->lchild
若p->LTag=LINK ：前驱为p的左子树中最右下结点
BiThrNode * FindPrev(BiThrNode *p)
{ if(p->ltagTHREAD) return(p->lchild);
for(p=p->lchild; p->rtagLINK; p=p->rchild);
return§;
}

3、中序线索树中的遍历

// 不使用栈的中序遍历
void MidBiThrTree_Travel(BiThrNode *root)
{ BiThrNode p;
for(p=root; p->ltag==LINK; p=p->lchild); / 找到起点 */
for(; p; p=FindNext§) printf(“%d,”,p->data);
}
// 不使用栈的反中序遍历
void MidBiThrTree_ReverseTravel(BiThrNode *root)
{ BiThrNode p;
for(p=root; p->rtag==LINK; p=p->rchild); / 找到终点 */
for(; p; p=FindPrev§) printf(“%d,”,p->data);
}

第五节 树和森林

树逻辑结构=》二叉树存储结构、算法
=》树存储结构、算法。
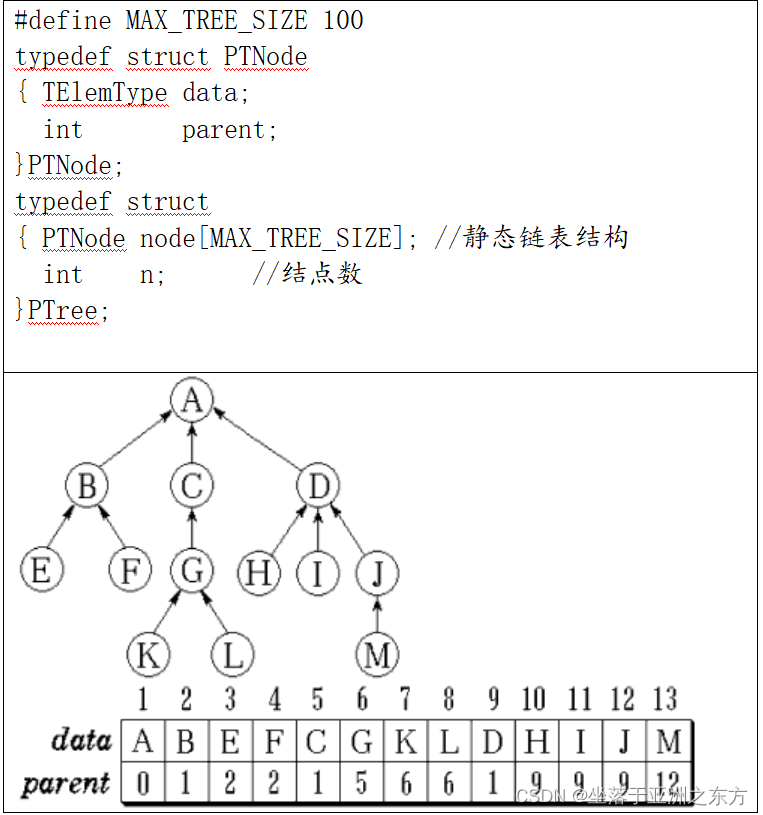
一、树的存储结构

1、双亲表示法

能否采用动态链表结构？

二、树与二叉树的转换

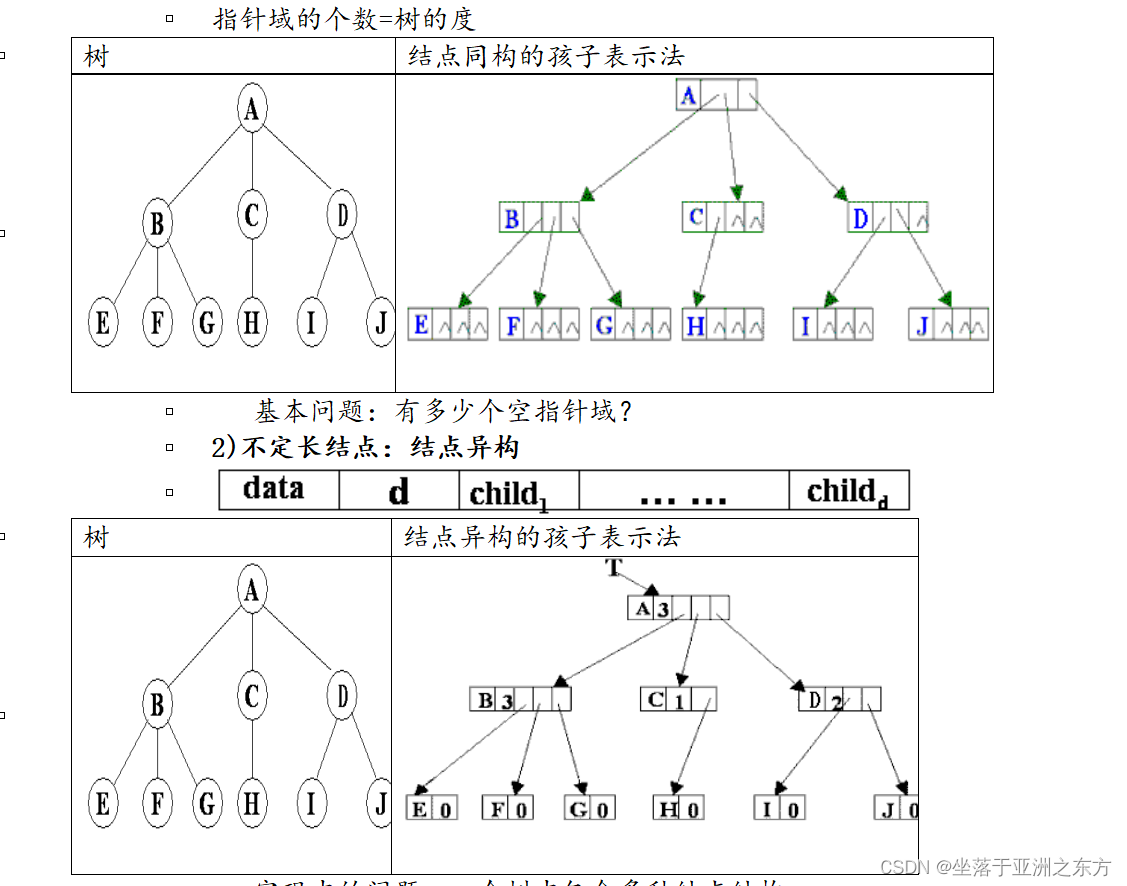
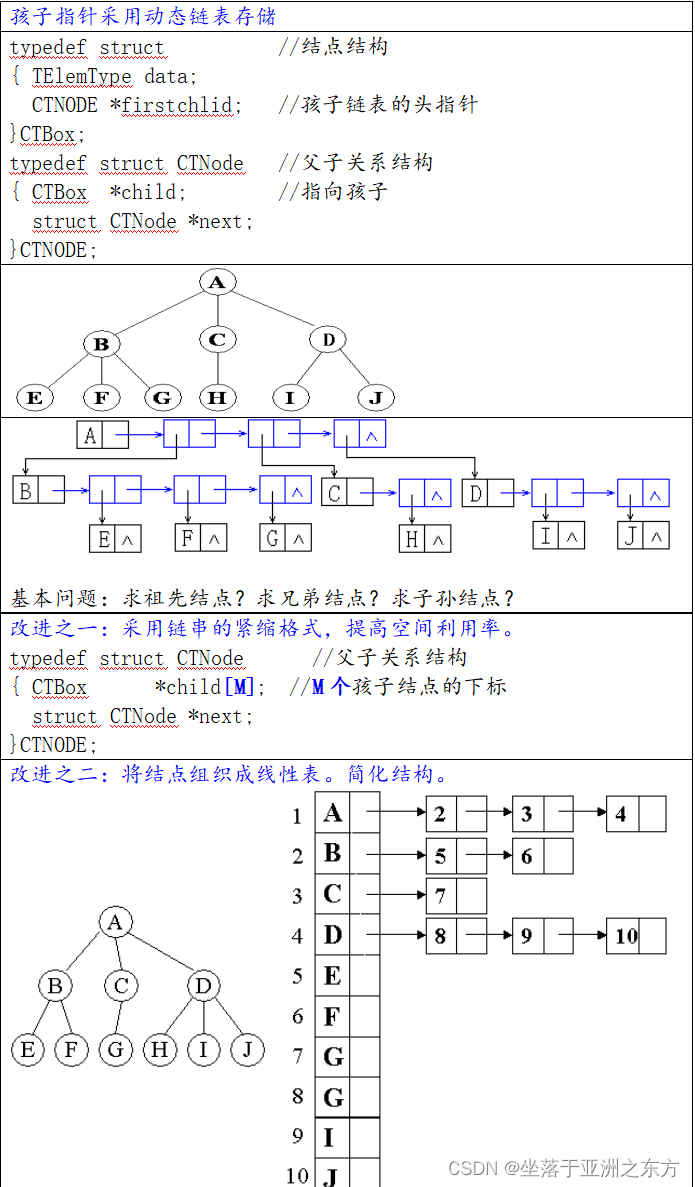
1、树结构与二叉树结构的一一对应关系
对树采用孩子兄弟法存储，得到目标二叉树。
源树与目标二叉树一一对应。
目标二叉树：根结点无右子树；
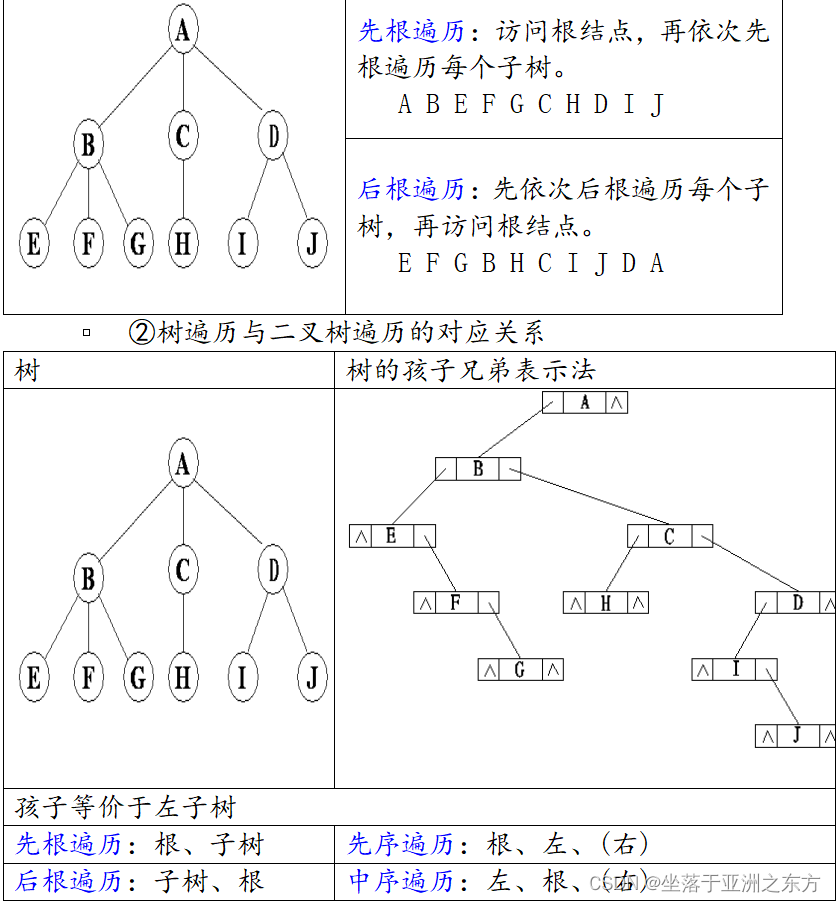
2、树操作与二叉树操作的一一对应关系
①基本操作：树的遍历

③应用问题：
计算树中每个结点的度？
已知树的存储结构为二叉链表结构，每个结点包含data、firstchild、nextsibling、degree四个域，要求将每个结点度数存入相应结点的degree域中。
// 遍历二叉树的套路
void Tree_Degree(CSNODE *root)
{ CSNODE *p;
if(rootNULL) return;
root->degree=0;
for(p=root->firstchild; p; p=p->nextsibling)
root->degree++;
Tree_Degree(root->firstchild);
Tree_Degree(root->nextsibling);
}
计算原树的叶子数？
// 遍历线性表的套路
int Tree_Leaf(CSNODE *root)
{ CSNODE *p;
int count=0;
if(rootNULL) return(0);
if(root->firstchildNULL) return(1);
for(p=root->firstchild; p; p=p->nextsibling)
count=count + Tree_Leaf§;
return(count);
}
计算原树的深度？
// 遍历线性表的套路
int Tree_Depth(CSNODE *root)
{ CSNODE *p;
int depth1,maxdepth=0;
if(rootNULL) return(0);
for(p=root->firstchild; p; p=p->nextsibling)
{ depth1=Tree_Depth§;
if(depth1>maxdepth) maxdepth=depth1;
}
return(maxdepth+1);
}

三、森林与树的转换

1、森林结构与二叉树结构的一一对应关系

孩子兄弟法：将所有树的根结点视为兄弟。

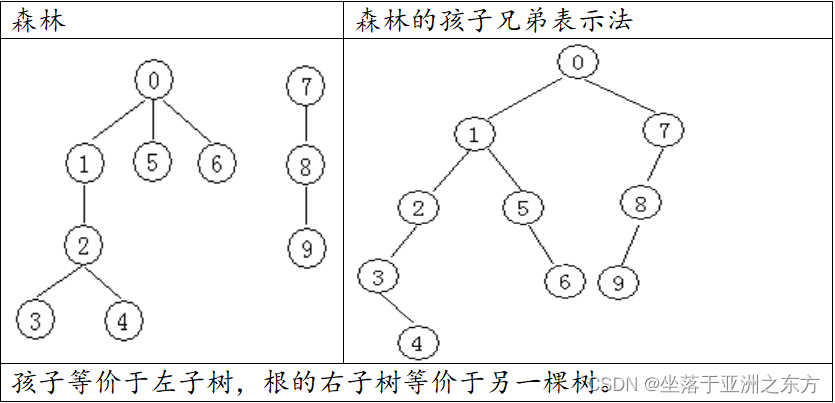
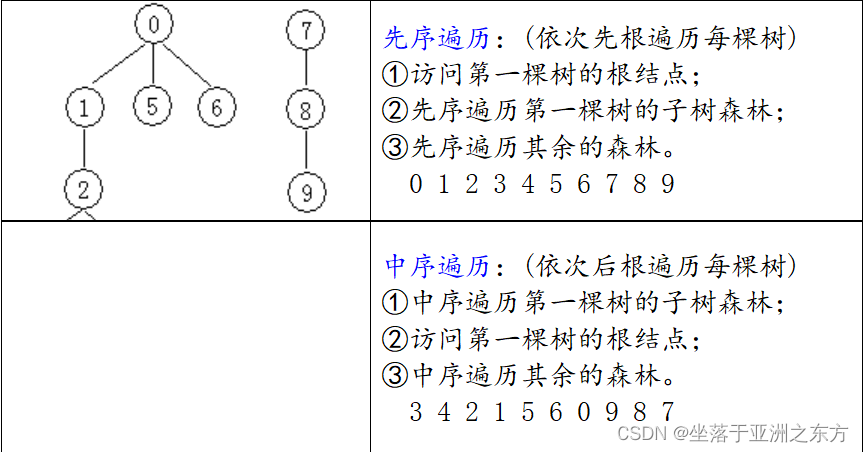
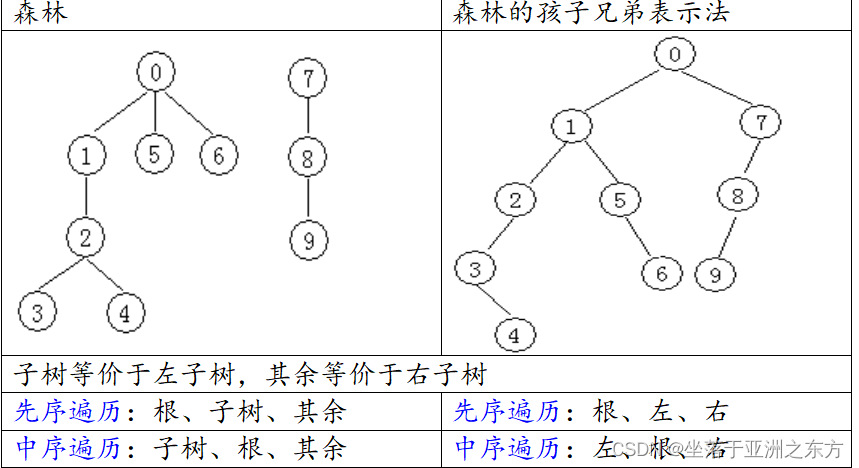
第六节 哈夫曼树及其应用

应用实例：文件压缩、解压。

一、术语

路径 ：连接结点之间的若干分支。
路径长度：路径的分支数。
结点路径长度：从根到该结点的路径长度。
树的路径长度：树中所有叶子结点的路径长度之和。
结点带权路径长度：结点路径长度与结点权的积。
树的带权路径长度：树中所有叶子结点的带权路径长度之和。
哈夫曼树(最优二叉树):
在叶子结点确定的前提下，带权路径长度最小的二叉树。

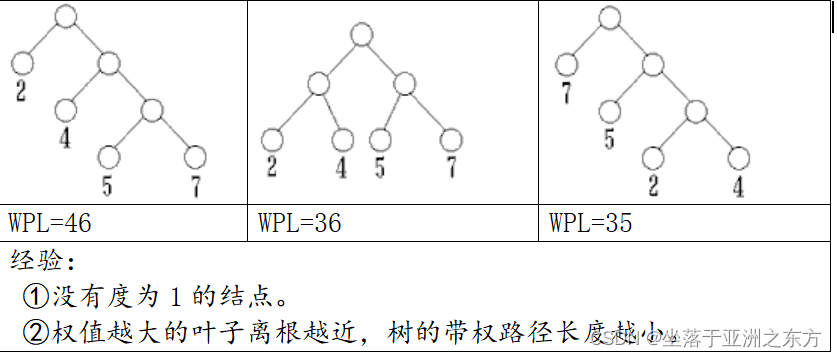
二、构造哈夫曼树的算法

已知：N个结点的权值为W1,……,WN，构造算法如下：
①根据(W1,……,WN)构成森林F=(T1,……,TN),每棵二叉树Ti有且只有一个根结点，权为Wi，左右子树为空；
②在F中选取二棵根的权值最小的树Ti、Tj，权为Wi、Wj，作为左右子树合成一棵新树Tk，Tk的根的权Wk=Wi+Wj；
③在F中删除Ti、Tj，加入Tk；
④重复②③，循环N-1次，F中只剩一棵树,即为哈夫曼树。

示例：0.4, 0.2, 0.1, 0.5
示例：0.22, 0.3, 0.4, 0.28

三、哈夫曼编码

1、信息编码的目标
源文件 =》 目标文件
编码目标： 目标文件长度尽可能短。
2、编码方法
统计编码原理：①基于概率分布特性；②编码长度不固定。
频率高的符号用较少的位。
问题1：
A的编码可以为"1"吗？B的编码可以为"11"吗？
前缀编码：任何符号的编码都不是另一符号编码的前缀。
统计编码必须是前缀编码！
问题2：编码的效率？
设 S1, S2, … , Sn是被编码的一组符号,
P1, P2, … , Pn是各自出现的概率,
L1, L2, … , Ln是码长，
则平均码长：见下

3、哈夫曼树中的哈夫曼编码

哈夫曼树的意义：
叶子：待编码的符号；
权值：待编码的符号的出现频率
叶子的路径：符号的哈夫曼编码
记：左分支=0，右分支=1。
哈夫曼编码的性质：
①前缀编码：各个叶子的路径决不会相互包含。
　 ②高效编码：树的带权路径长度=平均码长

4、压缩/解压软件的思路

设压缩单位为字节，
压缩模块的设计思路：
①统计源文件：0,1,……,255的出现次数=》“频率表”；
②根据“频率表”构造哈夫曼树；
③读取各字符的哈夫曼编码；
④将“频率表”写入压缩文件头；（文件头的格式设计？）
⑤翻译源文件，写入压缩文件。
解压模块的设计思路：
①读压缩文件头，得到“频率表”；
②根据“频率表”重构哈夫曼树；
③读压缩文件中的"0/1"串，从根搜索至叶子，将叶子对应的字符写入“解压文件”；
④重复③，直至译完压缩文件。
四、哈夫曼算法：建树、计算编码
存储结构：顺序？链式？
若结点数确定：采用静态链表。
若结点数不定：采用动态链表。
#define N 4 /* 需编码的字符数 /
#define M 7 / 哈夫曼树的结点数=2N-1 */
typedef struct //每个字符及相应权值
{ char ch;
float weight;
}Char_Weight;

typedef struct
{ char ch;
float weight;
int parent,lchild,rchild; //父结点，左、右孩子
}HuffNode;

typedef struct //每个字符的编码结构
{ int start;
int bits[N];
}HuffCode;

main()
{ Char_Weight W[N];
HuffNode HT[M]; HuffCode HC[N];
ReadWeight(W); // 读入权值
Huffman_Create(HT,W); //建树HT[M]
Huffman_Coding(HT,HC); //读编码HC[N]
}

void Huffman_Create(HuffNode HT[],Char_Weight W[])
{ for(i=0;i<N;i++) // 初始化N个树的森林
{ HT[i].ch= W[i].ch; // 为将来译码作准备
HT[i].parent=HT[i].lchild=HT[i].rchild=-1;
HT[i].weight=W[i].weight;
}
for(i=N;i<M;i++) // 合并树
{ select(HT,i-1,&n1,&n2); // n1最小，n2次小
// 可采用优先队列实现
HT[n1].parent=HT[n2].parent=i;
HT[i].parent=-1; HT[i].lchild=n1; HT[i].rchild=n2;
HT[i].weight=HT[n1].weight+HT[n2].weight;
}
}
示例：a:0.4, b:0.2, c:0.1, d:0.5

void HuffmanCoding(HuffNode HT[], HuffCode HC[])
{ int i,j, p, parent;
for(i=0; i<N; i++)
{ p=i; parent=HT[p].parent;
// 只有根结点的parent==-1
for(j=N-1; parent!=-1; j–)
{ if(HT[parent].lchild==p)
HT[i].bits[j]=0; //左子树为0
else HT[i].bits[j]=1; //右子树为1
p=parent; parent=HT[parent].parent;
}
HC[i].start=j+1;
}
}

五、哈夫曼算法：译码（密文=》明文）

void HuffmanDeCoding(HuffNode HT[],char source[],char dest[])
{ int i, p=M-1, k=0; // p为根结点下标，k是明文中字符数
for(i=0; source[i]; i++)
{ if(source[i]‘0’) p=HT[p].lchild;
else p=HT[p].rchild;
if(HT[p].lchild-1 && HT[p].lchild==-1) // 遇到叶子
{ dest[k++]=HT[p].ch; p=M-1; } // 翻译字符，从头再来
}
dest[k]=‘\0’;
}
附：哈夫曼树的在编程中的一个应用：
根据数据情况，改善条件判断的执行效率
if(x<60) grade=“不及格”; 0.05
else if(x<70) grade=“及格”; 0.15
else if(x<80) grade=“中等”; 0.40
else if(x<90) grade=“良好”; 0.30
else grade=“优秀”; 0.10

if(x<80)
if(x<70)
if(x<60) grade=“不及格”; 0.05
else grade=“及格”; 0.15
else grade=“中等”; 0.40
else
if(x<90) grade=“良好”; 0.30
else grade=“优秀”; 0.10