【MATLAB第48期】基于MATLAB的REMR-LSTM多次循环递归拓展理论的长短期记忆网络LSTM回归预测模型,PCA预处理降维
在本文中,将展示一个使用多次循环递归拓展(REMR)理论来改进LSTM回归预测问题。
通过多次循环,优化训练集和测试集输入权重,从而更新输入数据, 其次通过PCA主成分分析降维,控制特征数量。从而优化输入变量,改善训练模型,优化预测结果。
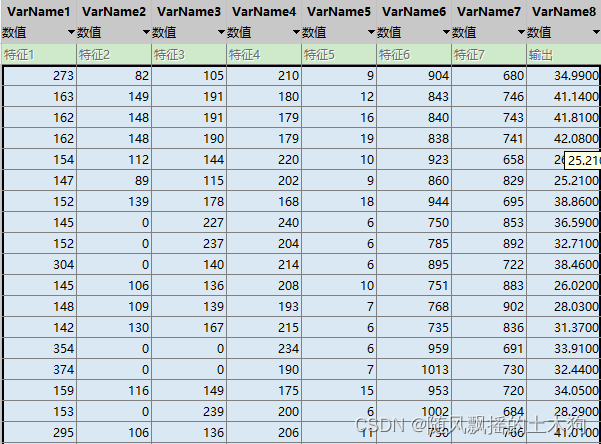
一、数据情况
103*8 前七列输入,最后一列输出
前80为训练集,后23为测试集。
%% 导入数据
res = xlsread('数据集.xlsx');
%% 划分训练集和测试集
temp =1:size(res,1);
P_train = res(temp(1: 80), 1: 7)';
T_train = res(temp(1: 80), 8)';
M = size(P_train, 2);
P_test = res(temp(81: end), 1: 7)';
T_test = res(temp(81: end), 8)';
N = size(P_test, 2);
%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
二、LSTM参数
layers = [
sequenceInputLayer(7) % 建立输入层
lstmLayer(4,'OutputMode','sequence') % LSTM层 , 'OutputMode', 'last'
reluLayer % Relu激活层
fullyConnectedLayer(1) % 全连接层
regressionLayer]; % 回归层
%% 参数设置
options = trainingOptions('adam', ... % Adam 梯度下降算法
'MiniBatchSize', 30, ... % 批大小
'MaxEpochs', 1200, ... % 最大迭代次数
'InitialLearnRate', 1e-2, ... % 初始学习率为
'LearnRateSchedule', 'piecewise', ... % 学习率下降
'LearnRateDropFactor', 0.5, ... % 学习率下降因子
'LearnRateDropPeriod', 800, ... % 经过 800 次训练后 学习率为 0.01 * 0.5
'Shuffle', 'every-epoch', ... % 每次训练打乱数据集
'Plots', 'none', ... % 画出曲线
'Verbose', 1);
三、LSTM运行结果
四、REMR-LSTM思路与运行结果
1.多次循环运行模型,设定循环次数。为了便于展示,循环次数设为5。
rounds=5;%循环次数5
2.建立训练模型 net
[network{j}]= LSTM_FUN(p_train,t_train);
3.初始化训练集与测试集输入变量权重
[Q_tr]= LSTM_w(LSTM,p_train'); %训练集模型输入权重
[Q_ts]= LSTM_w(LSTM,p_test'); %测试集模型输入权重
4.更新训练集与测试集输入变量
xtr=[ Q_tr tim1];
xts=[Q_ts tim2];
5.降维控制变量数量,得到最终变量
pca(xtr)
pca(xts)
6.带入新变量预测,得到评价结果
第三个子图可看出,训练集和测试集平均指标,在第五次循环结果最佳。
故选取第五次循环结果绘图。
与未优化前对比明显得到改善。
五、代码获取
后台私信回复“49期”可获取下载链接。