目录
前言:
上一篇文章中介绍了树的概念、深度优先遍历和广度优先遍历,这篇文章我们来学习一个特殊的树——二叉树。
什么是二叉树
二叉树是每个节点最多只能有两个子节点的树,如下图所示:
一个二叉树具有以下几个特质:
第i层的节点最有只有2^(i-1)个; 如果这颗二叉树的深度为k,那二叉树最多有2^k-1个节点; 在一个非空的二叉树中,若使用n0表示叶子节点的个数,n2是度为2的非叶子节点的个数,那么两者满足关系n0 = n2 + 1。
满二叉树
如果在一个二叉树中,除了叶子节点,其余的节点的每个度都是2,则说明该二叉树是一个满二叉树 ,
如下图所示:
满二叉树除了满足普通二叉树特质,还具有如下几个特质:
满二叉树的的第n层具有2^(n-1)个节点; 深度为k的满二叉树一定存在2^k-1个节点,叶子节点的个数为2^(k-1); 具有n个节点的满二叉树的深度为log_2^(n+1)。
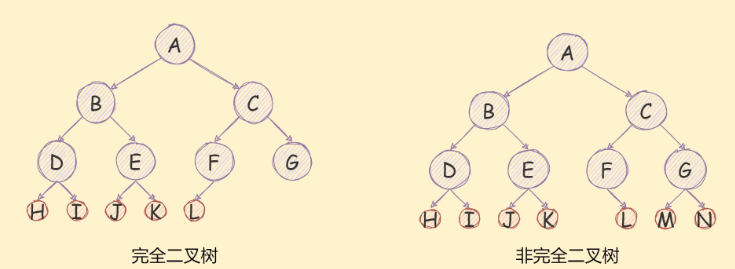
完全二叉树
如果一个二叉树去掉最后一次层是满二叉树,且最后一次的节点是依次从左到右分布 的,则这个二叉树是一个完全二叉树,
如下图所示:
二叉树的存储
存储二叉树的常见方式分为两种,一种是使用数组存储 ,另一种使用链表存储。
数组存储
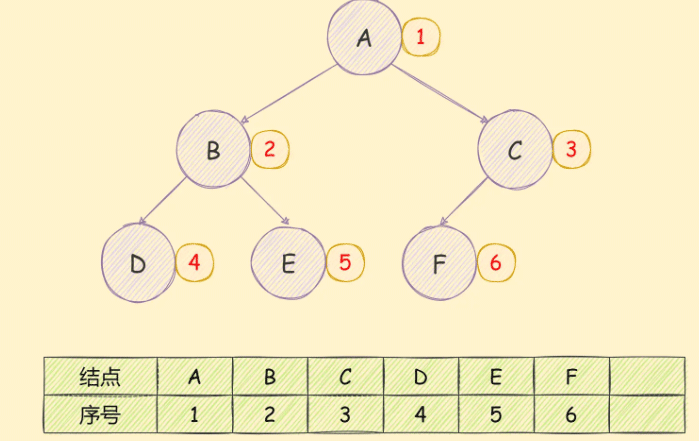
使用数组存储二叉树,如果遇到完全二叉树,存储顺序从上到下,从左到右,如下图所示:
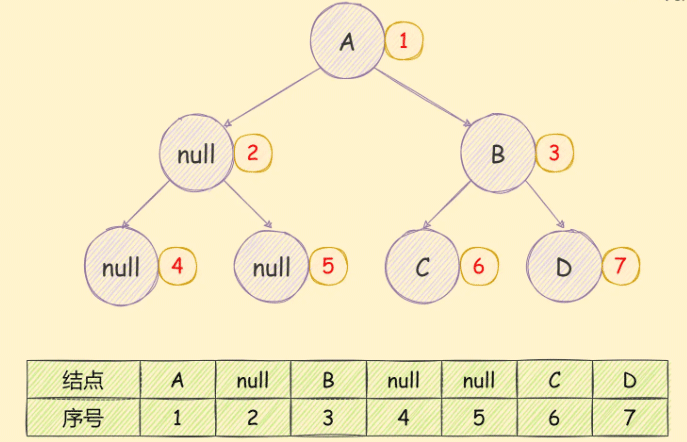
如果是一个非完全二叉树,如下图所示:
需要先将其转换为完全二叉树,然后在进行存储,如下图所示:
可以很明显的看到存储空间的浪费。
链表存储
使用链表存储通常将二叉树中的分为3个部分,如下图:
这三个部分依次是左子树的引用,该节点包含的数据,右子树的引用,存储方式如下图所示:
与二叉树相关的算法
以下算法中遍历用到的树如下 :
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// tree.js
const bt = {
val: 'A',
left: {
val: 'B',
left: { val: 'D', left: null, right: null },
right: { val: 'E', left: null, right: null },
},
right: {
val: 'C',
left: {
val: 'F',
left: { val: 'H', left: null, right: null },
right: { val: 'I', left: null, right: null },
},
right: { val: 'G', left: null, right: null },
},
}
module.exports = bt
深度优先遍历
二叉树的深度优先遍历与树的深度优先遍历思路一致,思路如下:
访问根节点; 访问根节点的left 访问根节点的right 重复执行第二三步 实现代码如下:
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
const bt = {
val: 'A',
left: {
val: 'B',
left: { val: 'D', left: null, right: null },
right: { val: 'E', left: null, right: null },
},
right: {
val: 'C',
left: {
val: 'F',
left: { val: 'H', left: null, right: null },
right: { val: 'I', left: null, right: null },
},
right: { val: 'G', left: null, right: null },
},
}
function dfs(root) {
if (!root) return
console.log(root.val)
root.left && dfs(root.left)
root.right && dfs(root.right)
}
dfs(bt)
/** 结果
A B D E C F H I G
*/
广度优先遍历
实现思路如下:
创建队列,把根节点入队 把对头出队并访问 把队头的left和right依次入队 重复执行2、3步,直到队列为空 实现代码如下:
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
function bfs(root) {
if (!root) return
const queue = [root]
while (queue.length) {
const node = queue.shift()
console.log(node.val)
node.left && queue.push(node.left)
node.right && queue.push(node.right)
}
}
bfs(bt)
/** 结果
A B C D E F G H I
*/
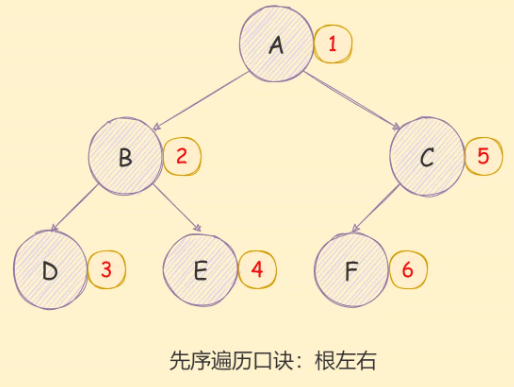
先序遍历
二叉树的先序遍历实现思想如下:
访问根节点; 对当前节点的左子树进行先序遍历; 对当前节点的右子树进行先序遍历; 如下图所示:
递归方式实现如下:
?
1
2
3
4
5
6
7
8
9
10
11
12
const bt = require('./tree')
function preorder(root) {
if (!root) return
console.log(root.val)
preorder(root.left)
preorder(root.right)
}
preorder(bt)
/** 结果
A B D E C F H I G
*/
迭代方式实现如下:
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 非递归版
function preorder(root) {
if (!root) return
// 定义一个栈,用于存储数据
const stack = [root]
while (stack.length) {
const node = stack.pop()
console.log(node.val)
/* 由于栈存在先入后出的特性,所以需要先入右子树才能保证先出左子树 */
node.right && stack.push(node.right)
node.left && stack.push(node.left)
}
}
preorder(bt)
/** 结果
A B D E C F H I G
*/
中序遍历
二叉树的中序遍历实现思想如下:
对当前节点的左子树进行中序遍历; 访问根节点; 对当前节点的右子树进行中序遍历; 如下图所示:
递归方式实现如下:
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
const bt = require('./tree')
// 递归版
function inorder(root) {
if (!root) return
inorder(root.left)
console.log(root.val)
inorder(root.right)
}
inorder(bt)
/** 结果
D B E A H F I C G
*/
迭代方式实现如下:
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 非递归版
function inorder(root) {
if (!root) return
const stack = []
// 定义一个指针
let p = root
// 如果栈中有数据或者p不是null,则继续遍历
while (stack.length || p) {
// 如果p存在则一致将p入栈并移动指针
while (p) {
// 将 p 入栈,并以移动指针
stack.push(p)
p = p.left
}
const node = stack.pop()
console.log(node.val)
p = node.right
}
}
inorder(bt)
/** 结果
D B E A H F I C G
*/
后序遍历
二叉树的后序遍历实现思想如下:
对当前节点的左子树进行后序遍历; 对当前节点的右子树进行后序遍历; 访问根节点; 如下图所示:
递归方式实现如下:
?
1
2
3
4
5
6
7
8
9
10
11
12
13
const bt = require('./tree')
// 递归版
function postorder(root) {
if (!root) return
postorder(root.left)
postorder(root.right)
console.log(root.val)
}
postorder(bt)
/** 结果
D E B H I F G C A
*/
迭代方式实现如下:
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 非递归版
function postorder(root) {
if (!root) return
const outputStack = []
const stack = [root]
while (stack.length) {
const node = stack.pop()
outputStack.push(node)
// 这里先入left需要保证left后出,在stack中后出,就是在outputStack栈中先出
node.left && stack.push(node.left)
node.right && stack.push(node.right)
}
while (outputStack.length) {
const node = outputStack.pop()
console.log(node.val)
}
}
postorder(bt)
/** 结果
D E B H I F G C A
*/