【计算机图形学】期末复习,选择题+判断题篇
题目来源于百度、B站、中国大学慕课网,适用于期末复习,内容仅供参考,祝大家考试顺利通过!!!
文章目录
- 【计算机图形学】期末复习,选择题+判断题篇
- 第一讲 计算机图形学概论
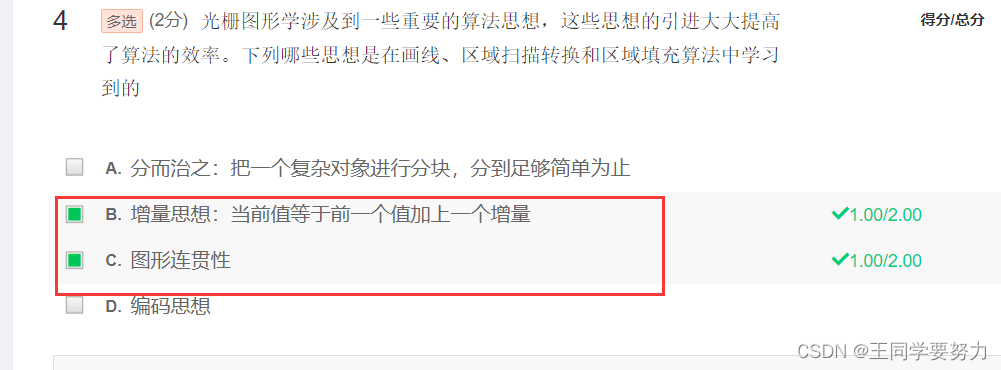
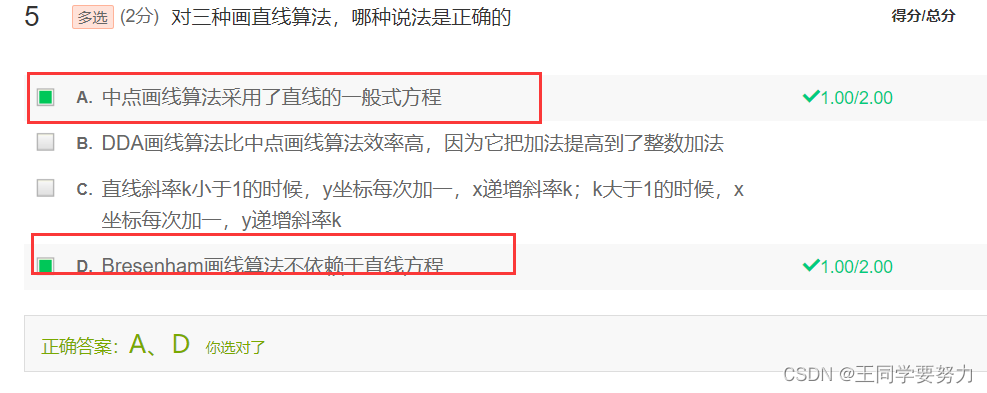
- 第二讲 光栅图形学算法(一)
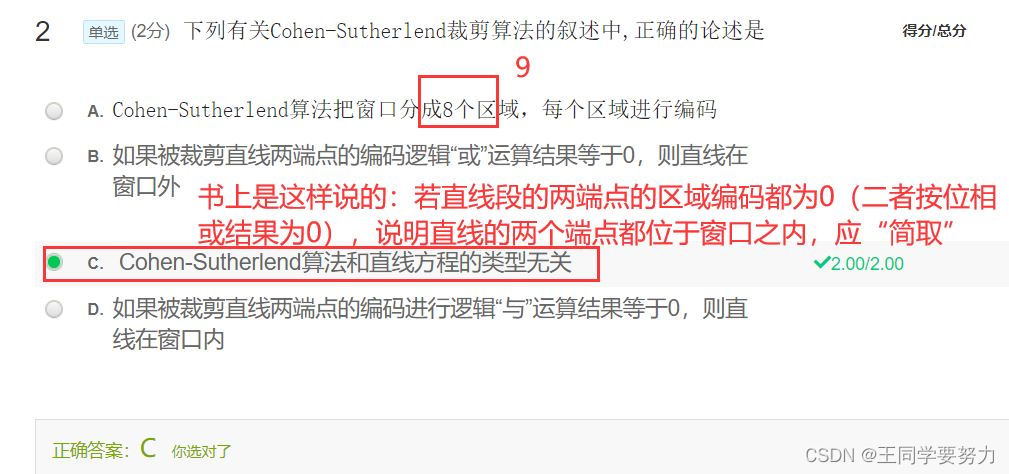
- 第三讲 裁剪算法(光栅图形学算法续)
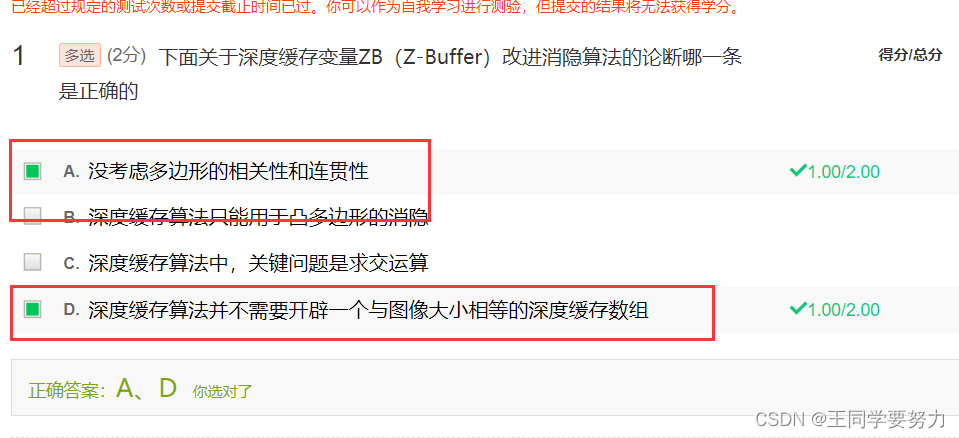
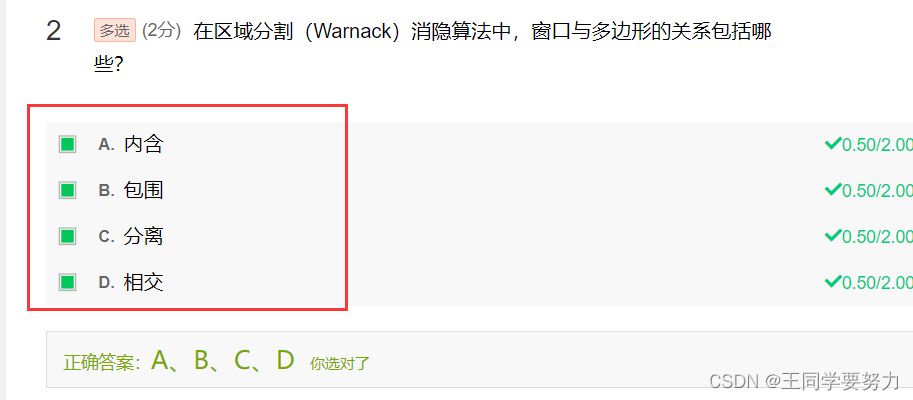
- 第四讲 消隐算法(光栅图形学算法续)
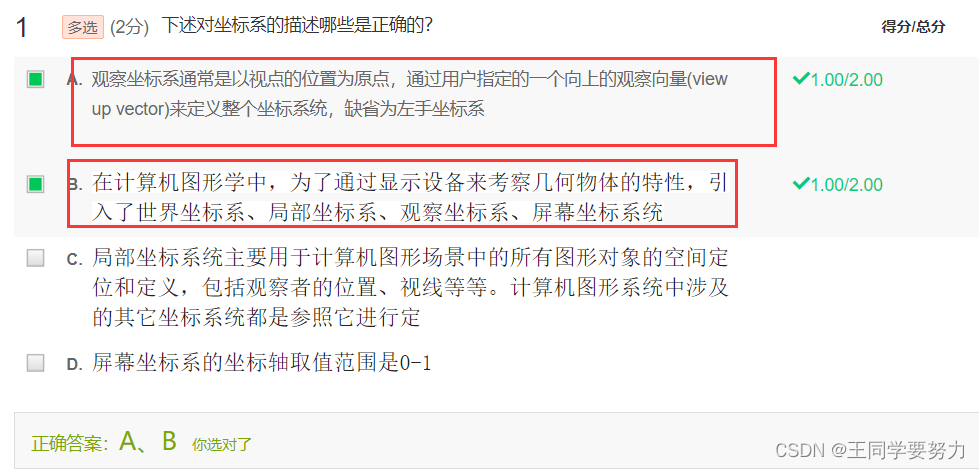
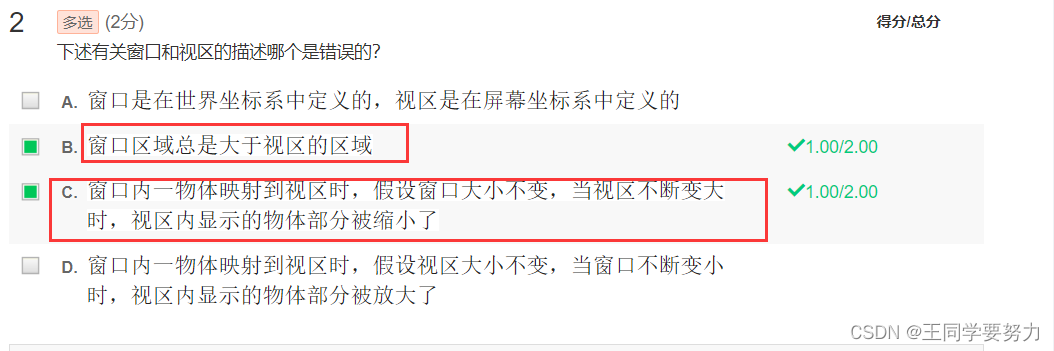
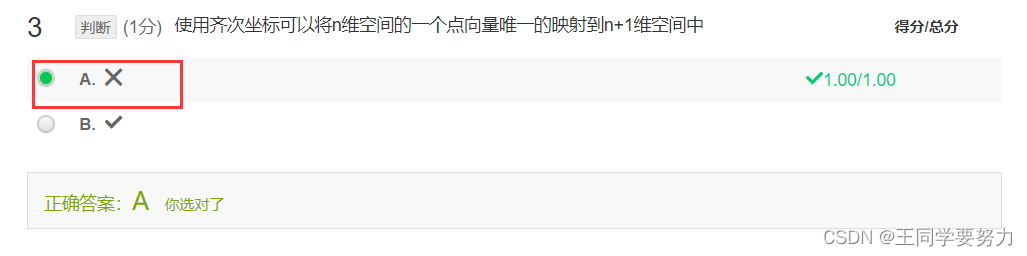
- 第五讲 二维图形变换
- 第六讲 三维图形变换
- 第七讲 曲线曲面(一)
- 第八讲 曲线曲面(二)
- 第九讲 真实感图形学
第一讲 计算机图形学概论
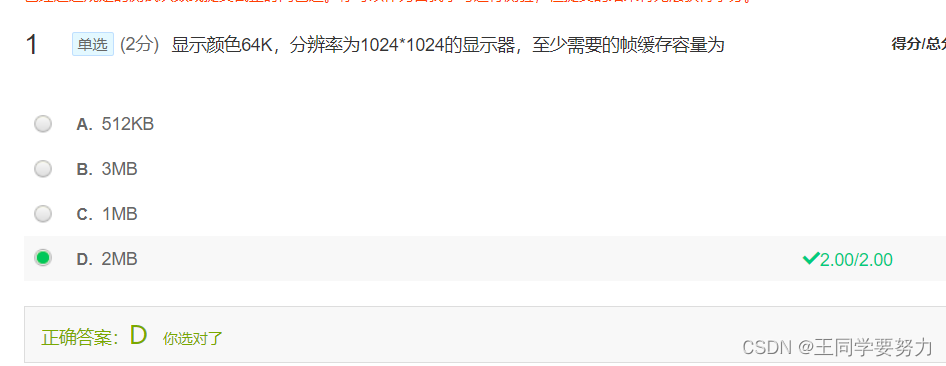
每个像素需要占用 16 位,即 2 个字节,因此该显示器所需的帧缓存器容量为:1024 × 1024 × 2 = 2,097,152 B = 2 MB,因此,该显示器至少需要 2 MB 的帧缓存器容量。
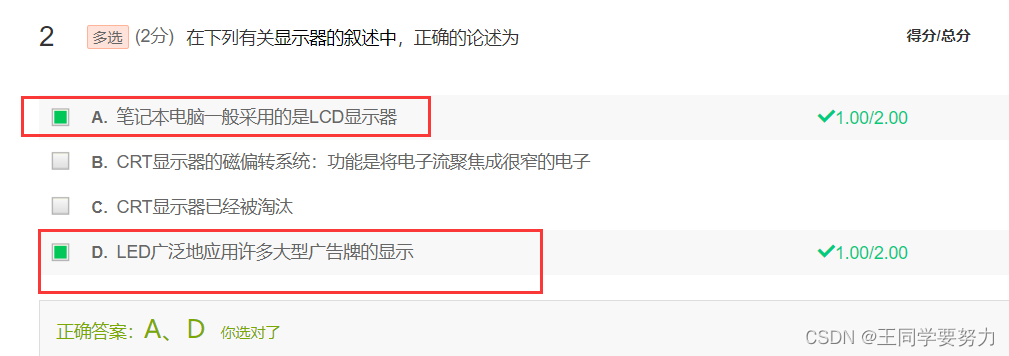
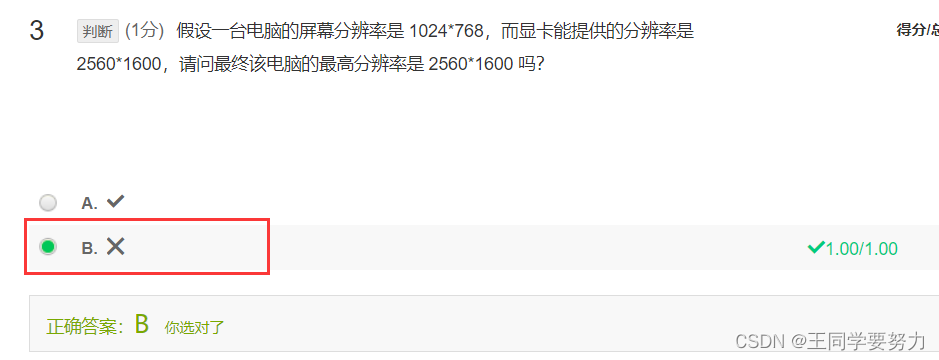
该电脑的最高分辨率仍然是1024*768,因为显示器的分辨率是固定的,不能超过其物理上的像素点数量。
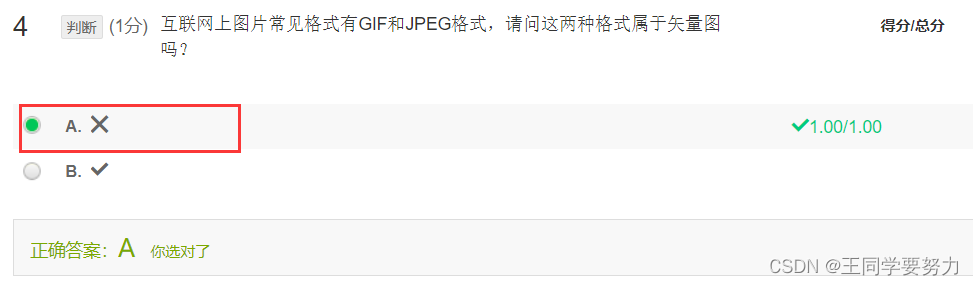
GIF和JPEG格式都不属于矢量图格式。它们属于光栅图(也称为位图)格式,即用像素来描述图像的格式。 矢量图使用数学公式来描述图像,相对而言具有无限的可伸缩性而不会有失真问题,但是,它们不能很好地呈现复杂或实时动态图像,因此光栅图格式在这些情况下更为常见。
第二讲 光栅图形学算法(一)
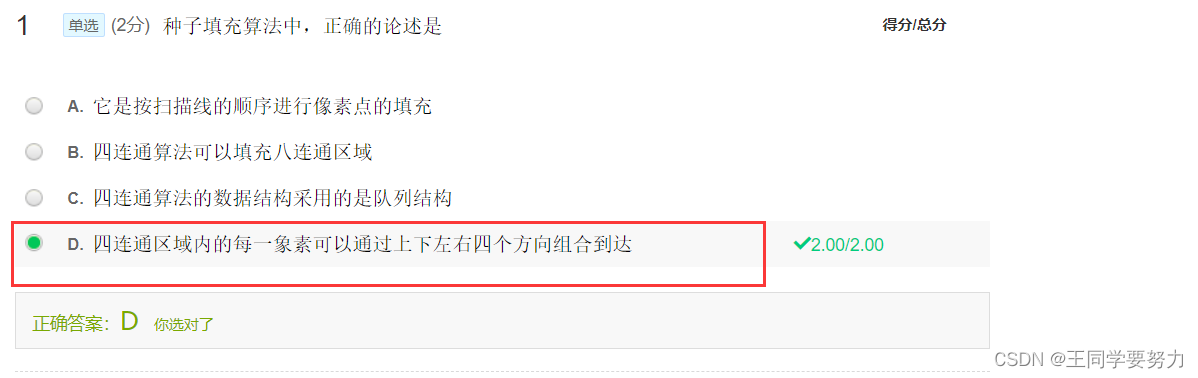
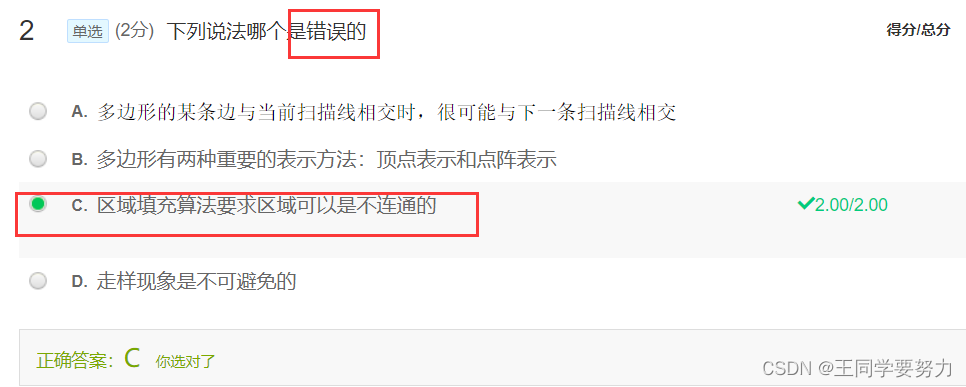
区域填充算法要求区域必须是连通的。这是因为区域填充算法是一种递归算法,它通过填充相邻像素的方式来扩展填充区域。如果区域不是连通的,那么填充算法无法继续递归扩展填充区域。
第三讲 裁剪算法(光栅图形学算法续)

第四讲 消隐算法(光栅图形学算法续)
第五讲 二维图形变换
第六讲 三维图形变换
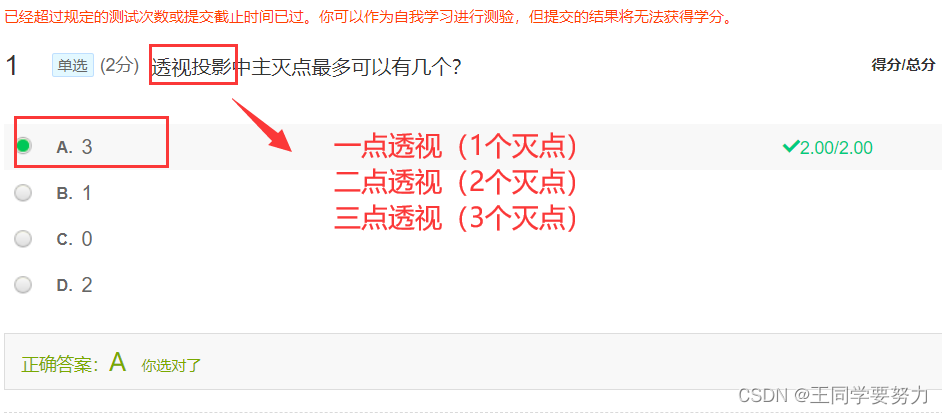
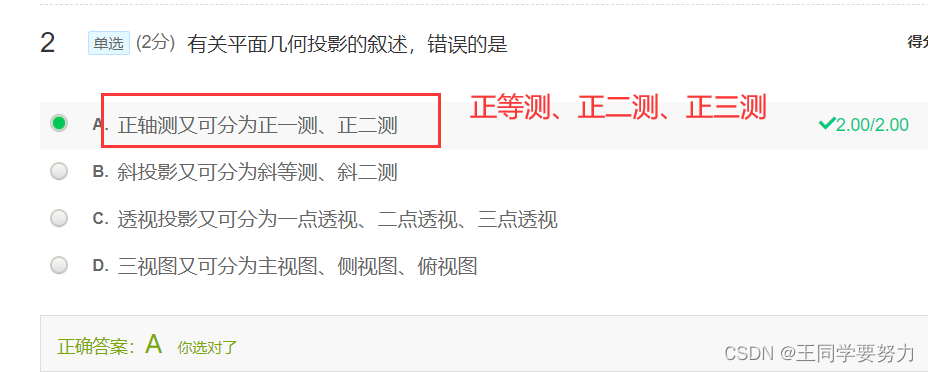
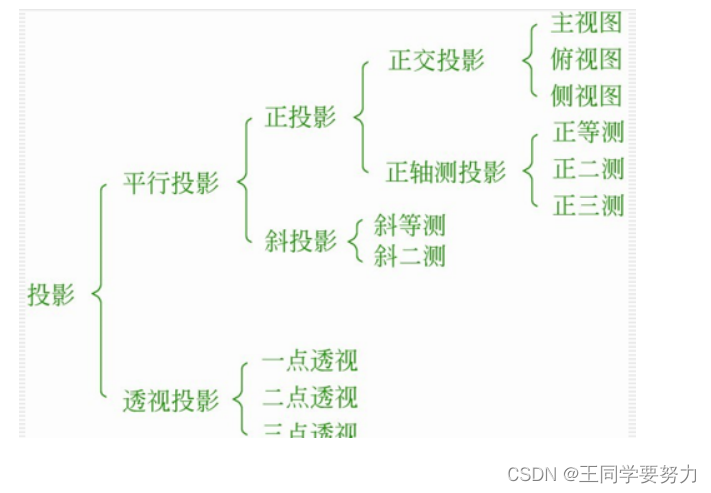
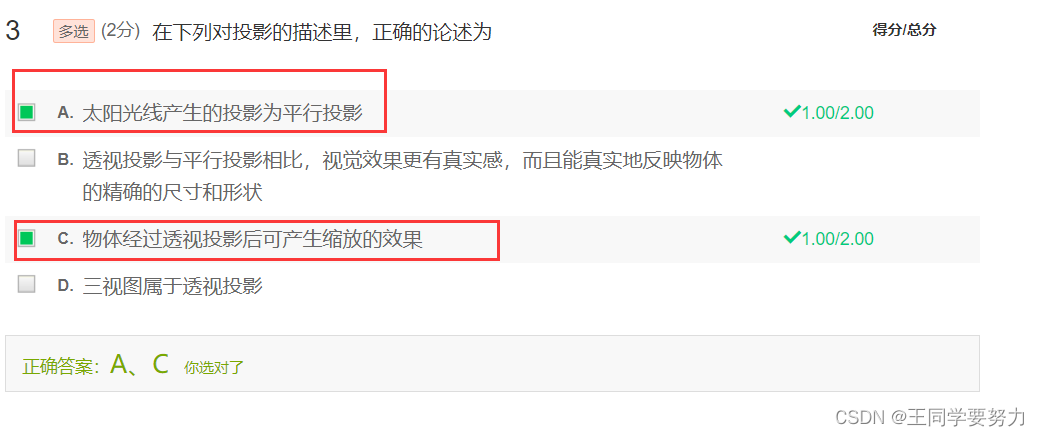
第七讲 曲线曲面(一)
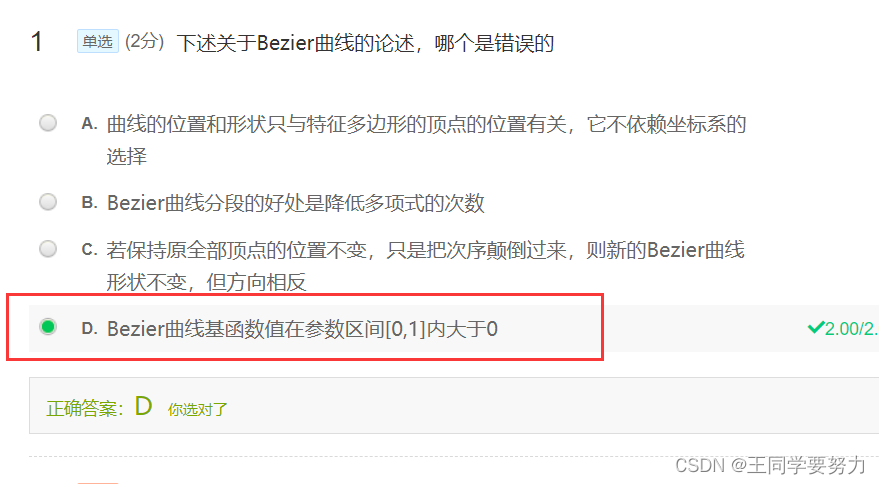
关于Bezier曲线基函数在参数区间[0,1]内大于0的问题,这个说法是有误的。事实上,Bezier曲线的基函数可以取负值。
Bezier曲线是通过参数化多个控制点之间的插值来构建的,曲线上的任一点都可以通过控制点之间的插值来计算得出。控制点之间的插值使用了一组基函数,这些基函数通常是Bezier基函数,它们是通过组合泊松分布的多项式函数生成的,具体的表达式是一个二项式系数与多项式函数相乘之和。Yuri Gurevich和George Shpenkov在1985年在一篇论文中证明了这样一条定理:对任意正整数n和任意t∈[0,1],Bezier基函数B(i,n,t)的符号都不是一组正值或非负值。
因此,我们不能说Bezier曲线的基函数值在参数区间[0,1]内大于0,而只能说Bezier曲线的基函数存在符号变化,或者说存在正负性,不能做出简单的单调性或符号性论断。这很重要,因为关于Bezier曲线的许多理论和基于Bezier曲线的计算都基于其符号性质。
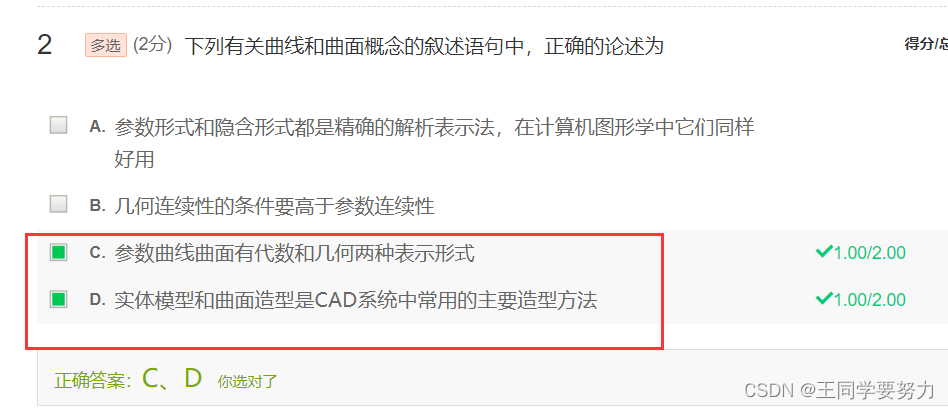
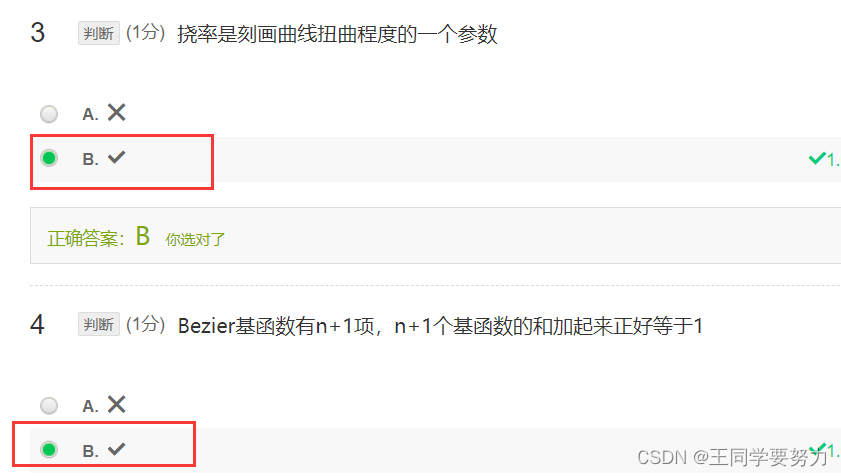
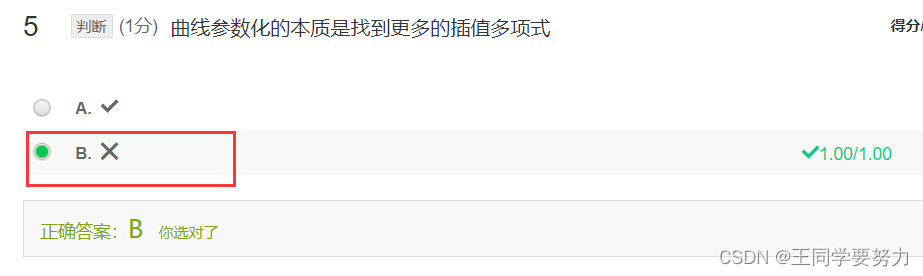
解答:曲线参数化并不是直接找到曲线上的插值多项式。插值多项式是一种通过已知的数据点来推导出曲线函数的方法,而曲线参数化则是通过选取合适的参数来描述曲线的几何形状。曲线参数化的本质是将曲线上的点与参数建立映射关系,将曲线上的点表示成参数化函数的形式。这个参数化函数的值域通常是一个参数空间,例如参数t的区间,这个函数可以是二维向量空间甚至更高维度的空间。曲线上的每个点都对应于参数空间中的一个点,这种映射关系就是曲线的参数化。
通过曲线的参数化,我们可以更方便地描述曲线的特性,比如曲线的长度、曲率、曲线的切线以及法线方向等。例如,在计算机图形学中,曲线参数化是在曲线渲染、曲线拟合等方面的重要基础工具,使用曲线参数化可以方便地计算曲线上的各种属性,以便更好地呈现和控制曲线的行为。因此曲线参数化和插值多项式是不同的概念,虽然它们在某些应用领域(如曲线拟合)中有重叠的应用。
第八讲 曲线曲面(二)
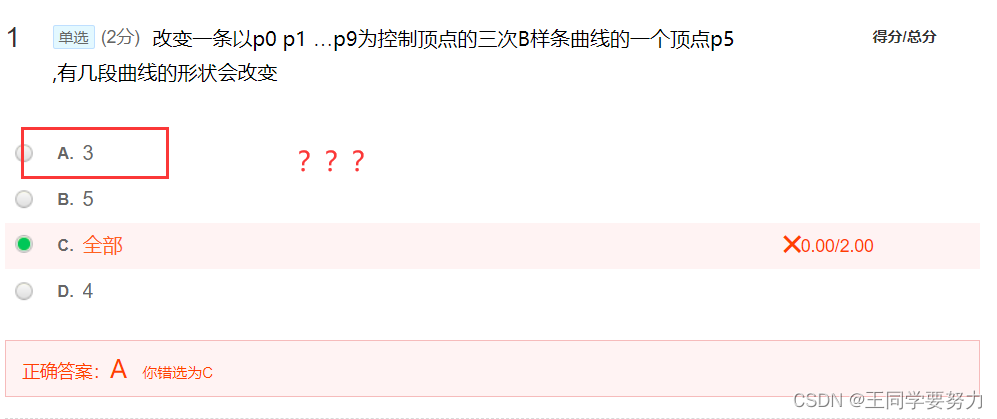
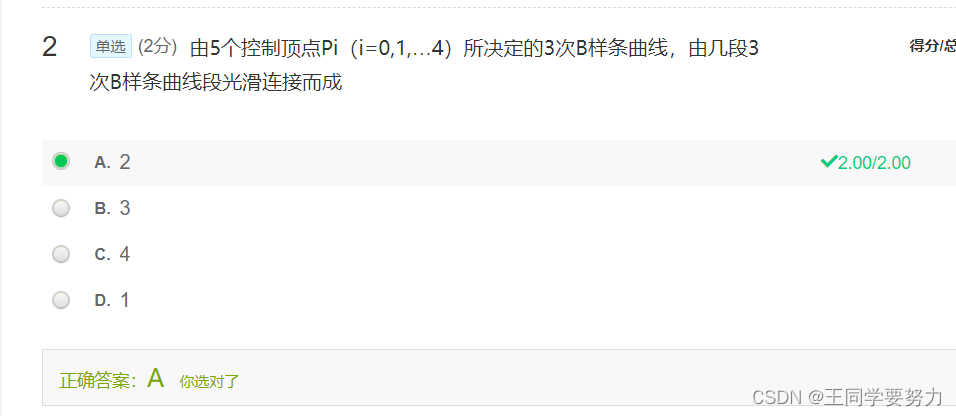

第九讲 真实感图形学
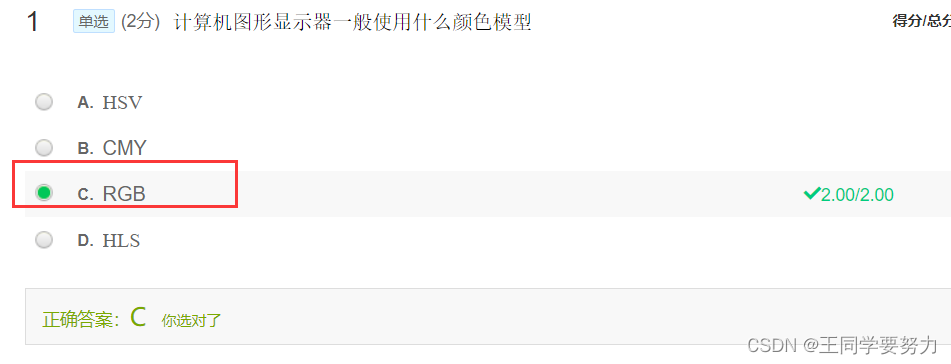
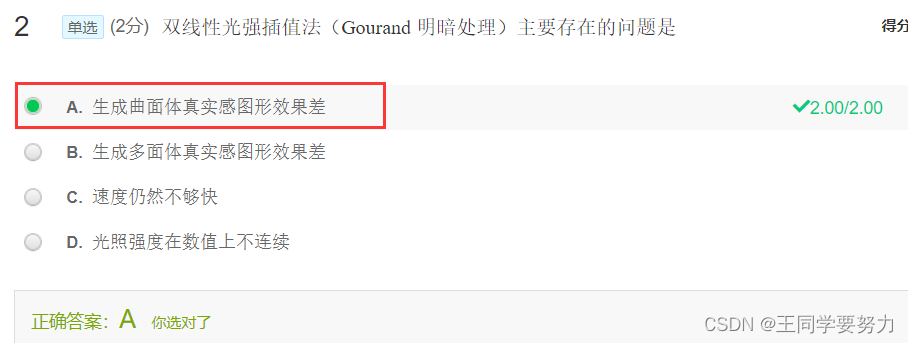
最后,祝大家考试顺利👏👏👏