一、背景
JavaScript中存在精度缺失问题

为什么?
主要是由于浮点数的表示方式以及计算机的二进制运算原理导致的
JavaScript使用IEEE 754标准定义了浮点数的表示和计算规则。在这种表示方式中,浮点数由符号位、指数位和尾数位组成。尾数位的长度是固定的,一般为53位。但是,无论是整数还是小数,都需要通过二进制表示来存储,而不是十进制。这就导致了某些十进制小数在二进制表示中是无限循环的,因此无法完全精确地表示。
例如,0.1这个十进制小数在二进制中是无限循环的,无法准确表示。因此,在进行计算时,可能会出现舍入误差。多次的舍入误差累积起来就会导致精度缺失问题。
此外,JavaScript中的数值计算是通过二进制进行的,而不是十进制。由于二进制和十进制之间的转换存在精度限制,导致一些十进制的小数无法完全准确地转换为二进制,进而引发精度缺失。
为了解决这个问题,可以使用一些特殊的库或技术,如BigNumber.js或Decimal.js,来处理大数和小数运算,以提高精度和准确性。另外,在涉及到金额计算等需要高精度的场景中,可以将数值转换为整数进行计算,然后再进行必要的除法或格式化操作,以减少精度缺失的影响。
二、Decimal
1、decimal介绍
decimal.js文档地址:decimal.js
decimal.js是使用二进制来计算的,所以可以更好地实现格化式数学运算,对数字进行高精度处理;使用decimal类型处理数据可以保证数据计算更为精确,还可以节省储存空间。
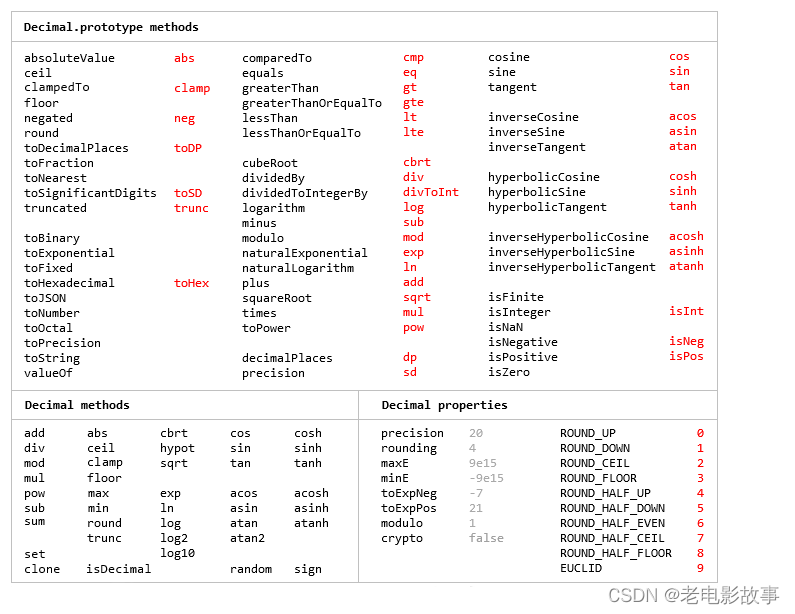
这里的精度是根据有效数字而不是小数位来指定的,并且所有计算都四舍五入到精度(类似于 Python 的十进制模块),而不仅仅是涉及除法的计算
2、使用方法
安装
npm install --save decimal.js
页面引入
import { Decimal } from 'decimal.js'
加减乘除
const a = 2.998;
const b = 8.035;
// 加法
let c = new Decimal(a).add(new Decimal(b))
// 减法
let d = new Decimal(a).sub(new Decimal(b))
// 乘法
let e = new Decimal(a).mul(new Decimal(b))
// 除法
let f = new Decimal(a).div(new Decimal(b))
const a = 0.00002
const b = 0.00001
this.aaa = Decimal(a).add(Decimal(b))
console.log(this.aaa)
打印后

3、decimal.js函数封装
// 引入 Decimal.js 库
const Decimal = require('decimal.js');
// 封装加法函数
function add(num1, num2) {
const decimal1 = new Decimal(num1);
const decimal2 = new Decimal(num2);
return decimal1.plus(decimal2).toString();
}
// 封装减法函数
function subtract(num1, num2) {
const decimal1 = new Decimal(num1);
const decimal2 = new Decimal(num2);
return decimal1.minus(decimal2).toString();
}
// 封装乘法函数
function multiply(num1, num2) {
const decimal1 = new Decimal(num1);
const decimal2 = new Decimal(num2);
return decimal1.times(decimal2).toString();
}
// 封装除法函数
function divide(num1, num2) {
const decimal1 = new Decimal(num1);
const decimal2 = new Decimal(num2);
return decimal1.dividedBy(decimal2).toString();
}
// 使用示例
console.log(add('0.1', '0.2')); // 输出:0.3
console.log(subtract('1.5', '0.8')); // 输出:0.7
console.log(multiply('2.5', '1.2')); // 输出:3
console.log(divide('6', '2')); // 输出:3
三、Bignumber
1、bignumber介绍
bignumber.js文档地址:bignumber.js

2、使用方法
npm install bignumber.js
import BigNumber from "bignumber.js"
- 加法 .plus(n [, base]) ⇒ BigNumber
- 减法 .minus(n [, base]) ⇒ BigNumber
- 乘法 .times(n [, base]) ⇒ BigNumber
- 除法 .div(n [, base]) ⇒ BigNumber
- 取模/取余: .mod(n [, base])
- 指数运算: .pow(n [, m]) ⇒ BigNumber
- 开平方:.sqrt() ⇒ BigNumber
- 比较大小: .comparedTo(n [, base]) ⇒ number
- 精度调整 .dp([dp [, rm]]) ⇒ BigNumber|number
- 取整:.integerValue([rm]) ⇒ BigNumber
- 有效数字 .sd([d [, rm]]) ⇒ BigNumber|number
- 保留小数位数 .toFixed([dp [, rm]]) ⇒ string
let x = 6.2000, y = 3.10, z = 9;
console.log('9999--plus---',BigNumber(0.7).plus(x).plus(y).toString()); // 10
console.log('9999--minus---',BigNumber(x).minus(2).toString()); // 4.2
console.log('9999--times---',BigNumber(x).times(10).toString()); // 62
console.log('9999--div---',BigNumber(x).div(y).toString()); // 2
console.log('9999--mod---',BigNumber(x).mod(y).toString()); // 0
console.log('9999--pow---',BigNumber(x).pow(-2).toString()); // 0.0260145681581685744
console.log('9999--sqrt---',BigNumber(z).sqrt().toString()); // 3
console.log('9999--toFixed---',BigNumber(x).toFixed(1).toString()); // 6.2
console.log('9999--integerValue---',BigNumber(x).integerValue(1).toString()); // 6
console.log('9999--sd---',BigNumber(x).sd().toString()); // 2
console.log('9999--comparedTo---',BigNumber(x).comparedTo(y).toString()); //1, 1为大于,-1为小于,0为等于