神奇的斐波那契数列和青蛙跳台阶问题
- 一、神奇的斐波那契数列
- 1.1、题目描述
- 1.2、递归算法
- 1.3、迭代法
- 1.4、小结
- 二、青蛙跳台阶问题
- 2.1、题目描述
- 2.2、思路
- 2.3、动态规划法
- 2.4、小结
- 三、矩阵中的路径
- 3.1、题目描述
- 3.2、思路
- 3.3、代码实现
- 3.4、小结
- 总结
一、神奇的斐波那契数列
1.1、题目描述
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:1
示例 2:
输入:n = 5
输出:5
来源:力扣(LeetCode)
1.2、递归算法
递归算法实现斐波那契数列。
int Fibonacci(int n)
{
if (n <= 0)
return 0;
if (n == 1 || n == 2)
return 1;
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
如果是leetcode上测试,会提示超时。
斐波那契数列的通项公式:
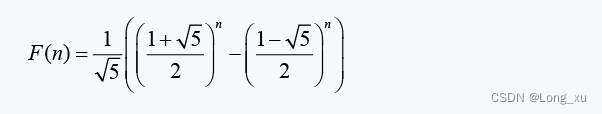
这里可以看到,时间复杂度属于爆炸增量函数。
1.3、迭代法
只需要第n个斐波那契数,中间结果只是为了下一次使用,不需要保存。所以,可以采用迭代法。
class Solution {
public:
int fib(int n) {
if(n<=0)
return 0;
else if(n==1 || n==2)
return 1;
int f1=1;
int f2=1;
for(int i=3;i<=n;i++)
{
int tmp=f1+f2;
f1=f2;
f2=tmp%1000000007;
}
return f2;
}
};
leetcode上测试是,答案需要取模 1e9+7(1000000007)。
时间复杂度:O(n)。
空间复杂度:O(1)。
1.4、小结
除了迭代法将时间复杂度降到了O(n),还有一种数学公式方式,使用矩阵快速幂将时间复杂度降到O(log n)。
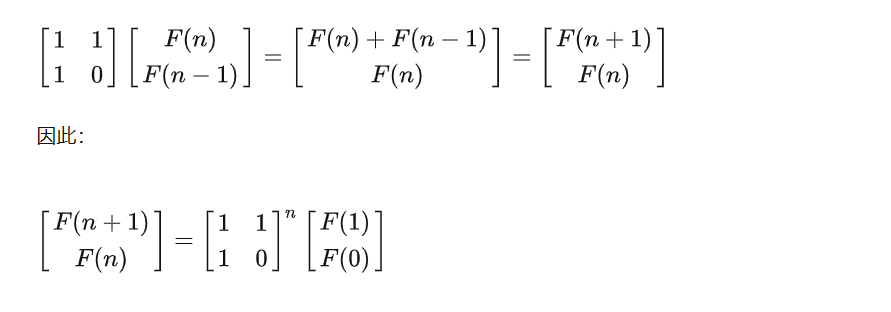
二、青蛙跳台阶问题
2.1、题目描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
要求:答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:2
示例 2:
输入:n = 7
输出:21
示例 3:
输入:n = 0
输出:1
来源:力扣(LeetCode)
2.2、思路
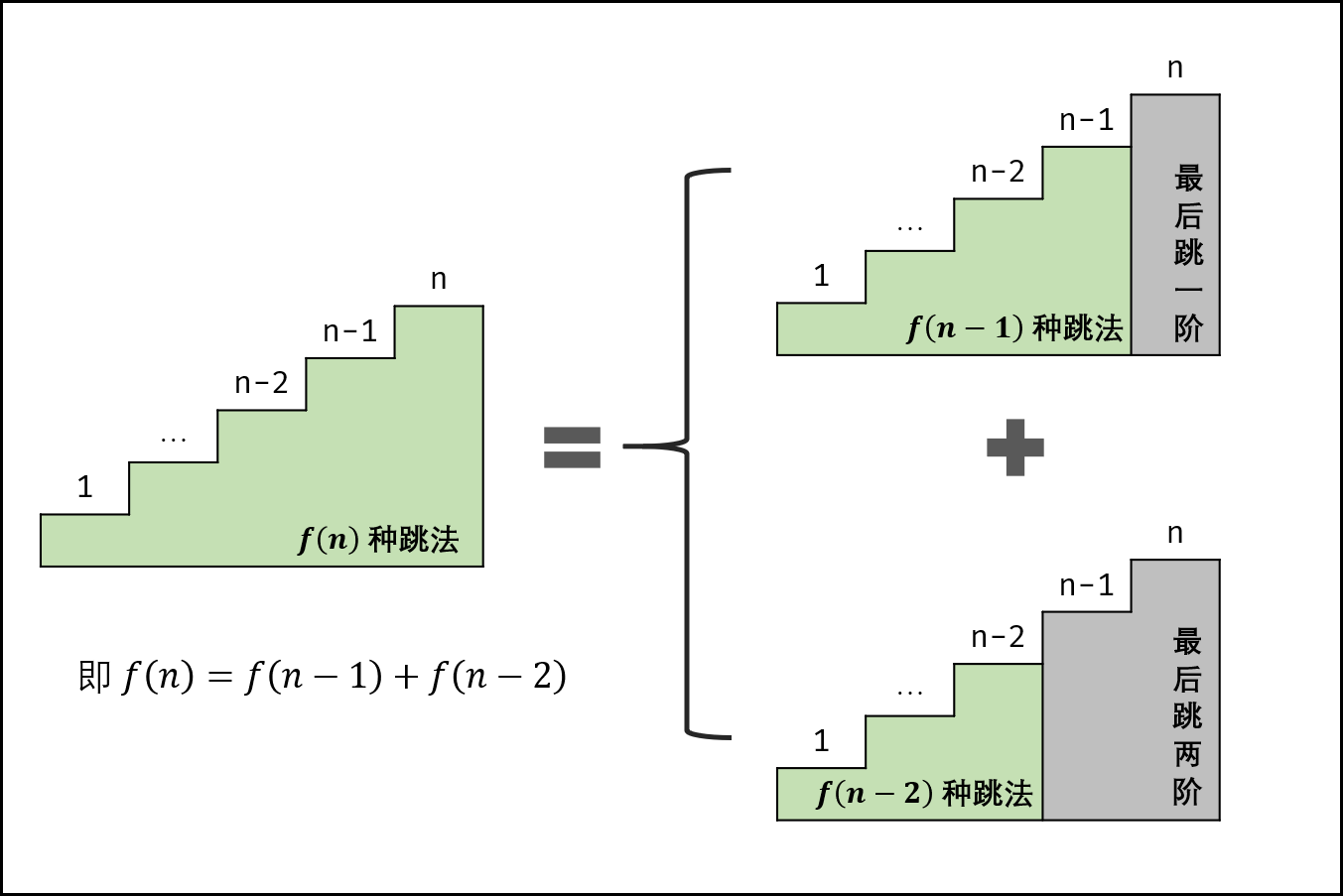
这个和斐波那契数列(Fibonacci sequence)非常相似。像这种求多少种可能性的题目一般都有递推性质,即f(n)和f(n-1)…f(1)之间是有联系的;即 f(n)=f(n-1)+f(n-2)。可转化为 求斐波那契数列第n项的值 ,唯一的不同在于起始数字不同。
青蛙跳台阶问题: f(0)=1 , f(1)=1 , f(2)=2。
斐波那契数列问题: f(0)=0 , f(1)=1 , f(2)=1 。
2.3、动态规划法
动态规划解析:
状态定义: 设 dp 为一维数组,其中 dp[i]的值代表 斐波那契数列第 i个数字 。
转移方程: dp[i + 1] = dp[i] + dp[i - 1],即对应数列定义 f(n + 1) = f(n) + f(n - 1);
初始状态: dp[0] = 1, dp[1] = 1 ,即初始化前两个数字;
返回值: dp[n],即斐波那契数列的第 n 个数字。
class Solution {
public:
int numWays(int n) {
if(n<2)
return 1;
int a=0,b=1,c=1;
for(int i=2;i<=n;i++)
{
a=b;
b=c;
c=(a+b)% 1000000007;
}
return c;
}
};
时间复杂度 O(N)。
空间复杂度 O(1)。
2.4、小结
像这种求多少种可能性的题目一般都有递推性质,优先考虑动态规划算法。
三、矩阵中的路径
3.1、题目描述
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
例如,在下面的 3×4 的矩阵中包含单词 “ABCCED”(单词中的字母已标出)。
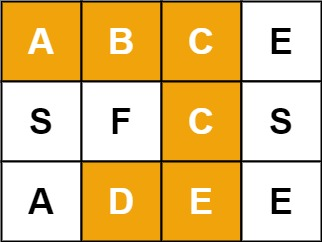
示例 1:
输入:board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出:true
示例 2:
输入:board = [[“a”,“b”],[“c”,“d”]], word = “abcd”
输出:false
来源:力扣(LeetCode)
3.2、思路
典型的矩阵搜索问题,可使用深度优先搜索(DFS)+ 回溯剪枝解决。
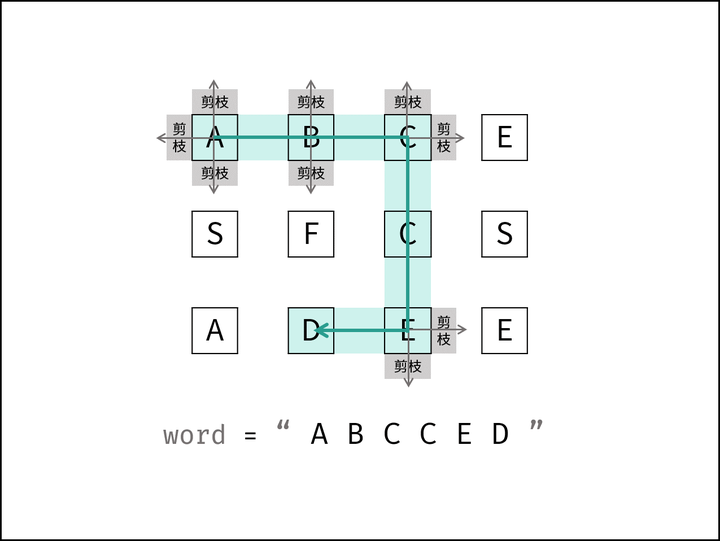
DFS递归参数:board数组及其行号 i 和列号 j ,word字符串及当前目标字符在word中的索引 k 。
DFS递归终止条件:
返回false:行号超出索引范围、列号超出索引范围、当前board的字符board[i][j]不等于目标字符word[k]。
返回true:字符串word已全部匹配,即k = len(word) - 1。
递推过程和防止错误:
- 标记当前矩阵元素: 将 board[i][j] 修改为空字符 ‘\0’,代表此元素已访问过,防止之后搜索时重复访问而出现错误。
- 朝当前元素的上、下、左、右四个方向开启下层递归,使用或连接 (代表只需找到一条可行路径就直接返回,不再做后续 DFS ),并记录结果。
- 还原当前矩阵元素, 将 board[i][j] 元素还原至初始值,即 word[k] 。为什么还原是word[k]?因为如果board[i][j] != word[k]就已经被终止递归返回false了,不会运行到下面。
3.3、代码实现
class Solution {
private:
int rows, cols,n;
bool dfs(vector<vector<char>>& board, string word,int i,int j,int k)
{
if(i<0 || j<0 || i>=rows || j>=cols || board[i][j]!=word[k])
return false;
if(k==n-1)
return true;
board[i][j]='\0';
bool ret=dfs(board,word,i,j-1,k+1) || dfs(board,word,i,j+1,k+1)
|| dfs(board,word,i-1,j,k+1) || dfs(board,word,i+1,j,k+1);
board[i][j]=word[k];
return ret;
}
public:
bool exist(vector<vector<char>>& board, string word) {
rows=board.size();
cols=board[0].size();
n=word.size();
for(int i=0;i<rows;i++)
{
for(int j=0;j<cols;j++)
{
if(dfs(board,word,i,j,0))
return true;
}
}
return false;
}
};
时间复杂度: O ( 3 K M N ) O(3^K MN) O(3KMN) 。最差情况下,需要遍历矩阵中长度为K字符串的所有方案,时间复杂度为 O ( 3 K ) O(3^K) O(3K) ;矩阵中共有MN个起点,时间复杂度为 O(MN) 。
空间复杂度O(K):搜索过程中的递归深度不超过K。
3.4、小结
矩阵搜索问题,可使用深度优先搜索(DFS)+ 回溯剪枝解决。只要理清楚这几点:
- 解决搜索时重复访问问题。
- 递归的中止条件,也叫剪枝。
- 递归的参数。
- 递归发散的方向。
总结
一定要做好总结,特别是当没有解出题来,没有思路的时候,一定要通过结束阶段的总结来反思犯了什么错误。解出来了也一定要总结题目的特点,题目中哪些要素是解出该题的关键。不做总结的话,花掉的时间所得到的收获通常只有 50% 左右。
在题目完成后,要特别注意总结此题最后是归纳到哪种类型中,它在这种类型中的独特之处是什么。