1引言

NSGA-II算法学习过程中涉及到了较多内容，除了遗传算法中，核心步骤选择、交叉、变异外，又融入了快速非支配排序、拥挤度计算等内容。

在GA中，选择通常采用轮盘赌选择策略，为了加快收敛保留全局最优解，在采用轮盘赌的同时，通常引入精英保留（精英策略）提升算法性能。对于交叉和变异，通常在原染色体上进行，生成子代染色后，直接替换掉原染色体。

在NSGA-II中，每次迭代过程中，为了保证多样性，探索解空间，选择（采用的锦标赛选择）、交叉和变异产生子代种群后不会进行替换。此时有原种群P，及选择交叉变异后得到子代种群Q，P、Q种群规模均为N，合并P和Q为2N的新种群R。精英策略则通过快速非支配排序、拥挤度计算保留种群R种的精英解，淘汰差解，得到新父代种群P’。

2多目标多旅行商问题

对于多目标多旅行商问题：

若旅行商数量不固定，相关文献¹有以min{f1=最小化旅行商数量，f2=各旅行商之间行驶距离平衡}为目标。求解方法为：采用聚类方法，采用聚类方法确定旅行商数量，转化为旅行商固定的情况，此时仅优化目标f2即可。由于采用了聚类方法，导致第一目标函数旅行商数量固定，无需再使用多目标算法。
若旅行商数量固定，有的文献²以min{f1=所有旅行商行驶距离之和最小，f2=各旅行商之间行驶距离平衡}。求解方法可采用智能优化算法，如NSGA-II，编码方式为两层编码（两部分编码）²，第一层编码为不包含分隔符的传统 TSP 问题遗传编码，第二层编码用于记录该方案中在何处分隔，1 个分隔符位表示有 2 个旅行商。详见第3章。

本文研究的场景为旅行商数量固定的情况。问题描述为：
𝑚个推销员从同一座中心城市出发，访问其中一定数量的城市并且每座城市只能被某一个推销员访问一次，最后返回到中心城市，通常这种问题模型被称之为单仓库多旅行商问题（Single-Depot Multiple Travelling Salesman Problem, SD-MTSP）；
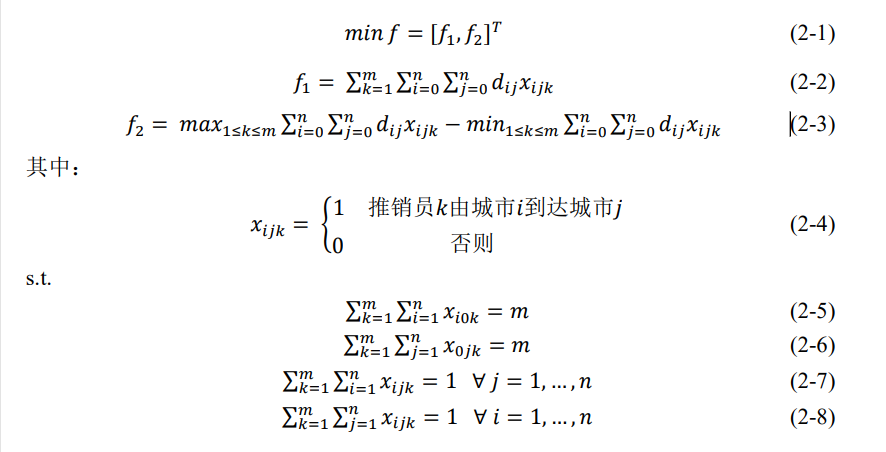
在这里插入图片描述
其中，等式(2-1)表示需要同时最小化两个目标函数。等式(2-2)表示所有推销员的总路程，等式(2-3)代表着推销员中最长路线与最短路线的差值（平衡度）。等式(2-5)与等式(2-6)的含义是编号为 0 的中心城市的入度和出度都必须为𝑚，即代表𝑚个推销员均从中心城市出发并且完成行程后都回到了中心城市。等式(2-7)与等式(2-8)则表示除中心城市外的其他所有城市的出度和入度均为 1，即每个城市能且只能被推销员中的一个人访问。

3多目标遗传算法NSGA-II

3.1 编码

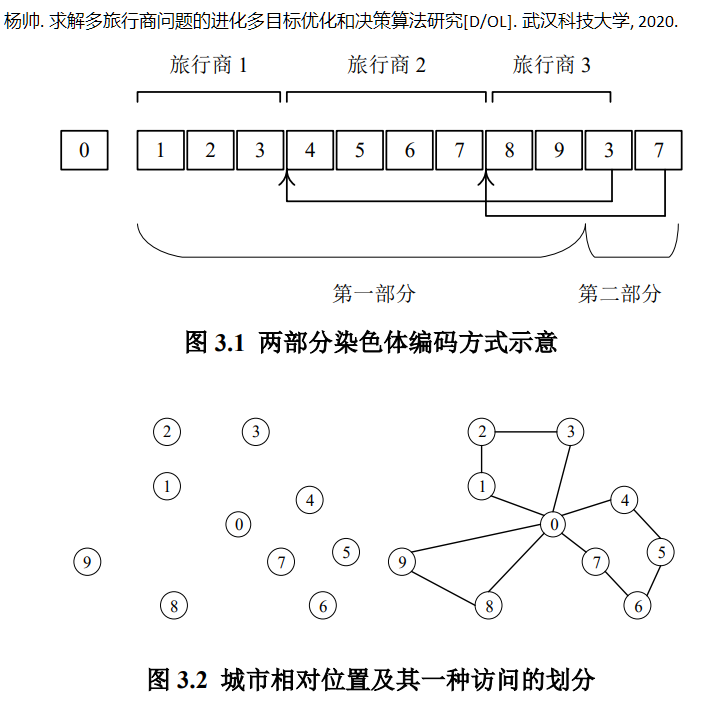
设一种多旅行商问题的城市个数是 10，推销员人数为 3，在编码的时候，将城市按照自然数 0,1,…,9 进行编号，其中 0 为中心城市，即所有推销员的起始和终止点。图 3.1 展示出了上述编码方式下的一种解方案，其中染色体上的第一部分为 10 个自然数的一种排列，而第二部分则将第一部分分割成了三份，分别表示三个推销员所需要拜访的城市，其排列顺序就是拜访顺序，即三个推销员的路径分别为：0->1->2->3->0，0->4->5->6->7->0，0->8->9->0。设城市的位置关系如图 3.2
左所示，则图 3.1 的个体所代表的解如图 3.2 右所示。
在这里插入图片描述

3.2选择（锦标赛选择）

锦标赛方法选择策略每次从种群中取出一定数量个体（放回抽样），然后选择其中最好的一个进入子代种群。重复该操作，直到新的种群规模达到原来的种群规模。具体的操作步骤如下：

确定每次选择的个体数量。一般选择2个（二元锦标赛）。
从种群中随机选择个个体(每个个体入选概率相同) 构成组，根据每个个体的适应度值，选择其中适应度值最好的个体进入子代种群。
重复步骤2，得到的个体构成新一代种群。

3.3 交叉（顺序交叉）

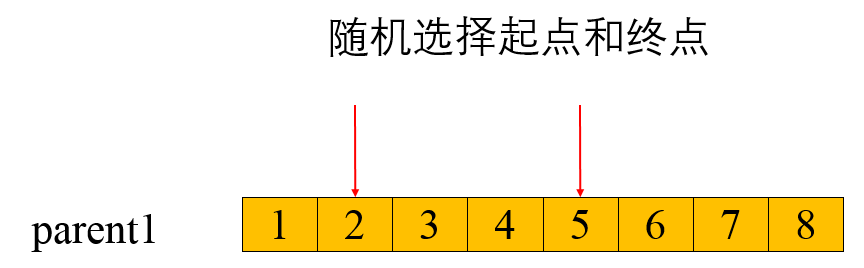
采用顺序交叉³，本文编码为两部分编码，对第一部分进行顺序交叉，第二部分保持不变。在两个父代染色体中随机选择起始和结束位置，将父代染色体1该区域内的基因复制到子代1相同位置上，再在父代染色体2上将子代1中缺少的基因按照顺序填入。具体步骤如下：

随机选择一对染色体（父代）中几个基因的起止位置（两染色体被选位置相同）。
生成一个子代，并保证子代中被选中的基因的位置与父代相同。
先找出第一步选中的基因在另一个父代中的位置，再将其余基因按顺序放入上一步生成的子代中。

3.4 变异

采用2-opt作为变异方式，只对第一部分。

3.5快速非支配排序

3.5.1符号说明

支配计数 $n_p$ ，即支配解p的解的数量。
Sp：解p支配的解的集合。
P种群，p个体索引
$F_i$ 第i层非支配解集
p_{rank}个体p的帕累托层级

3.5.2快速非支配排序⁴⁵

3.5.3快速非支配排序举例⁶

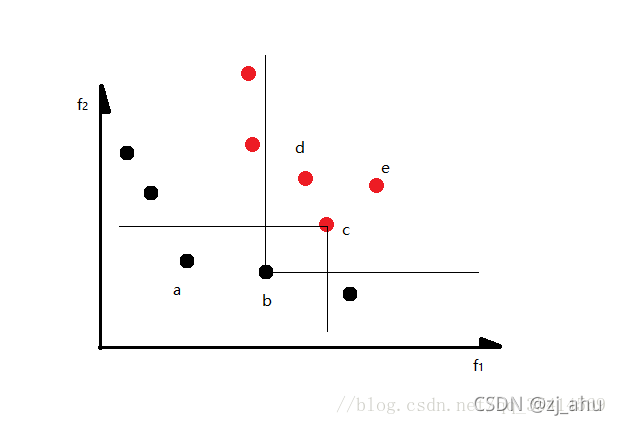
最小化双目标问题，如上图所示，对解c而言，解c被a,b两个解支配，所以 $n_c$ 为2。对解b而言，解b支配c,d,e，所以 $S_b=\{c,d,e\}$ 。

3.6拥挤比较算子

密度估计：对同一前沿面的解按照目标函数值排序，计算每个解在该目标函数下两侧解的目标函数归一化差值，然后将所有目标函数下的分量累加作为拥挤系数。
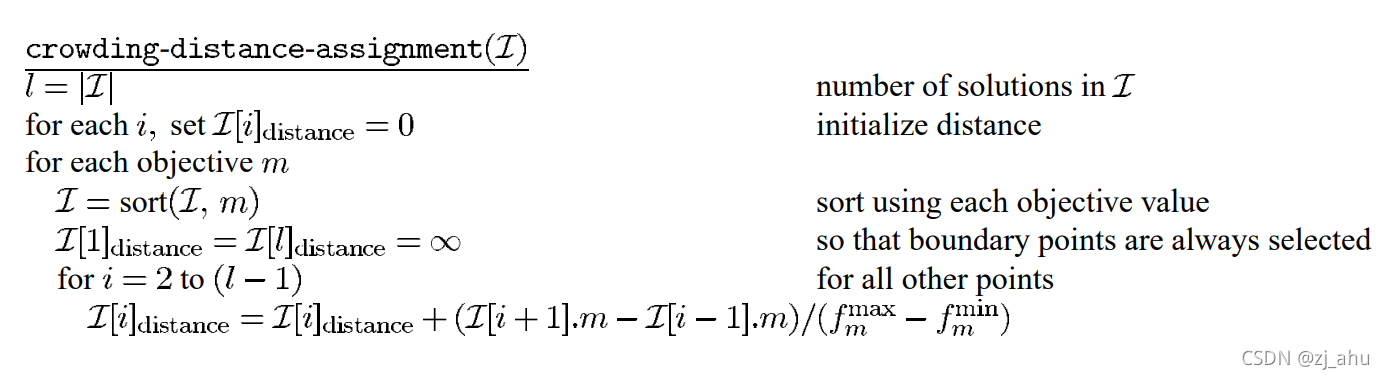
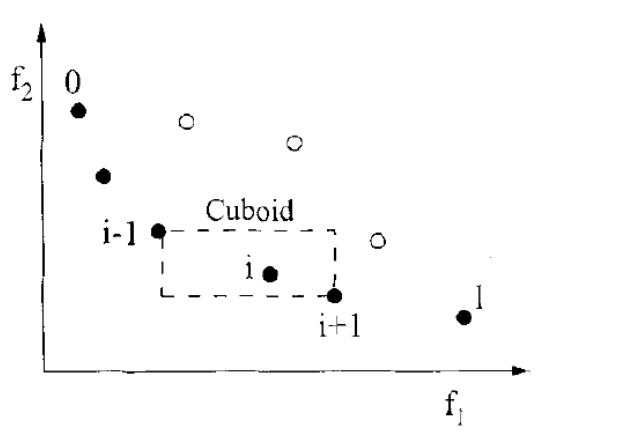
在这里插入图片描述
从几何角度理解拥挤距离，以两个目标函数为例，下图中黑点和白点分别为两个非支配前沿，对于解 $i$ ，从与 $i$ 在同一非支配前沿中选择与解 $i$ 最相近的两个点 $i - 1$ 和 $i + 1$ 为顶点组成一个长方形(cuboid)，拥挤距离即为长方形周长。
在这里插入图片描述

3.7精英策略

精英保留策略，核心思想是把群体在进化过程中迄今出现的最好个体不进行遗传操作而直接复制到下一代中，理论上证明了具有精英保留的标准遗传算法是全局收敛的，具体步骤如下：

将父代种群P和子代种群Q合并，组成种群规模大小为2N的新种群R。
将R进行非支配排序，并计算每个个体的拥挤度。
将非支配排序得到的非支配集F1，放到新父代种群P’中。若此时此时P’种群规模<N，则继续添加非支配集F2。当种群规模超出N时，则采用拥挤度比较算子添加个体至P $^\prime$ ，使P $^\prime$ 种群规模达到N。

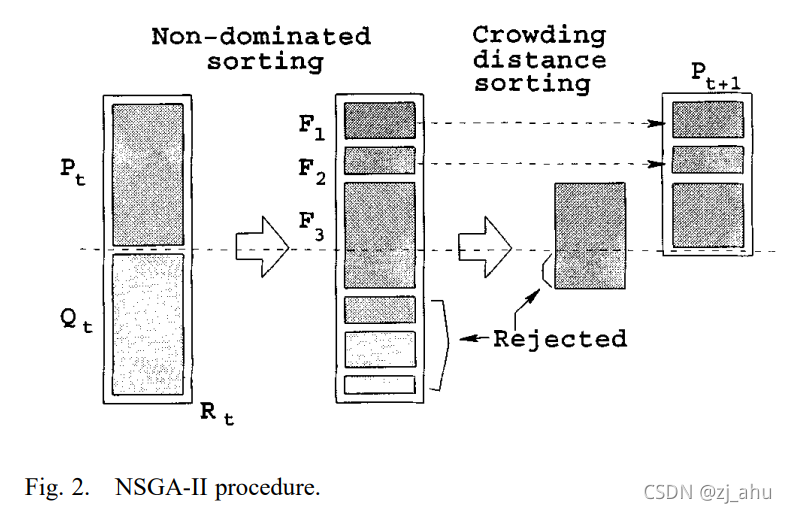
在这里插入图片描述

3.8 NSGA-II算法流程

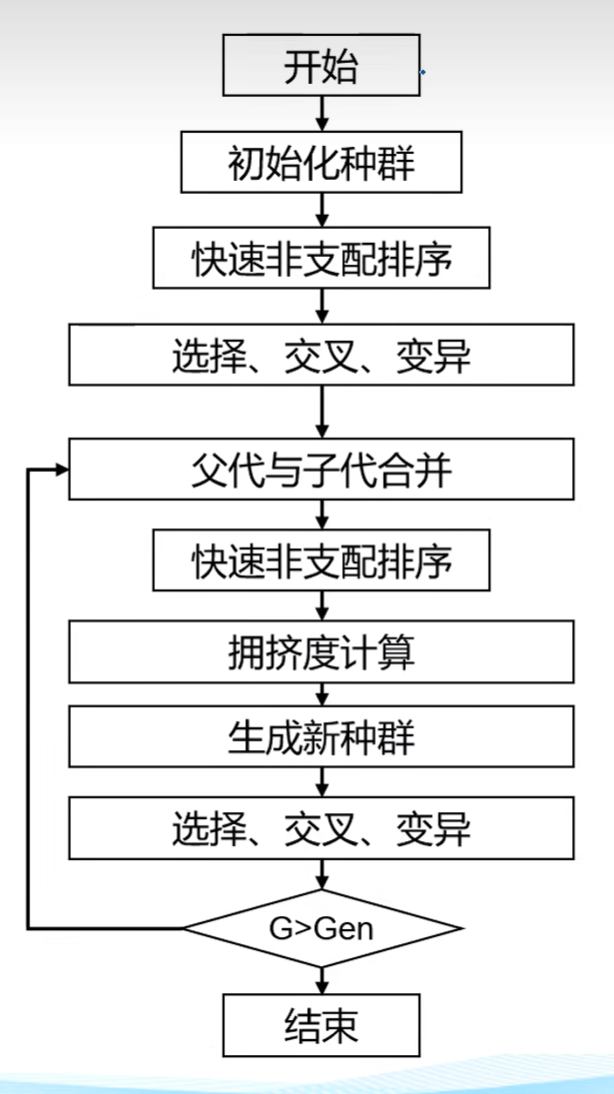
step1：初始化种群P，设置最大迭代次数G，令当前迭代次数g=1。
step2：计算目标函数值，进行快速非支配排序。
step3：对P进行选择、交叉、变异，生成子代种群Q。
step4：合并P和Q得到R，对R进行快速非支配排序，拥挤度计算，生成P’。【精英选择策略】
step5：对新父代种群进行选择(只采用锦标赛选择方法⁷ ，基于序值和拥挤度距离进行选择)、交叉、变异，生成新子代种群Q’，令P:=P’，Q:=Q’。
step6：判断G>g?，是则转step4；否则结束。

参考

胡士娟,鲁海燕,向蕾等.求解MMTSP的模糊聚类单亲遗传算法[J].计算机科学,2020,47(06):219-224. ↩︎
杨帅. 求解多旅行商问题的进化多目标优化和决策算法研究[D/OL]. 武汉科技大学, 2020. https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&dbname=CMFD202101&filename=1020105561.nh&v=. ↩︎ ↩︎
遗传算法一些交叉算子 ↩︎
NNSGA-II:快速精英多目标遗传算法（论文+代码解读） ↩︎
NSGA II算法详解 ↩︎
多目标优化经典算法——NSGA-II ↩︎
韩亚星. B2B模式下果蔬产品同城配送路径优化研究[D/OL]. 大连海事大学, 2019. https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&dbname=CMFD202001&filename=1020016871.nh&v=. ↩︎