目录

线性回归算法

求导法推导

梯度下降法推导

线性回归实现人脸识别

导入数据

构建标签矩阵

经典线性回归求导法实现

经典线性回归梯度下降法实现

岭回归实现

套索回归实现

局部加权线性回归实现

可视化

人脸识别

---

线性回归算法

求导法推导

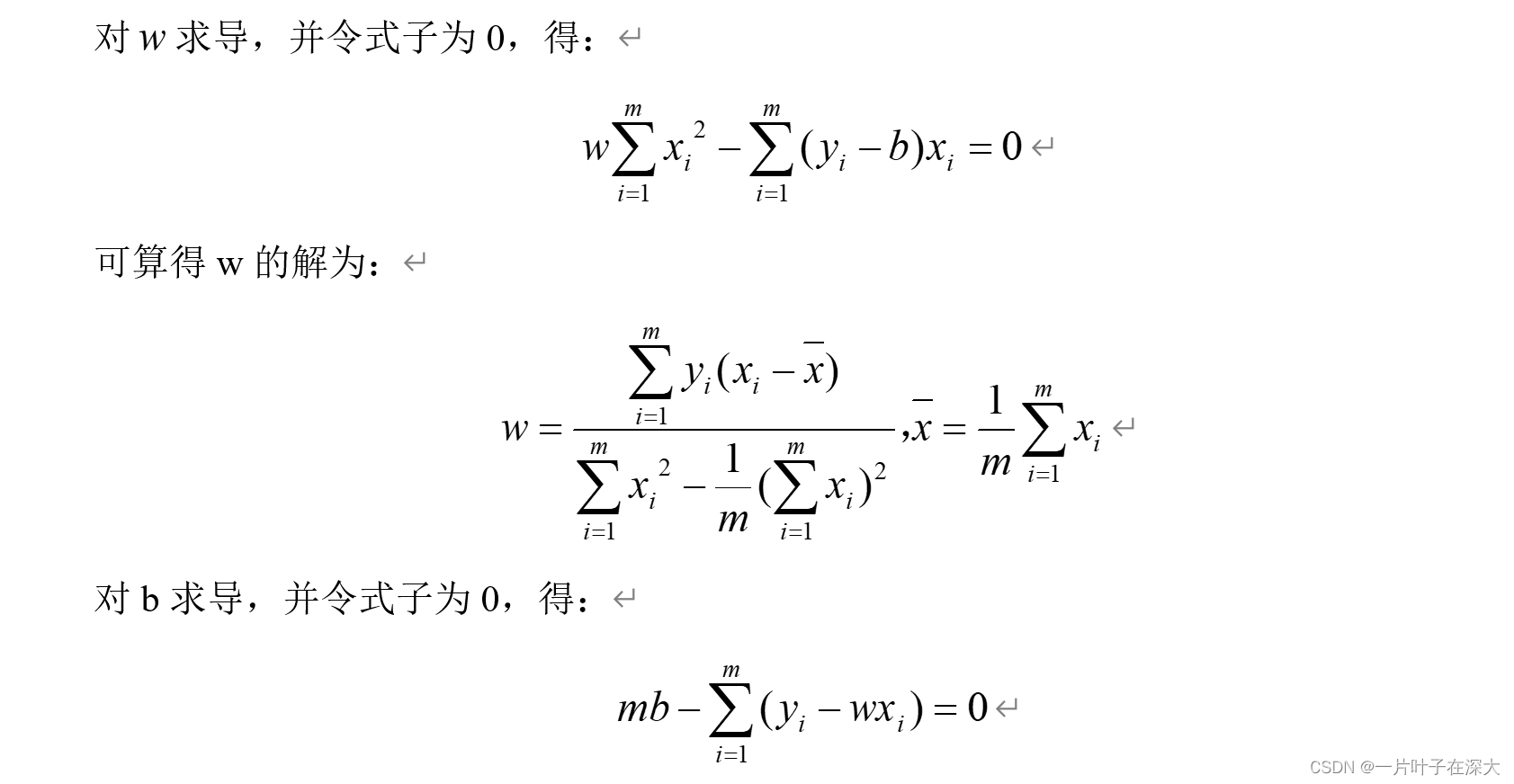
梯度下降法推导

线性回归实现人脸识别

导入数据

% pictures=dir('C:\Users\Yezi\Desktop\机器学习\AR_Gray_50by40\*.tif');
people=10;
personPictureNumber=100;
sample=[];
pictureNumber=people*personPictureNumber;
testData=[];
trainData=[];
testNumber=50;
trainNumber=personPictureNumber-testNumber;
testDataNumber=testNumber*people;
trainDataNumber=trainNumber*people;
dimension=16*16;
for i=1:pictureNumber
%     picture=imread("C:\Users\Yezi\Desktop\机器学习\AR_Gray_50by40\"+pictures(i).name);
%     picture=double(picture);
%     picture=picture(:);
    picture=usps1000(:,i);
    sample=[sample,picture];
    if mod(i,personPictureNumber)<trainNumber+1 && mod(i,personPictureNumber)~=0
        trainData=[trainData,picture];
    else
        testData=[testData,picture];
    end
end

构建标签矩阵

标签矩阵是这样一个矩阵：对应类别的位置为1，其他位置为0，例如，数字1对应0100000000，数字0对应1000000000，数字3对应0010000000。

Y=zeros(people,trainDataNumber);
for i=1:trainDataNumber
    Y(floor((i-1)/trainNumber)+1,i)=1;
end

经典线性回归求导法实现

求导法直接代入解的公式即可。

 W就是模型的参数。

W=pinv(trainData*trainData')*trainData*Y';

经典线性回归梯度下降法实现

①数据预处理：首先，通过计算训练数据每列（特征）的均值和标准差，对训练数据进行标准化处理，即将每个特征的值减去其均值，然后除以标准差。这样做是为了确保不同特征具有相似的尺度，有助于梯度下降算法的收敛。

②初始化权重参数：创建一个大小为dimension × people的全零矩阵W，用于存储线性回归模型的权重参数。

③设置学习率：将学习率a设置为一个较小的值，用于控制每次更新权重的步长。

④利用梯度下降法更新权重：通过迭代的方式，多次更新权重参数W，直到达到指定的迭代次数。在每次迭代中，根据当前的权重W、训练数据trainData和标签矩阵Y，计算出一个临时的权重参数WTemp。这里使用了线性回归的梯度下降法更新公式。具体来说，根据模型的误差（即预测值与实际值的差）和梯度信息，按照一定的步长反向调整权重的值。

⑤保存最终的权重参数：将最后一轮迭代得到的临时权重参数WTemp赋给变量W，得到最终的权重参数。

for i=1:trainDataNumber
    meanmean=mean(trainData(:,i));
    stdstd=std(trainData(:,i));
    for j=1:dimension
        trainData(j,i)=(trainData(j,i)-meanmean)/stdstd;
    end
end
for i=1:testDataNumber
    meanmean=mean(testData(:,i));
    stdstd=std(testData(:,i));
    for j=1:dimension
        testData(j,i)=(testData(j,i)-meanmean)/stdstd;
    end
end
W=zeros(dimension,people);
a=0.000001;
WTemp=W-2*a*trainData*(trainData'*W-Y');
for i=1:1000
    W=WTemp;
    WTemp=W-2*a*trainData*(trainData'*W-Y');
end
W=WTemp;

岭回归实现

岭回归（Ridge Regression）是一种用于处理线性回归问题的方法，它通过引入正则化项来改善模型的稳定性和预测能力。

在线性回归中，当存在多个特征时，可能会出现过拟合（overfitting）的问题，即模型在训练数据上表现良好，但在新样本上的泛化能力较差。过拟合通常发生在特征间存在高度相关性或特征维度较高的情况下。

岭回归通过添加一个正则化项到线性回归的损失函数中，可以有效地缓解过拟合问题。这个正则化项是模型权重平方的乘子，将其加到损失函数中，限制了权重的增长。正则化项的大小由超参数λ（lambda）控制，λ越大，则正则化影响越大。

岭回归的优点是可以减少模型对数据中噪声的敏感性，并改善预测的稳定性。通过惩罚权重的增长，岭回归可以有效地解决特征共线性（collinearity）问题，即特征之间强相关的情况。

使用岭回归的步骤包括选择合适的超参数λ，然后对模型进行训练和预测。通过调整λ的值，可以在模型的偏差（bias）和方差（variance）之间进行权衡，以获得最佳的预测性能。

W=(trainData*trainData'+eye(dimension)*4500000)^-1*trainData*Y';

套索回归实现

套索回归（Lasso Regression）是一种用于特征选择和线性回归问题的方法，它通过引入正则化项来改善模型的稳定性，并具备特征选择的能力。

与岭回归类似，套索回归也是在线性回归的基础上添加了正则化项。不同的是，套索回归使用的正则化项是模型权重的绝对值之和，而不是平方和。这使得套索回归具有一个特殊的性质，即可以将某些特征的权重压缩到零，从而实现特征选择的效果。

套索回归通过最小化损失函数和正则化项的和，来求解最佳的模型参数。其中，正则化项中的超参数α（alpha）控制着正则化的强度。较大的α值会导致更多的特征权重被压缩到零，从而进行更严格的特征选择。

套索回归的主要优点是可以产生稀疏解，即具备自动进行特征选择的能力。通过将一些特征的权重设为零，套索回归可以剔除模型中不重要或冗余的特征，提高模型的解释性和泛化能力。

使用套索回归的步骤与岭回归类似，需要选择合适的超参数α，并进行模型训练和预测。通过调整α的值，可以在模型的偏差和方差之间进行权衡，获得最佳的预测性能和特征选择结果。

for i=1:trainDataNumber
    meanmean=mean(trainData(:,i));
    stdstd=std(trainData(:,i));
    for j=1:dimension
        trainData(j,i)=(trainData(j,i)-meanmean)/stdstd;
    end
end
for i=1:testDataNumber
    meanmean=mean(testData(:,i));
    stdstd=std(testData(:,i));
    for j=1:dimension
        testData(j,i)=(testData(j,i)-meanmean)/stdstd;
    end
end
W=zeros(dimension,people);
for i=1:people
    w=lasso(trainData',Y(i,:));
    W(:,i)=sum(w,2);
end

局部加权线性回归实现

局部加权线性回归（Locally Weighted Linear Regression，LWLR）是一种非参数的回归方法，它在进行预测时使用了局部加权的策略，根据样本的相似度为每个数据点赋予不同的权重。

在传统的线性回归中，我们试图拟合一个全局性的线性模型，即假设所有数据都遵循同一个线性关系。然而，在某些情况下，数据可能呈现出明显的非线性特征或包含离群点，此时全局线性模型可能无法很好地拟合数据。

局部加权线性回归通过为每个数据点赋予一个权重，使得在预测时更加关注附近数据点的贡献。具体而言，对于待预测点，LWLR会给予距离该点较近的训练样本较高的权重，而对于距离该点较远的样本，则赋予较低的权重甚至可以忽略。这样做的目的是使预测点附近的样本对模型拟合产生更大的影响，从而实现对数据局部的拟合。

LWLR的拟合过程与传统的线性回归类似，但在计算参数时需要考虑每个数据点的权重。通常使用高斯核函数来计算权重，根据距离待预测点的远近决定权重的大小。然后，通过加权最小二乘法来拟合局部加权的线性模型。

LWLR的优点是能够更好地拟合非线性关系和处理离群点。它能够根据数据的特点自适应地调整模型，使得预测结果更加准确。但是，LWLR也存在一些缺点，比如计算量较大，对训练数据的依赖性较强，并且在高维数据上可能出现过拟合的问题。

w=zeros(trainDataNumber);
for i=1:trainDataNumber
    x=mod(i-1,trainNumber);
    w(i,i)=i/sqrt(2*pi)*exp(-x*x/2);
end
W=pinv(trainData*w*trainData')*trainData*w*Y';

可视化

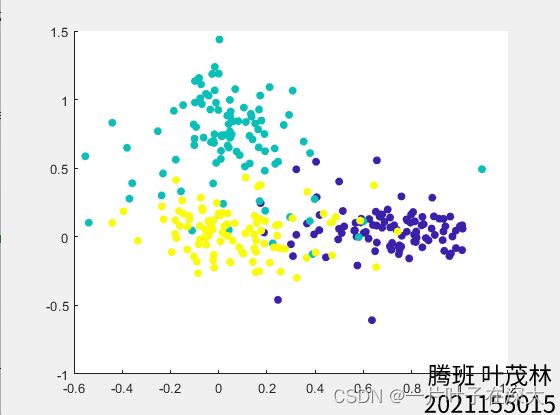
visualizeDataTemp=[];
%3个人
for i=0:2
    visualizeDataTemp=[visualizeDataTemp,sample(:,i*personPictureNumber+1:i*personPictureNumber+personPictureNumber)];
end
egienvector=W(:,1:2);
visualizeData=egienvector'*visualizeDataTemp;
colors=[];
for i=1:3*personPictureNumber
    color=floor((i-1)/personPictureNumber+1)*50;
    colors=[colors,color];
end
scatter(visualizeData(1,:),visualizeData(2,:),[],colors,'filled');

人脸识别

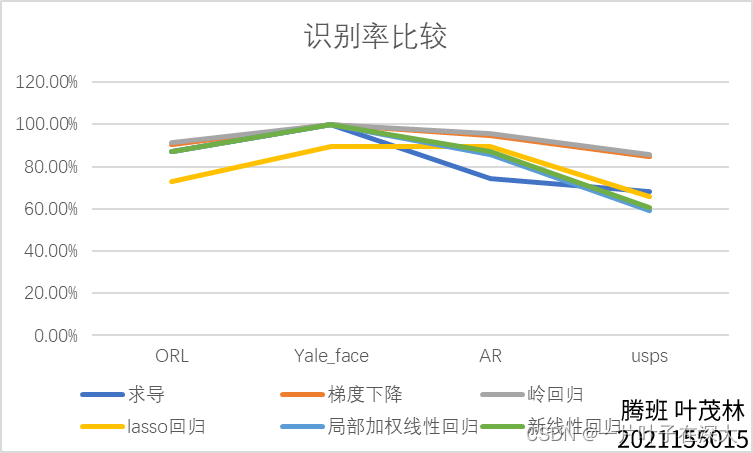
这个人脸识别率就好算了，直接数有多少个是算对的就行。 

Predict=W'*testData;
[~,Index]=sort(Predict,'descend');
right=0;
for i=1:testDataNumber
    if Index(1,i)==floor((i-1)/testNumber)+1
        right=right+1;
    end
end
result=right/(testDataNumber);