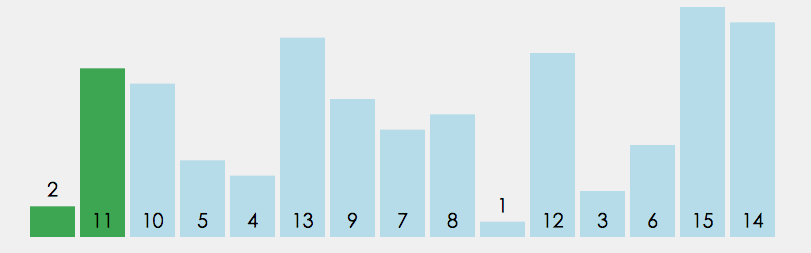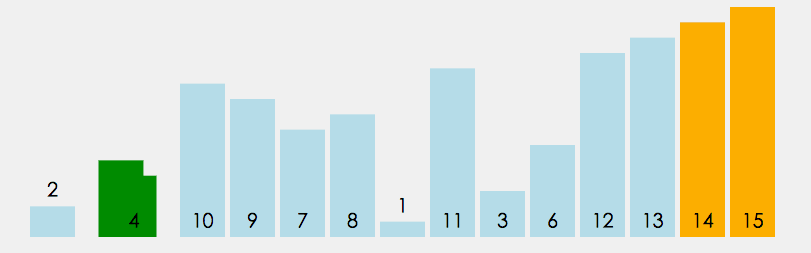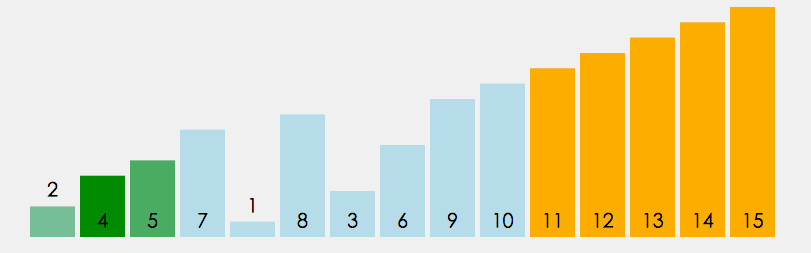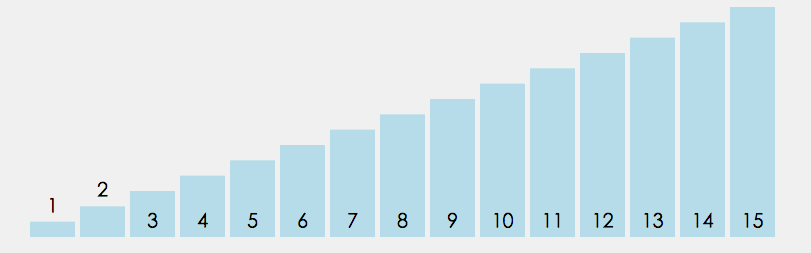目录
前言:
动态规划:
常见应用:
解题步骤:
动态规划的简化步骤:
案例:
509. 斐波那契数 - 力扣(LeetCode)
70. 爬楼梯 - 力扣(LeetCode)
62. 不同路径 - 力扣(LeetCode)
总结:
前言:
本文我们将为大家讲解一下动态规划的理论知识,并且会讲解几道力扣的经典例题。各位如果感兴趣可以点击进来阅读。
动态规划:
动态规划是一种解决问题的数学思想和算法。它通常用于解决优化问题,即在一系列决策中找到最优解。动态规划的关键是将问题划分为子问题并进行递推求解。实际上,动态规划可以看作是将大问题划分为更小的,重复的子问题的解决方法,通过存储子问题的解并重复使用它们来减少计算。因此动态规划中经常会用到记忆化搜索或状态压缩。
记忆化搜索是一种优化搜索的方法,通过对已经计算过的结果进行存储和重复使用,避免重复的计算。递归的过程中,对于每一个计算子问题的过程,将其结果存储下来,同时若下一次计算相同的子问题,则直接从存储中取出结果,避免了重复的计算过程。记忆化搜索算法常用于动态规划,可以提高算法的效率,避免运算时间复杂度的爆炸性增长。
状态压缩通常用于离散化的问题中,将问题中的某个状态按照一定的规则进行编码,转换成一个整数或者一个二进制数,以便在算法运算中更快速、简洁地处理这些状态。状态压缩通常用于位运算、哈希表,或者开数组等数据结构上,其优点是占用的空间小、时间复杂度低。在某些场景下,通过状态压缩,可以将时间复杂度降低到O(1)的级别。常见的状态压缩的应用包括华容道、八皇后、数独、迷宫等。
常见应用:
动态规划是一种思想和方法,可以应用于很多问题。以下是常见的动态规划应用:
1. 背包问题:将不同重量和价值的物品装入一个背包中,使得背包中的物品总价值最大。
2. 最长公共子序列问题:找出两个字符串中最长的公共子序列,即两个字符串中都有的最长子序列。
3. 最短路径问题:在有向图中找出从源节点到终节点的最短路径,通常使用迪杰斯特拉算法和贝尔曼-福德算法等。
迪杰斯特拉算法和贝尔曼-福德算法都是解决最短路径问题的算法,但它们的实现和应用领域略有不同。
迪杰斯特拉算法是一种单源最短路径算法,用于解决只有一个起点的有向图或无向图中,从起点到其他所有节点的最短路径问题。迪杰斯特拉算法的基本思想是不断更新起点到图中其他各节点的距离,并选择最短路径进行扩展,直到所有节点已经更新为止,最终得到起点到其它所有节点的最短路径。由于迪杰斯特拉算法中有很多重复计算和不必要的比较,通常采用优先队列等数据结构优化算法性能。
贝尔曼-福德算法是一种多源最短路径算法,可以解决具有负边权的有向图或无向图中的最短路径问题,但不支持负环图。贝尔曼-福德算法的基本思路是通过松弛操作,不断更新每条边连接的节点之间的最短路径长度。在算法迭代的过程中,对于每条边的更新,都要对所有边进行一遍松弛操作。直到更新次数达到最大允许的次数或不存在负环路为止,最终得到所有节点之间的最短路径。相比于迪杰斯特拉算法,贝尔曼-福德算法适用范围更广,但时间复杂度较高。
在图论中,松弛操作是指通过放宽约束条件来尝试更新节点之间的最短距离。松弛操作通常用于解决最短路径问题
总之,迪杰斯特拉算法和贝尔曼-福德算法都是解决最短路径问题的重要算法,可以根据具体问题的特点选择相应的算法加以运用。
4. 切割钢管问题:将一条长度为n的钢棒切割成若干段,每段长度为整数,求切割方案使得切割后的钢管价值最大。
5. 找零钱问题:给定不同面额的硬币,求将钱数为n的钱凑成指定的金额所需的最小硬币数。
6. 矩阵链乘法问题:在许多矩阵中把它们相乘,求完成乘法所需的最小数目的基本乘法操作次数。
7. 字符串编辑问题:计算将一个字符串转换成另一个字符串所需的最小操作(插入、删除、替换)次数。
8.股票买卖问题:如何操作自己的股票才能获得最大利益。
这就是动态规划的主要题型,我们实际上也只需要掌握这些题型就够了,足够应对大厂的面试以及各种动态规划竞赛题目。
解题步骤:
动态规划是一种求解最优化问题的算法思想,通常包括以下几个步骤:
1. 确定状态及其含义:根据问题的特点,确定状态及其含义,状态是动态规划算法的核心,从而建立与子问题之间的关系。
2. 确定状态转移方程:根据前一步确定的状态,找到各个阶段之间的联系,推导出状态转移方程,即当前状态与前一个状态之间的关系,这是求解最优解的关键。
3. 确定初始值:将问题转化为分阶段决策问题,并根据问题的实际情况确定初始状态值,准备迭代求解过程。
4. 迭代求解:根据状态转移方程,通过迭代计算,求解出所有子问题的最优解,进而得到问题的最优解。
5. 优化空间复杂度:在求解过程中,考虑压缩状态空间,减少存储需要从而达到优化空间复杂度的效果。这是优化算法的重要手段。
在实际应用中,以上步骤并不是一定需要全部按照顺序执行的,有时可以根据问题的情况先确定某些状态,再迭代求解,避免状态数量过多造成的时间和空间开销。
而动态规划的精髓就在于确定状态转移方程,以及利用状态转移方程确定DP数组。
在动态规划中,DP数组表示存储中间状态的一维或多维数组,也称为状态转移表或者状态转移矩阵。DP数组的作用是记录计算过程中的结果,以便于之后的计算。
在动态规划算法中,通常需要根据问题中定义的状态转移方程,将问题划分成一个个小问题,并计算出每个子问题的结果,将这些结果存储在DP数组中。之后,根据这些子问题的结果,通过状态转移方程计算出问题的最终结果。
DP数组的维度和含义通常由问题的性质和状态转移方程所决定。例如,对于背包问题,DP数组通常为二维数组,其中第一维表示物品个数,第二维表示背包容量,DP数组中的每个元素表示在前i个物品中,填满当前容量为j的背包时,所获得的最大价值。
需要注意的是,DP数组的存储空间通常比较大,特别是在处理大规模问题时。因此,在实际应用中,需要根据问题的实际情况,采取合理的优化措施,如状态压缩等,以减少存储空间的占用和算法的时间复杂度。
动态规划的简化步骤:
1.DP数组的含义以及下标的含义。
2.递推公式的推导。
3.DP数组的初始化。
4.DP数组遍历遍历顺序(背包问题)
其实整个动态规划的类型题,都可以按照这五步来确定出最终代码。
我们接下来通过例题来带大家学习什么是动态规划。
案例:
509. 斐波那契数 - 力扣(LeetCode)
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1

我们如果按照动态规划的思路来做:
1.DP数组的含义以及下标含义:此时 DP[i] 表示的是第i个数字的 斐波那契数 。
2.确定递推公式:这里题目已经直接给出F(n)=F(n-1)+F(n-2)
3.DP数组的初始化:题目已经给出F(0)=0,F(1)=1。
4.遍历顺序:因为我们要知道第n个数字的 斐波那契数,就要知道第(n-1)和第(n-2)个数字的 斐波那契数,因此我们这道题的遍历顺序采取从前往后进行遍历。
那我们已经知道了递推公式以及DP数组含义以及遍历,直接写代码就可以。
class Solution {
public:
int fib(int n) {
int nums[31];
nums[0]=0;
nums[1]=1;
for(int i=2;i<=n;i++)
{
nums[i]=nums[i-1]+nums[i-2];
}
return nums[n];
}
};这道题属于动态规划的最基础入门题目,他向我们揭示了动态规划的最基础解题思路。
70. 爬楼梯 - 力扣(LeetCode)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
我们按照动态规划的思路来做:
1.DP数组的下标及其含义:nums[i] 表示 到达第 i 阶台阶的方法数
2.确定递推公式:
网上太多只讲理论不讲为什么,我们在这里手推一下为什么第n阶台阶的走法是第(n-1)阶台阶的走法加上第(n-2)阶台阶的走法,(我们以第五阶台阶为例)
第一阶 :1
第二阶 :11 2
第三阶:111 12 21
此时要想直接到第五阶台阶需要走两步(直接在第三阶的方法上加2)
1112,122,212
第四阶:112 22 1111 122 211
此时想到第五阶台阶需要走一步(直接在第四阶的方法上加1)
1121 221 11111 1221 21111
我们可以发现其实第五步全是第三阶和第四阶走法变种。
其实这道题唯一一个比较绕的是:很多同学不理解为什么我们到达num[i-1]或num[i-2]之后,不是还要再往前走一步或者两步嘛?为什么就可以不要这一两步呢?
其实就是因为我们这道题要的是方法,不是步数。而我们自己规定了只能走一步或者两步后,假设我们此时到达num[i-2]之后,其实方法就已经固定了,因为我们接下来只能往向前走两步(如果走一步那就与nums[i-1]重合了)。是不可能再产生新方法的,num[i-1]同理.因此我们判断出递推公式为:nums[i]=nums[i-1]+nums[i-2]。
3.DP数组的初始化:num[1]=1.nums[2]=2。很通俗易懂的初始化。
4.遍历顺序:由本题的公式nums[i]=nums[i-1]+nums[i-2] 就可以知道这道题的遍历顺序需要是从前往后。
通过这个思路我们也可以快速写出本题代码。
class Solution {
public:
int climbStairs(int n) {
int nums[46];
nums[0]=0;
nums[1]=1;
nums[2]=2;
for(int i=3;i<=n;i++)
{
nums[i]=nums[i-1]+nums[i-2];
}
return nums[n];
}
};62. 不同路径 - 力扣(LeetCode)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
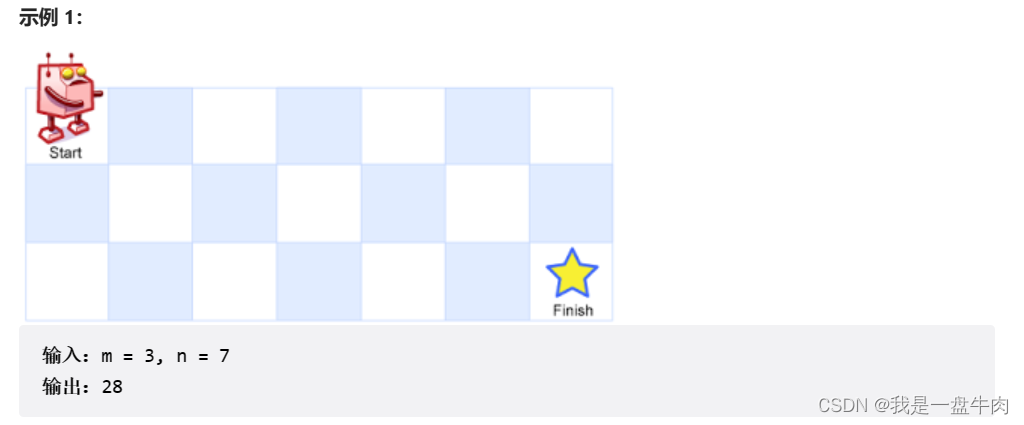
这道题就属于进阶的动态规划题目,这道题的最基本思路就是我们记录这个机器人从起点开始到每一个格子的不同路径条数,这样不断的推,就可以推出到达finish的不同路径数。
我们按照动态规划的思路来做:
1.DP数组的含义以及下标含义:nums[i][j] 表示机器人从 起点 开始到 nums[i][j] 的不同路径条数
2.确定递推公式:因为机器人只能是向下或者向右走,那么num[i][j] = nums[i-1][j] + nums[i][j-1].
3.DP数组的初始化:这个题初始化这里也是比较绕的:我们只能向下或者向右移动,那么我们就需要知道向下移动时本格的路径数以及向右移动时本格的路径数。
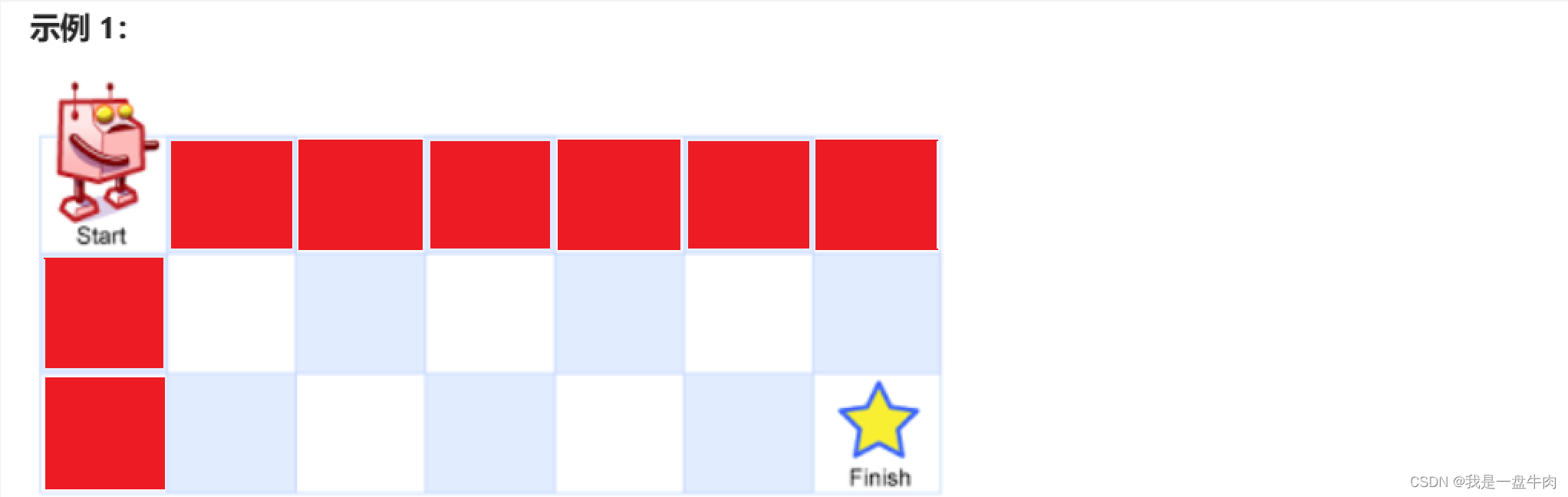
也就是说标红色的格子一定要进行初始化,否则你想向左或者向右移动的时候无法利用递推公式。
而正因为它只能向下或向右移动,也就是说标红色的这些各种路径数都只有一条,也就是只能向右或者向下走
4.遍历顺序:那我们此时只需要挨个遍历这些未标红的格子不就好了。
那我们已经知道了递推公式以及DP数组含义以及遍历,直接写代码就可以。
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> nums(m, vector<int>(n, 0));
for(int i=0;i<m;i++)
{
nums[i][0]=1;
}
for(int j=0;j<n;j++)
{
nums[0][j]=1;
}
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
nums[i][j]=nums[i-1][j]+nums[i][j-1];
}
}
return nums[m-1][n-1];
}
};总结:
关于动态规划的理论知识以及案例讲解我们就到这里,相应的刷题篇也会更新在leetcode合集里面,并且比较重要的背包问题我们会单独出一篇进行讲解的,各位同学如果感兴趣可以订阅该专栏,跟着我一起学透算法,让我们一起加油吧!
如果我的内容对你有帮助,请点赞,评论,收藏。创作不易,大家的支持就是我坚持下去的动力!